牛客多校第四场 C Chiaki Sequence Reloaded（数位dp）

链接：https://www.nowcoder.com/acm/contest/142/C
来源：牛客网
 

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 131072K，其他语言262144K
64bit IO Format: %lld

题目描述

Chiaki is interested in an infinite sequence a1, a2, a3, ..., which defined as follows:

Chiaki would like to know the sum of the first n terms of the sequence, i.e. . As this number may be very large, Chiaki is only interested in its remainder modulo (109 + 7).

输入描述:

There are multiple test cases. The first line of input contains an integer T (1 ≤ T ≤ 105), indicating the number of test cases. For each test case:
The first line contains an integer n (1 ≤ n ≤ 1018).

输出描述:

For each test case, output an integer denoting the answer.

示例1

输入

复制

10
1
2
3
4
5
6
7
8
9
10

输出

复制

0
1
2
2
4
4
6
7
8
11

【总结】

这题应该是今天收获最大的一题，数位dp一直不怎么会用，一边畏惧着一边敲着。代码写好了，debug一小时，比赛结束。。。。你一定能体会到把变量名弄混了，debug的痛苦。

大型dp（大佬们的小型dp）没经验不好写啊。

【分析】

设 ，前几项就是：1,3,6,10,15,21,........不难发现，每四项一个周期，每个周期前两项为奇数，后两项为偶数

那么对于就与S(n)的奇偶性有关了，也就是说，当n%4等于1或2时，是 -1，反之为1

往二进制上靠拢，也就是当n的二进制末尾两位是01或10时，是 -1，反之为1

 

再来看数列a的通项公式(n>=2时)：

   (a1可以省略)

现在，就完全可以只在意S(i)的二进制末两位是不是01或10了，是则-1，否则+1，就是a(n)的值。

例如：十进制10等于二进制1010，所以a(1010) = S(1010)+S(101)+S(10)，所以只需判断1010的所有相邻两位，有多少01或10，即为S()值为-1，剩下的就是1

 

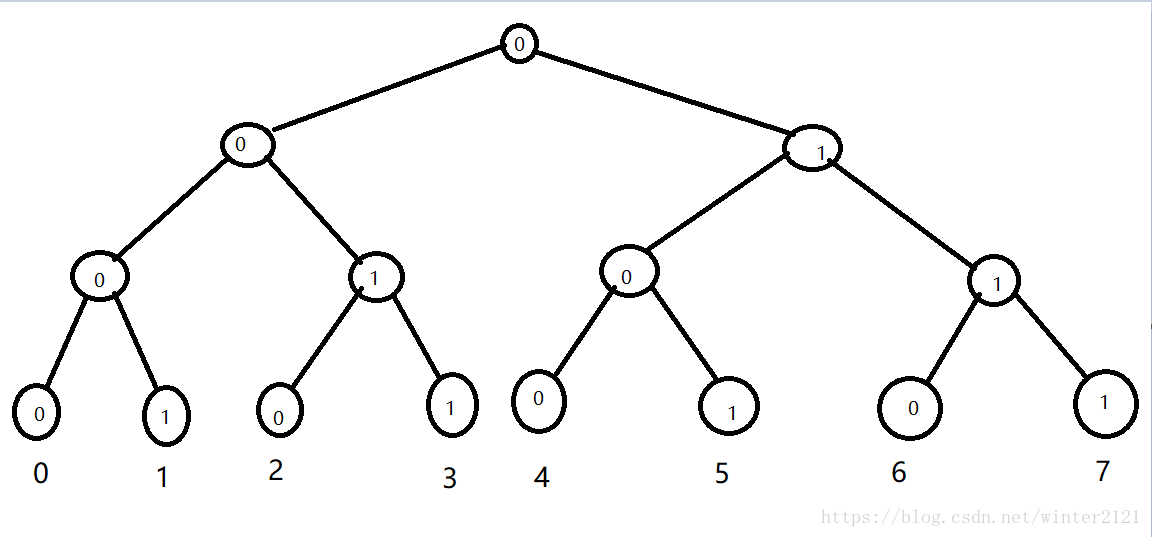
请以完全二叉树的思路思考下面

例如询问a5的值，就是根结点到叶子结点5路径上，第一次遇到1结点开始统计，01或10的数量表示有多少个-1，11或00相邻为+1

对于单个ai求出来了，那么从a1~ai的和，就是从i代表的叶子结点，向根结点走一条路线，统计这条路线左边的树的种贡献。

剩下的任务可以交给数位dp了，dp[i][b][j]表示，第i位为根结点，当前二进制位为b（0或1），j表示从当前结点到叶子路径上的01或10相邻的数量，dp值表示此状态下收集到了多少个叶子（因为每个叶子代表一个数字，初始状态dp[0][b][0]=1）

这样可以得到一个完全二叉树下的dp数组。

 

统计时，可以先把n所在的整颗子树统计下来，然后在减掉右边多余的子树。比如询问n=5，则先把0~7这整颗树算进答案，然后在减掉6~7那棵子树的贡献。

这样一次询问的复杂度是log(n)^2，我提交了两遍超时，再试一次竟然AC了，处在超时的边缘。下面可以预处理一个前缀和优化掉一层log

sum[i][j] ：i 结点下，01或10相邻位有j个，sum值为这样的数的个数

del [i][len][pre][j]： i 结点处，i结点所在子树最高的1到叶子的距离为len，i结点以上出现了pre次01或10，i 结点以下出现了j次01或10，del值表示这样的数的个数

然后把这两个数组的最后一维，都处理为前缀和，就可优化掉一层内循环了。

【代码】

#include
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;

ll del[64][64][64][64];
ll sum[64][64]; //本来不需要的，可是总是超时，用来预处理降低复杂度的
ll dp[64][2][64]; //3个参数：dfs层，本层0/1，01边数量
bool vis[64][2];
int bit[64];
int main()
{
    for(int root=0;root<62;root++) //数位dp
    {
        for(int num=0;num<=1;num++)
        {
            if(root==0)
            {
                dp[root][num][0]=1; //叶子结点
            }
            for(int j=0;j<=root;j++) //01边数
            {
                if(num==0)
                {
                    dp[root][num][j]=(dp[root][num][j]+dp[root-1][0][j])%mod;
                    if(j)dp[root][num][j]=(dp[root][num][j]+dp[root-1][1][j-1])%mod;
                }
                else
                {
                    if(j)dp[root][num][j]=(dp[root][num][j]+dp[root-1][0][j-1])%mod;
                    dp[root][num][j]=(dp[root][num][j]+dp[root-1][1][j])%mod;
                }
            }
        }
    }
    for(int i=0;i<62;i++)
    {
        for(int j=0;j<=i;j++)
        {
            sum[i][j]=dp[i][1][j]*abs(i-j*2)%mod;
            if(j) sum[i][j]=(sum[i][j]+sum[i][j-1])%mod; //处理为前缀和
        }
    }
    for(int i=0;i<62;i++) //预处理
    {
        for(int len=0;len<62;len++) //枚举当前位所在的数串的最高位，即长度-1
        {
            for(int pre=0;pre<62;pre++) //枚举当前位所在的数串前面有几次01边
            {
                for(int j=0;j<=i+1;j++) //枚举当前位子树中01边的数量
                {
                    del[i][len][pre][j]=dp[i][1][j]*abs(len-(j+pre)*2)%mod;
                    if(j) del[i][len][pre][j]+=del[i][len][pre][j-1];
                    del[i][len][pre][j]%=mod;
                }
            }
        }
    }
    ll n;int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%lld",&n);
        int top=0;
        while(n){ bit[top++]=n&1;n>>=1; } //分解n二进制
        ll ans=0;
        for(int i=0;i=1;i--) //删去多加的子树
        {
            int len=top-1;
            if(bit[i-1]==0) //右子树1需要删掉
            {
                int pre=bit[i]?side:side+1; //考虑要删除的子树根与父结点是01边则多加一条边
                //ans-=dp[i-1][1][j]*abs(len-(j+pre)*2)%mod;
                ans-=del[i-1][len][pre][i];
                ans=(ans%mod+mod)%mod;
            }
            if(bit[i]^bit[i-1])side++;
        }
        printf("%lld\n",ans);
    }
    return 0;
}