关于BFS的一些拙劣的理解

在写完DFS好久，好久，好久以后，终于想开始写BFS了。。。
主要原因还是因为这段时间一些奇奇怪怪的事太多了，什么网课刷课时啦，老师突然收作业啦，还有啥要实验室考试啦。。。
反正总算是把这些杂事慢慢理顺了，可以开始继续好好学习了，嘿嘿。。。QwQ

1.BFS的用法

BFS的意思是广度(宽度)有些搜索，和DFS一样，它是一种遍历和搜索树或图的算法。不同之处是，DFS的搜素是深度优先的，它的搜素方法是一条路径一条路径的搜查，而 BFS是从起点开始，一行一行的进行搜索的，直至搜索的合法路径。
BFS的实现需要使用到队列，然后通过如下面图示的步骤来进行搜索。

同样的题目改一改：
现在我们从v1出发，走到v10，那么最近的可以到达v10的合法路径是哪条？
现在我们用BFS的思想来对题目进行模拟。
首先，我们先把起始点放进队列，然后开始搜索把他变成绿色。

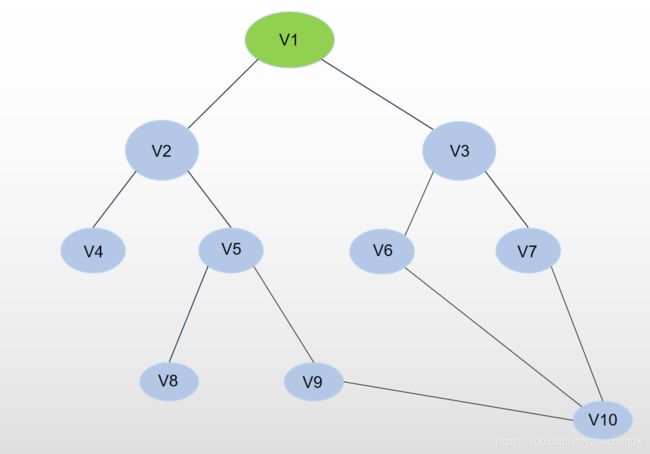
然后发现V1不是答案，于是找到与V1相连接的两个关联点，V2和V3。
这时我们把V2,V3放进队列中，把V1弹出队列，并标记为“以搜查”，把它标记为红色。

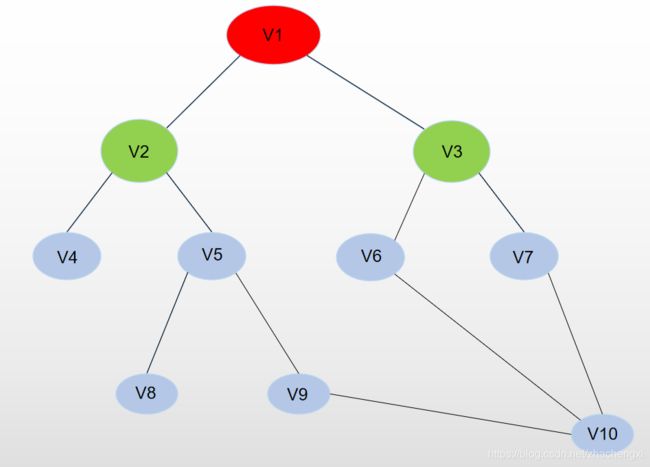
然后继续搜素，发现V2,V3都不到目标点，找到他们的相邻点，V1, V4, V5, V6, V7，因为V1已经被标记搜素过了，所以我们不会再返回V1，我们把V2，V3弹出，并标记为以搜索(红色)，然后，再把V4，V5，V6，V7，压入队列中。

同样的方法，我们再继续深入搜索，把V4，V5，V6，V7弹出，然后把相邻的V8，V9，V10压入，这时，我们就可以搜素到V10，找到最短路径，直接跳出。

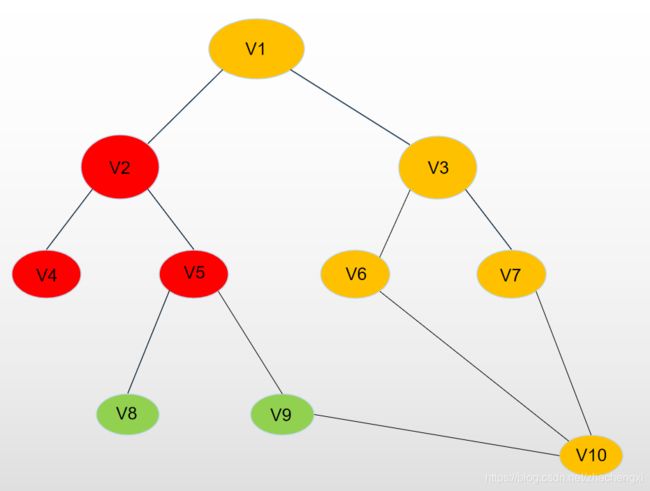
我们可以发现有两条路径的长度是一样的，于是输出两条路径的长度。
BFS在寻找最短路的时候起优势明显大于DFS，它可以在找到目标点后直接跳出，不在继续向下搜索(但是这个题目有点特殊，它在找到最短路径的时候，正好也把所有的点遍历完了。。。是我之前画图的时候没考虑好，也懒得改了)

2.题目例举

实践才能出真知，下面又是愉快的练习时间了~~，一起来看例题吧。

<1>Dungeon Master

这个题目是英文的。。。就不搬题了，可以先点开来看一下题目再看下面的代码

#include
#include
#include
#include
using namespace std;

const int N = 35;
char p[N][N][N];
int vis[N][N][N];    //用来标记是否搜查过
int sx, sy, sz;      //起始点的坐标
int ex, ey, ez;      //输入的值
int go[6][3] = {{0, 0, 1}, {0, 0, -1}, {0, 1, 0}, {0, -1, 0}, {1, 0, 0}, {-1, 0, 0}};  //移动方向。

struct node
{
 	int step, x, y, z;   //定义一个结构体，方便算法实现
};

bool found(int x, int y, int z)     //查询该点是否符合要求
{
 	if(x < 0||y < 0||z < 0||x >= ex||y >= ey||z >= ez)
  		return true;
	 else if(p[x][y][z] == '#')
  		return true;
	 else if(vis[x][y][z])
  		return true;
	 return false;
}

int bfs()
{
	 queue<node> q;    //用node(结构体的类型)定义队列
	 node a, next;  //定义两个数，a为当前量，next为下一个量
	 a.x = sx;     //初始化结构体的值
	 a.y = sy;
	 a.z = sz;
	 a.step = 0;
	 vis[a.x][a.y][a.z] = 1;   //将起始点标记
	 q.push(a);    //压入初始值，开始遍历
	 while(!q.empty())   //当q清空前，不结束
	 {
	 	a = q.front();    //先遍历队列中的第一个值
  		q.pop();   //弹出队列中的第一个值
  		if(p[a.x][a.y][a.z] == 'E')
  			 return a.step;  //如果符合条件，直接返回其值
  		for(int i = 0; i < 6; i ++)
	 	{
	   		next = a;     //对遍历的点进行移动
   			next.x = a.x + go[i][0];
   			next.y = a.y + go[i][1];
   			next.z = a.z + go[i][2];
   			if(found(next.x, next.y, next.z))
    				continue;   //如果不满足条件，则继续搜索
   			vis[next.x][next.y][next.z] = 1;
   			next.step = a.step + 1;
   			q.push(next);
  		}
 	}
 	return 0;
}

int main()
{
 	 while(cin >> ex >> ey >> ez && ex + ey + ez)
  	{
   		for(int i = 0; i < ex; i ++)
		{
    			for(int j = 0; j < ey; j ++)
    			{
     				scanf("%s", p[i][j]);  //这里输入有些小技巧。。。卡了我一段时间
     			for(int q = 0; q < ez; q ++)
     			{
      				if(p[i][j][q] == 'S')
      				{
      					 sx = i, sy = j, sz = q;  //确认起始点的坐标
     				}
     			}
   		 }
   	 }
  	memset(vis, 0, sizeof(vis));
   	int ans;
   	ans = bfs(); 
   	if(ans)
    		cout << "Escaped in " << ans << " minute(s)." << endl;
   	else
    		cout << "Trapped!" << endl;
  	}
  	return 0;
} 

我们就这样愉快的完成了一道BFS的题目，其实和DFS一样，这样的题目主要问题还是关于要怎么把题目转换成一个树或者图，只要在想清楚这点后，这样的题目也就不难解决了，然后我们再看一道题。。。

<2>迷宫问题

迷宫问题是一道非常经典的BFS题目，它的题目要求如下
定义一个二维数组：

int maze[5][5] = {

0, 1, 0, 0, 0,

0, 1, 0, 1, 0,

0, 0, 0, 0, 0,

0, 1, 1, 1, 0,

0, 0, 0, 1, 0,

};

它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。
这个题目也放了超链接，有兴趣可以点开自己做一做，下面是A题代码

#include
#include
#include
#include
#include
#include
#include
#include
#define eps 1e-6
#define PI acos(-1.0)
#define ll long long int
using namespace std;

const int M = 10;

bool a[M][M], vis[M][M];/// a 用来标记是否可走， vis 标记是否走过

struct node
{
    int x, y, time;
};

int Move[4][2] = {{0,-1},{0,1},{-1,0},{1,0}};///上下左右四个方向

void bfs()
{
    map<int, node>PRE[50];///建立起坐标与父节点的联系
    stack<int> st[2];///一个存 y ，一个存 x 并反向输出路径
    struct node p, t;
    queue<node> q;
    p.x = 0;
    p.y = 0;
    p.time = 0;
    q.push(p);
    vis[0][0] = 1;
    while(!q.empty())
        {
            p = q.front();
            q.pop();
            if(p.x == 4 && p.y == 4)/// end up 终点
                break;
            for(int i = 0; i < 4; ++i)
            {
                t = p;
                t.x += Move[i][0];
                t.y += Move[i][1];
                if(a[t.y][t.x] && !vis[t.y][t.x])///若此点可走且没有走过
                {
                    t.time++;
                    PRE[t.y][t.x] = p;///标记 t 的父节点
                    q.push(t);
                    vis[t.y][t.x] = 1;
                    //cout << t.time << endl;
                }
            }
        }
        while(n--)
        {
            st[0].push(p.y);///存入坐标
            st[1].push(p.x);
            p = PRE[p.y][p.x];///返回父节点
        }
        n = st[0].size();
        while(n--)
        {
            cout << '(' << st[0].top() << ", " << st[1].top() << ')' <<'\n';///利用栈的特性进行逆向打印
            st[0].pop();///弹出首元素
            st[1].pop();
        }
}

int main()
{
    memset(vis, 0, sizeof(vis));
    memset(a, 0, sizeof(a));///初始化很重要。。
    int data;
    for(int i = 0; i < 5; ++i)
    {
        for(int j = 0; j < 5; ++j)
        {
            scanf("%d", &data);
            if(data == 0)
                a[i][j] = 1;///若 data 为 0，则说明此点可走，标记该点为 1.
            else
                a[i][j] = 0;
        }
    }
    bfs();
    return 0;
}

感觉这道题目的转换，要比上一道题目的难一点，所以如果能理解这道题目，然后自己独立打出代码了话，应该也就差不多理解BFS的用法了吧。。。QwQ