【2020年杭电暑假第五场】6822 Paperfolding
【2020年杭电暑假第五场】6822 Paperfolding 快速幂+数学推导化简
- 题意
- 思路
- Code(343MS)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=6822
There is a piece of paper in rectangular shape with sufficient length and width (lay flat on the table). Execute an operation instruction according to a string of length n from left to right that only contains 4 different characters of L,R,U,D.
-
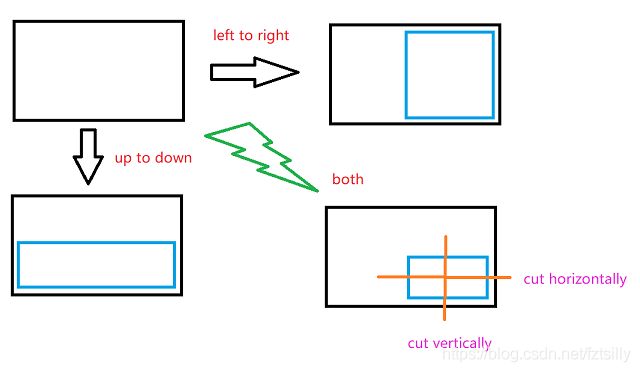
L instruction means to fold it from left to right,
-
R instruction means to fold from right to left,
-
U instruction means to fold from top to bottom,
-
D instruction means to fold in half from bottom to top.
Note that the operation is limited due to the limitation of the desktop. Namely, the fold operation is restricted. For example, if you fold the paper from left to right, you should let the left side overlap on the right side with no rotation.
Now, cut a knife horizontally (completely cut) at the center of the visible part of the paper, and then cut vertically (completely cut).
The number of pieces of the whole paper split is num(S).
See the example and the picture for better understanding.
Now given a nonnegative integer n, the string S is generated from 4n different possible outcomes in equal probability. Find the expected value of the number of pieces of the paper which is split, that is E(num(S)) mod 998244353.
It can be shown that the answers can be represented by PQ, where P and Q are coprime integers, and print the value of P×Q−1 mod 998244353.
Input
The first line contains a single integer T (1≤T≤105), the number of testcases.
Each of the next T lines contains a number n ( 0≤n≤1018 ).
Output
For each testcase, print the answer in one line.
Sample Input
2
0
1
Sample Output
4
6
Source
2020 Multi-University Training Contest 5
题意
在一块无限大的纸上,有四种操作,上折,下折,左折,右折,问k次操作后,折完后取中点,横竖分别切一刀(切十字),问最后纸分成多少片的数学期望(又是数学期望,哎)。
思路
左右折是一样的,上下折是一样的,所以只有两种操作。
应该实验(手动剪纸)可得,往上下方向折 k k k次,会有 2 k 2^k 2k条割线,那么横着切一刀展开后的纸片数有 2 k + 1 2^k+1 2k+1张,这个 + 1 +1 +1就是最中间折痕左右两边纸片算一个,同理左右折。
在折 n n n次的情况下,设左右折次数为 k k k,那么上下折次数为 n − k n-k n−k。
根据上面描述,左右折 k k k次,则横着切一刀后有纸片数为 2 k + 1 2^k+1 2k+1,则竖着切一刀后有纸片数为 2 n − k + 1 2^{n-k}+1 2n−k+1,则横竖切一刀后总纸片数为 ( 2 k + 1 ) ∗ ( 2 n − k + 1 ) (2^k+1)*(2^{n-k}+1) (2k+1)∗(2n−k+1)。
这 k k k中是在 n n n种操作中选出来的 k k k种,所以结果还要乘上 C n k C_n^k Cnk。
因为求的是数学期望,每种操作可以选左右折或者上下折,所以结果要乘 1 2 n \frac{1}{2^n} 2n1。
最后答案为 ∑ k = 0 n ( 2 k + 1 ) ∗ ( 2 n − k + 1 ) C n k 2 n \frac{\sum_{k=0}^{n}(2^k+1)*(2^{n-k}+1)C_n^k}{2^n} 2n∑k=0n(2k+1)∗(2n−k+1)Cnk
一步一步化简:
∑ k = 0 n ( 2 n + 2 n − k + 2 k + 1 ) C n k 2 n \frac{\sum_{k=0}^{n}(2^n+2^{n-k}+2^k+1)C_n^k}{2^n} 2n∑k=0n(2n+2n−k+2k+1)Cnk
由二项式定理可得 C n k = ( 1 + 1 ) n C_n^k=(1+1)^n Cnk=(1+1)n,继续化简:
2 n + 1 + ∑ k = 0 n ( 2 n − k + 2 k ) C n k 2 n 2^n + 1+\frac{\sum_{k=0}^{n}(2^{n-k}+2^k)C_n^k}{2^n} 2n+1+2n∑k=0n(2n−k+2k)Cnk
2 n + 1 + ∑ k = 0 n ( 2 n − k C n k + 2 k C n k ) 2 n 2^n + 1+\frac{\sum_{k=0}^{n}(2^{n-k}C_n^k+2^kC_n^k)}{2^n} 2n+1+2n∑k=0n(2n−kCnk+2kCnk)
由 C n k = C n n − k C_n^k=C_n^{n-k} Cnk=Cnn−k继续化简:
2 n + 1 + ∑ k = 0 n ( 2 n − k C n n − k + 2 k C n k ) 2 n 2^n + 1+\frac{\sum_{k=0}^{n}(2^{n-k}C_n^{n-k}+2^kC_n^k)}{2^n} 2n+1+2n∑k=0n(2n−kCnn−k+2kCnk)
2 n + 1 + 2 ∗ ∑ k = 0 n ( 2 k C n k ) 2 n 2^n + 1+\frac{2*\sum_{k=0}^{n}(2^kC_n^k)}{2^n} 2n+1+2n2∗∑k=0n(2kCnk)
由二项式定理可得 ∑ k = 0 n 2 k C n k = ( 2 + 1 ) n \sum_{k=0}^{n}2^kC_n^k=(2+1)^n ∑k=0n2kCnk=(2+1)n继续化简:
2 n + 1 + 2 ∗ 3 n 2 n 2^n + 1+\frac{2*3^n}{2^n} 2n+1+2n2∗3n
所以这一题可以用快速幂加逆元求解。
Code(343MS)
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ll;
typedef long double ld;
typedef pair<int, int> pdd;
#define INF 0x7f7f7f
#define mem(a,b) memset(a , b , sizeof(a))
#define FOR(i, x, n) for(int i = x;i <= n; i++)
const ll mod = 998244353;
// const int maxn = 1e5;
// const double eps = 1e-6;
const ll inv2 = 499122177;
ll quick_pow(ll a, ll b)
{
ll ans = 1, base = a;
while(b != 0)
{
if(b&1)
{
ans = ans * base;
ans %= mod;
}
base = base * base % mod;
b >>= 1;
}
return ans;
}
void solve()
{
int T;
cin >> T;
while(T--)
{
ll N;
cin >> N;
if(N == 0)
{
cout << 4 << endl;
continue;
}
ll k = (2 * quick_pow(3 * inv2 % mod, N) % mod + quick_pow(2, N) + 1) % mod;
cout << k << endl;
}
}
signed main()
{
solve();
return 0;
}
比赛的时候化简的过程中出现的问题,还是我太菜了,呜呜呜。