龙良曲pytorch基础课程学习笔记

什么是Pytorch?

PyTorch 是一个基于 Python 的科学计算包，主要定位两类人群：

• NumPy 的替代品，可以利用 GPU 的性能进行计算
• 深度学习研究平台拥有足够的灵活性和速度

初步了解

tensor对象

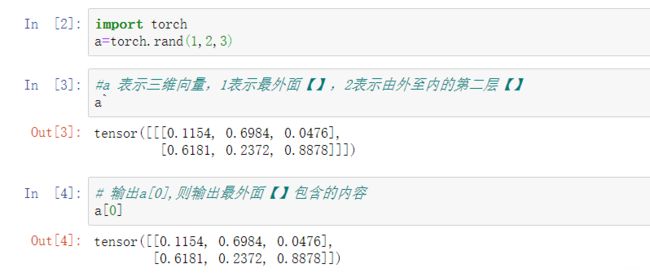
在 TensorFlow 中，数据不是以整数，浮点数或者字符串形式存在的，而是被封装在一个叫做 tensor 的对象中。Tensor是张量的意思，张量包含了0到任意维度的量，其中，0维的叫做常数，1维的叫做向量，二维叫做矩阵，多维度的就直接叫张量。

举例：print(x[: ，1]) 输出结果如下：

tensor([ 0.4477, -0.0048,  1.0878, -0.2174,  1.3609])

常用方法

item()：如果有一个元素 tensor ，可使用 .item() 来获得这个 value

x = torch.randn(1)
print(x)
print(x.item())

tensor([ 0.9422])
0.9422121644020081

**view()：**view()函数作用是将一个多行的Tensor拼接成一行
举例：

import torch
a = torch.Tensor(2,3)
print(a)
# tensor([[0.0000, 0.0000, 0.0000],
#    [0.0000, 0.0000, 0.0000]])
 
print(a.view(1,-1))
tensor([[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]））      

pytorch神经网络

相关函数说明

神经网络可以通过 torch.nn 包来构建。
神经网络是基于自动梯度 (autograd)来定义一些模型。一个 nn.Module 包括层和一个方法 forward(input) 它会返回输出(output)。

主要方法解释
nn.conv2d()：对由多个输入平面组成的输入信号进行二维卷积
参数理解：
in_channels:
1）输入通道数，对于图片层一般为1（灰度）3（RGB）
2）定义一种输入规则，要求上一层的输出必须和这个输入一致，也可以理解为并发in_channels个channel在上一层
out_channels:
1)直观理解是输出层通道数，
2)换一种理解是kernels（卷积核）/filter个数，其中，每个卷积核会输出局部特征

layer = nn.Conv2d(in_channels=1,out_channels=3,kernel_size=3,stride=1,padding=0)

具体可以参考博文：链接入口

人工神经网络举例

定义了Net类，过程：conv1->max_pool->conv2->fc1->reLU()->fc2->reLU()->fc3

import torch
import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 5x5 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features

net = Net()
print(net)

输出结果：

Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

学习笔记

pytorch基础

维度dim=3：

维度dim=4

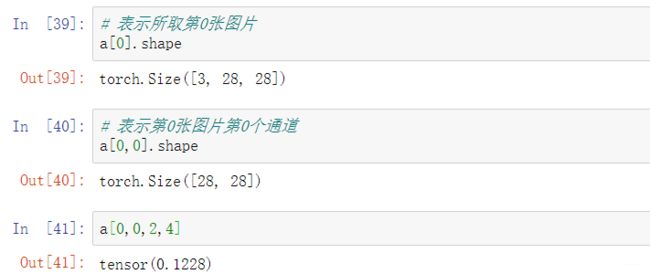
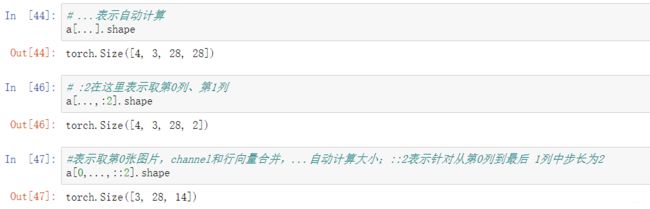
*# 最外层【】包括两个【【【....】】】,
#针对其中一个【【【....】】】，它的下一层里面包括3个【【】】,
#再往里面一层（即倒数第二层）则包括着28*28维度，
#最后一层则是1*28大小* 

tensor([[[[0.1423, 0.1688, 0.3506,  ..., 0.2932, 0.8334, 0.8482],
          [0.3695, 0.5737, 0.0264,  ..., 0.9051, 0.6323, 0.7968],
          [0.0968, 0.7193, 0.5856,  ..., 0.7815, 0.8179, 0.9050],
          ...,
          [0.4456, 0.6376, 0.8379,  ..., 0.2708, 0.8039, 0.8024],
          [0.2216, 0.1665, 0.0808,  ..., 0.0633, 0.4367, 0.1745],
          [0.1007, 0.1041, 0.9349,  ..., 0.5848, 0.2087, 0.1483]],

         [[0.0829, 0.6656, 0.9761,  ..., 0.4090, 0.1196, 0.5291],
          [0.4716, 0.5912, 0.7128,  ..., 0.1953, 0.2334, 0.9411],
          [0.2104, 0.1102, 0.6728,  ..., 0.8068, 0.9950, 0.4371],
          ...,
          [0.7302, 0.6368, 0.1293,  ..., 0.9385, 0.4720, 0.7418],
          [0.7596, 0.6282, 0.3802,  ..., 0.3436, 0.1603, 0.2718],
          [0.5329, 0.0867, 0.6653,  ..., 0.3291, 0.9281, 0.9751]],

         [[0.3201, 0.1916, 0.2129,  ..., 0.2332, 0.8030, 0.1057],
          [0.9940, 0.7888, 0.3779,  ..., 0.8681, 0.0063, 0.7336],
          [0.7583, 0.5838, 0.9530,  ..., 0.5899, 0.3200, 0.5285],
          ...,
          [0.7574, 0.9169, 0.0390,  ..., 0.0037, 0.0503, 0.3663],
          [0.3218, 0.8958, 0.1545,  ..., 0.0294, 0.4383, 0.7682],
          [0.9043, 0.8152, 0.2490,  ..., 0.4415, 0.0417, 0.5950]]],


        [[[0.4197, 0.8741, 0.8705,  ..., 0.0110, 0.9247, 0.7600],
          [0.9980, 0.2174, 0.4711,  ..., 0.4653, 0.9348, 0.2743],
          [0.4612, 0.8228, 0.4504,  ..., 0.0373, 0.9810, 0.3891],
          ...,
          [0.9348, 0.3263, 0.3506,  ..., 0.4719, 0.5430, 0.4312],
          [0.5439, 0.3929, 0.1338,  ..., 0.6726, 0.3350, 0.2187],
          [0.0106, 0.2521, 0.5947,  ..., 0.2532, 0.5134, 0.1940]],

         [[0.5895, 0.7871, 0.6963,  ..., 0.3664, 0.1130, 0.3922],
          [0.9905, 0.0790, 0.6351,  ..., 0.9541, 0.0691, 0.4853],
          [0.8415, 0.8071, 0.1111,  ..., 0.8163, 0.7393, 0.0135],
          ...,
          [0.8231, 0.9084, 0.9422,  ..., 0.0301, 0.2185, 0.5539],
          [0.6521, 0.9678, 0.4565,  ..., 0.8952, 0.7013, 0.6616],
          [0.1426, 0.0082, 0.0164,  ..., 0.2047, 0.7086, 0.8364]],

         [[0.8879, 0.9367, 0.6665,  ..., 0.4427, 0.6667, 0.3754],
          [0.1574, 0.2330, 0.5255,  ..., 0.1370, 0.2358, 0.7717],
          [0.5735, 0.0059, 0.5689,  ..., 0.9262, 0.7181, 0.1654],
          ...,
          [0.6867, 0.6018, 0.1975,  ..., 0.2262, 0.6240, 0.1855],
          [0.0466, 0.6741, 0.3328,  ..., 0.0284, 0.0890, 0.9005],
          [0.6681, 0.9575, 0.2159,  ..., 0.2985, 0.0439, 0.5840]]]])

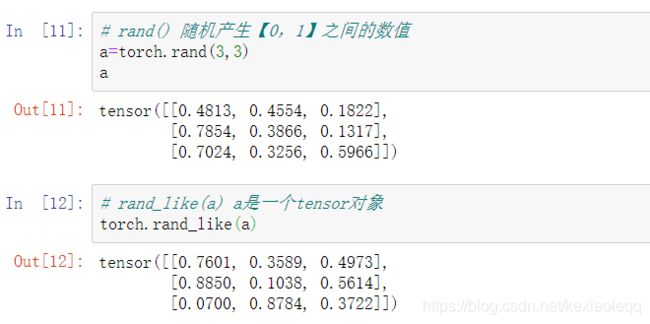
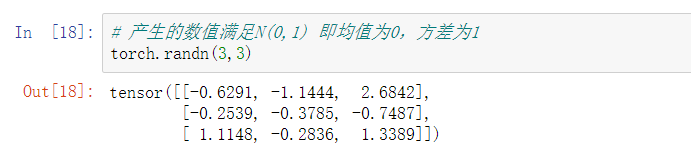
创建tensor

1. import form numpy

2. rand/rand_like,randint

3. randn、normal

4. full

4. arange/range

5. linspace/logspace

6.zeros/ones/eye

7.randperm

8. indexing

9. :: / …

10.masked_select

将Tensor多维对象转化为一维（打平），筛选出符合要求的值

Tensor转换

1. View/reshape

2. Squeeze/unsqueeze

（1）Squeeze
只能挤压掉维度为1的
特别注意：从前往后插入，插入位置为索引前面
从后往前插入时，插入位置为索引后面

举例：如下图
（2) unsqueeze

3. expand

4. repeat

5. t/transpose

维度交换操作
**1 .t() ** 只针对二维的矩阵进行行列操作(转置操作)

2. transpose()

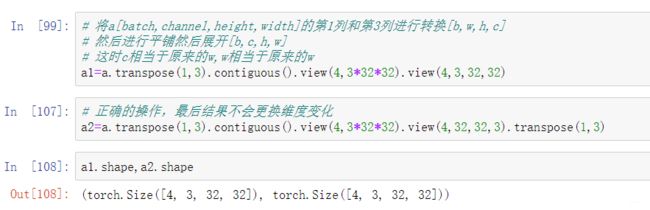
6. permute

permute的参数是索引的下标值

Pytorch进阶

1. Broadcasting

match from last dim
自动扩展

2. 拼接与拆分

（1）Cat

dim=0 表示第0维进行合并（对于二维来说，也就是行增加）
dim=1表示第1维进行合并（对于二维来说，也就是列增加）
前提：其余维度的数量相同

（2）Stack

与Cat的根本区别：

1. Cat不需要添加新维度，是在原来的维度上进行拼接，进行拼接的维度不一样，其余维度必须一样；
2. Stack会创建新维度，其余维度也需要保持一样

（3）Split

拆分
1. 数量拆分
3. 长度拆分

3. 数学运算

（1) matmul / @

mm()也表示矩阵乘运算，mm只针对二维矩阵
表示矩阵的乘法运算

多维度进行乘法运算，是基于最后面的两维数据进行操作的

（2) Approxiimate

floor：向下取整
ceil：向上取整
trunc() ：取整数部分
frac()：取小数部分
round()：四舍五入

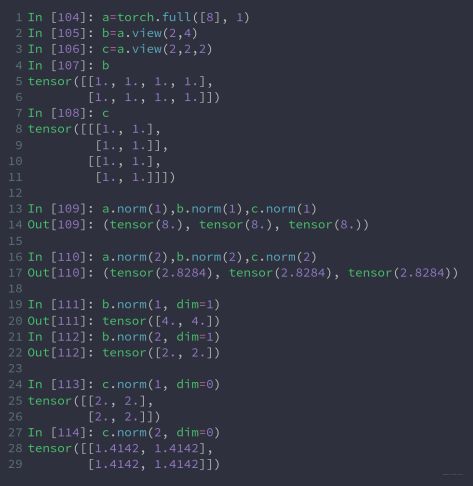
（3) norm

范数操作
范数公式如下：

注意：维度dim取值为0则合并多行
维度dim=1则合并多列
举例：

（4) min/mean/prod

prod：表示累乘

（5) argmin/argmax

argmax和argmin返回最大值的索引值
会将多维数据打平，然后重新计算索引值

（6) topk

topk ：用来求tensor中某个dim的前k大或者前k小的值以及对应的index

torch.topk(input, k, dim=None, largest=True, sorted=True, out=None) ->
(Tensor, LongTensor)

• input：一个tensor数据
• k：指明是得到前k个数据以及其index
• dim： 指定在哪个维度上排序， 默认是最后一个维度
• largest：如果为True，按照大到小排序； 如果为False，按照小到大排序
• sorted：返回的结果按照顺序返回
• out：可缺省，不要

import torch

pred = torch.randn((4, 5))
print(pred)
values, indices = pred.topk(1, dim=1, largest=True, sorted=True)
print(indices)
# 用max得到的结果，设置keepdim为True，避免降维。因为topk函数返回的index不降维，shape和输入一致。
_, indices_max = pred.max(dim=1, keepdim=True)

print(indices_max == indices)
# pred
tensor([[-0.1480, -0.9819, -0.3364,  0.7912, -0.3263],
        [-0.8013, -0.9083,  0.7973,  0.1458, -0.9156],
        [-0.2334, -0.0142, -0.5493,  0.0673,  0.8185],
        [-0.4075, -0.1097,  0.8193, -0.2352, -0.9273]])
# indices, shape为 【4,1】,
tensor([[3],   #【0,0】代表 第一个样本最可能属于第一类别
        [2],   # 【1, 0】代表第二个样本最可能属于第二类别
        [4],
        [2]])
# indices_max等于indices
tensor([[True],
        [True],
        [True],
        [True]])

（7) 高阶操作

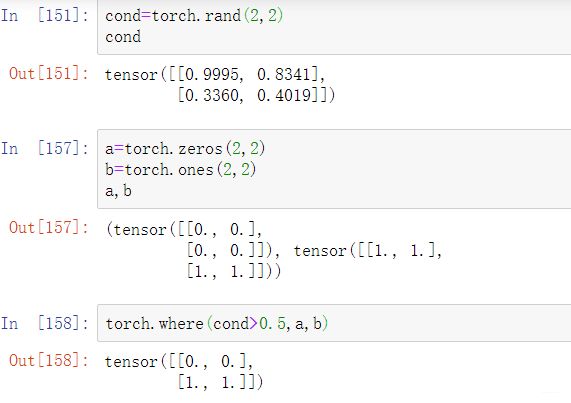
where

gather

torch.gather(input, dim, index, out=None) → Tensor

首先，我们要看dim=1 or 0，这分别对应不同的维度进行操作，本例中dim=1表示在横向，所以索引就是列号。

>>> t = torch.Tensor([[1,2],[3,4]])
>>> torch.gather(t,1,torch.LongTensor([[0,0],[1,0]])
1  1
4  3
[torch.FloatTensor of size 2x2]

index的第一行为[0,0]，第一个0索引到第一列即为1，第二个0也索引到第一列即为1；index的第二行为[1,0]，其中1索引到第二列即为4,0索引到第一列即为3。

4. 交叉熵

交叉熵：指预测值和真实概率之间的距离，交叉熵是一个信息论中的概念，它原来是用来估算平均编码长度的。给定两个概率分布p和q，通过q来表示p的交叉熵为：

交叉熵刻画的是两个概率分布之间的距离，或可以说它刻画的是通过概率分布q来表达概率分布p的困难程度，p代表正确答案，q代表的是预测值，交叉熵越小，两个概率的分布约接近

在神经网络中怎样把前向传播得到的结果也变成概率分布呢？
Softmax回归就是一个非常有用的方法， 假设原始的神经网络的输出为，那么经过Softmax回归处理之后的输出为：

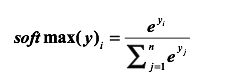
举例：假设有一个3分类问题，某个样例的正确答案是（1，0，0），这个模型经过softmax回归之后的预测答案是（0.5，0.4，0.1），那么预测和正确答案之间的交叉熵为：

举个例子，假设有一个3分类问题，某个样例的正确答案是（1，0，0），这个模型经过softmax回归之后的预测答案是（0.5，0.4，0.1），那么预测和正确答案之间的交叉熵为：

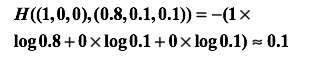
显然我们看到第二个预测要优于第一个。这里的（1，0，0）就是正确答案p，（0.5，0.4，0.1）和（0.8，0.1，0.1）就是预测值q，显然用（0.8，0.1，0.1）表达（1，0，0）的困难程度更小，也就是p,q两值相近程度。
详见：参考博文入口

5. 动量（momentum）与学习衰减

momentum：称之为动量或者惯性
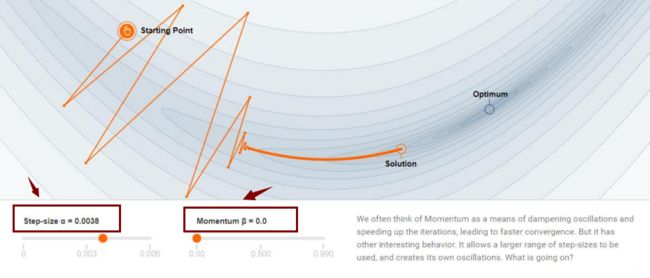
当momentum取值为0的时候，如下图所示。
梯度下降方向沿着方框中变化量的方向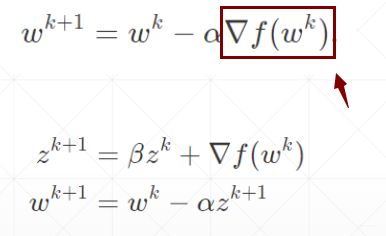
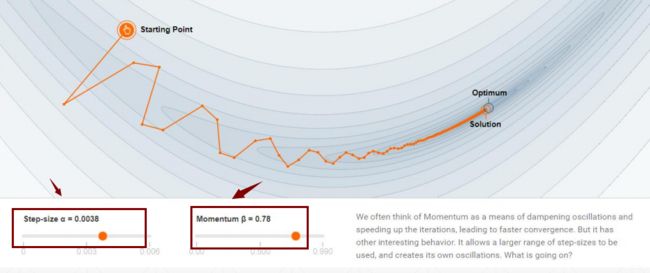
当momentum取值不为0的时候，如果取值到达局部最小值时，由于惯性的存在，可以冲出去找到最广阔的天空，从而找到全局最优。

6. dropout

dropout:就是减少连接数
pytorch中的参数是dropout_prob

pytorch中的参数是keep_prob

7. 卷积神经网络

常用卷积核（Convolution Kernel）

卷积运算公式

池化与采样

subsampling：向下采样
池化：最大池化、平均池化
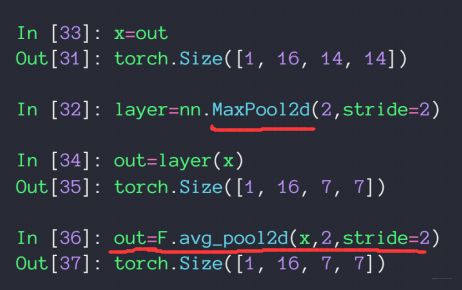
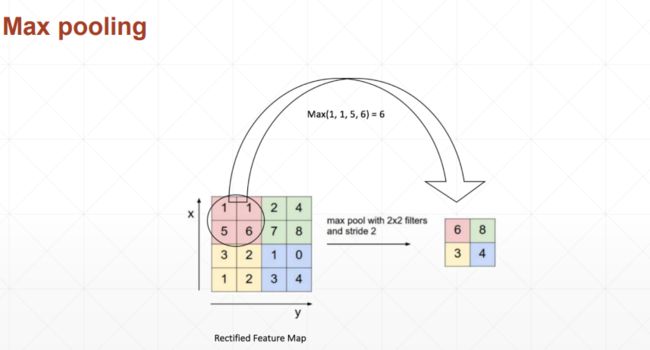对应的函数为：nn.MaxPool2d()、F.avg_pool2d() # 分别表示2维空间内求最大池化以及平均池化

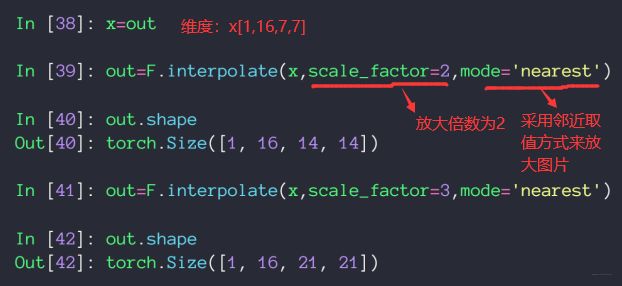
upsampling：向上采样
通过对原有像素进行操作从而将图片放大
函数：F.interpolate()

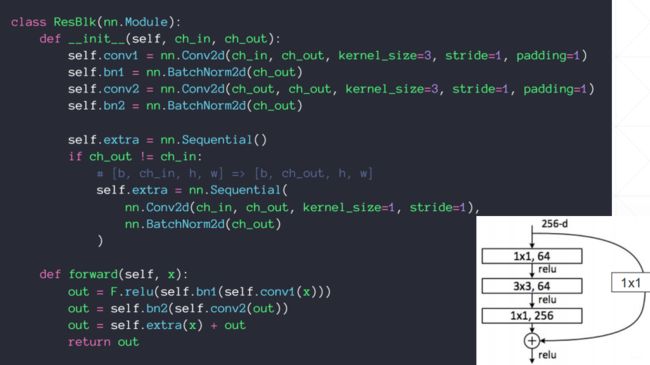
经典卷积神经网络

代码实现：

nn.moudle

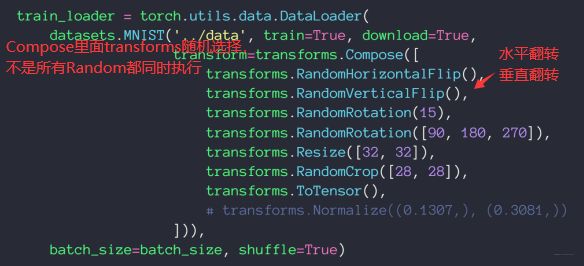
数据增强

(1) Flip

翻转（水平和垂直）

(2) Rotate

旋转（角度）

(3) Scale

缩放

(4) Crop Part

裁剪

(5) Noise

噪声处理
操作主要代码如下