数据结构:链表、队列、二叉树 python代码实现
顺序表
顺序表两种存储模式*(顺序和元素外置):
- 顺序存储模式:适用于列表中存储的都是同一种元素。
- 元素外置存储模式:适用于列表中存储不同的元素,先开辟空间存储每一个数据,用顺序表存储列表中每一个元素的地址。
顺序表两种存储结构:(一体式和分离式)
- 区别在于,当存储的元素超过了顺序表的存储容量时,分离式存储结构的标头不需要再次申请地址,只需要改变标头中第三次元素(存储元素的第一个地址,即200所在的地址0x23)
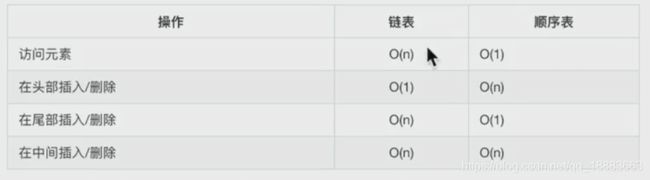
顺序表和链表的区别
单链表代码实现
class Node(object):
def __init__(self,elem):
self.elem = elem
self.next = None
class Single_link(object):
def __init__(self,node = None):
self.__head = node
def is_empty(self):
return self.__head == None #布尔类型
def length(self):
cur = self.__head # cur.next 表示的是一个存在的节点, 如果不存在就会报错
count = 0
while cur!= None:
cur = cur.next
count += 1
return count
def travel(self):
"""遍历"""
cur = self.__head
while cur !=None:
print(cur.elem,end=' ')
cur = cur.next
print(' ')
def append(self,item):
"""链表尾部添加元素"""
node = Node(item)
if self.is_empty():
self.__head = node
else:
cur = self.__head
while cur.next != None:
cur = cur.next
cur.next = node
def add(self, item):
"""链表头部添加元素"""
node = Node(item)
node.next =self.__head
self.__head = node
def insert(self, pos, item):
"""链表指定位置添加元素"""
if pos <= 0:
self.add(item)
elif pos > self.length():
self.append(item)
else:
count = 0
pro_cur = self.__head
while count < pos-1:
pro_cur = pro_cur.next
count += 1
node = Node(item)
node.next = pro_cur.next
pro_cur.next = node
def remove(self, item):
'''删除某个数字'''
cur = self.__head
pre = None
while cur != None:
if cur.elem == item:
if cur == self.__head:
self.__head = cur.next
else:
pre.next = cur.next
break
else: # 不是这个数字,继续往下走
pre = cur
cur = cur.next
def rearch(self, item):
cur = self.__head
while cur != None:
if cur.elem == item:
return True
else:
cur = cur.next
return None
if __name__ == '__main__':
ll = Single_link()
双链表代码实现
class Node(object):
def __init__(self,elem):
self.elem = elem
self.next = None
self.prev = None
class Double_link(object):
def __init__(self,node = None):
self.__head = node
def is_empty(self):
return self.__head == None #布尔类型
def length(self):
cur = self.__head
count = 1
while cur != None:
count += 1
cur = cur.next
return count
def travel(self):
cur = self.__head
while cur != None:
print(cur.elem, end=" ")
cur = cur.next
print('')
def append(self,item):
"""链表尾部添加元素"""
node = Node(item)
if self.is_empty():
self.__head = node
else:
cur = self.__head
while cur.next != None:
cur =cur.next
cur.next = node
node.prev = cur
def add(self, item):
"""链表头部添加元素"""
node = Node(item)
node.next = self.__head
self.__head = node
def insert(self, pos, item):
"""链表指定位置添加元素"""
if pos <= 0:
self.add(item)
elif pos > self.length():
self.append(item)
else:
cur = self.__head
count = 0
node = Node(item)
while cur != None:
if count == pos:
node.prev = cur.prev
cur.prev.next = node
node.next = cur
cur.prev = node
break
else:
count += 1
cur = cur.next
def remove(self, item):
'''删除某个数字'''
cur = self.__head
while cur != None:
if cur.elem == item:
# 当删除的为头结点
if cur == self.__head:
self.__head = cur.next
# 当头结点不唯一时
if cur.next:
cur.next.prve = None
else:
# 当该结点不是尾部结点
cur.prev.next = cur.next
if cur.next:
cur.next.prve = cur.prev
break
else:
cur = cur.next
def rearch(self, item):
cur = self.__head
while cur != None:
if cur.elem == item:
return True
else:
cur = cur.next
return None
if __name__ == '__main__':
ll = Double_link()
栈代码实现
class stack(object):
def __init__(self):
self.__list = []
def push(self, item):
"""添加一个新的元素到栈顶"""
self.__list.append(item)
def pop(self):
"""弹出栈顶元素"""
return self.__list.pop()
def peek(self):
if self.__list:
return self.__list[-1]
"""返回栈顶元素"""
def is_empty(self):
"""判空"""
return self.__list == []
def size(self):
"""返回栈的元素个数"""
return len(self.__list)
if __name__ == '__main__':
s = stack()
s.push(1)
s.push(2)
s.push(3)
print(s.size())
print(s.peek())
print(s.pop())
print(s.pop())
print(s.pop())
print(s.peek())
print(s.size())
队列代码实现
class Quene(object):
"""队列 尾部添加 头部删除"""
def __init__(self):
self.__list = []
def insert_queue(self, item):
"""向队列中添加一个元素"""
self.__list.append(item)
def del_queue(self):
"""从队列头部删除一个函数"""
return self.__list.pop(0)
def is_empty(self):
"""判空"""
return self.__list == []
def size(self):
"""返回队列大小"""
return len(self.__list)
if __name__ == '__main__':
s = Quene()
print(s.is_empty())
s.insert_queue(1)
print(s.is_empty())
s.insert_queue(2)
s.insert_queue(3)
print(s.size())
print(s.del_queue())
print(s.del_queue())
print(s.del_queue())
print(s.size())
print(s.is_empty())
二分查找代码实现
def binary_search_1(alist, item):
"""递归法实现二分查找"""
n = len(alist)
# 设置退出条件
if n > 0:
mid = n//2
if alist[mid] == item:
return True
elif alist[mid] > item:
return binary_search_1(alist[:mid], item)
else:
return binary_search_1(alist[mid+1:], item)
return False
def binary_search_2(alist, item):
"""二分查找 非递归实现"""
n = len(alist)
start = 0
end = n-1
while start <= end:
mid = (start + end) // 2
if alist[mid] == item:
return True
elif alist[mid] > item:
end = mid-1
else:
start = mid+1
return False
if __name__ == '__main__':
list = [1,2,3,4,5,6]
print(binary_search_1(list, 6))
print(binary_search_1(list, 1))
print(binary_search_2(list, 6))
print(binary_search_2(list, 1))
树的概念与二叉树代码实现
-
常见树结构:满二叉树:满子树
完全二叉树:最后一层可以不满,但是要靠左,子树为0,1都行
平衡二叉树:最后一层只要有子树,就必须是两个
二叉排序树:结点值为 左<中<右
哈夫曼树、B树。 -
二叉树特征:
性质1:第i层最多有2^(i-1)个结点
性质2:深度为K的二叉树最多有2^(k-1)个结点
性质3:叶结点数为X,度为2的结点总是为Y,X = Y+1。
性质4:n个结点的完全二叉树,深度为log2(n+1)
性质5:完全二叉树,从上到下,从左到右的编码,编号为i的结点,其左孩子必为2i,右孩子为2i+1;双亲为i/2(i=1时为根,除外) -
广度优先遍历:层次遍历 (使用队列来添加)
-
深度优先遍历:
前序遍历:根 左 右 (先根遍历)
中序遍历:左 根 右 (中根遍历)
后序遍历:左 右 根 (后根遍历)
代码实现
class Node(object):
def __init__(self, item):
self.item = item
self.lchild = None
self.rchild = None
class Tree(object):
'''二叉树'''
def __init__(self):
self.root = None
def add(self, item):
node = Node(item)
queue = [self.root]
if self.root == None:
self.root = node
return
# 通过队列来实现 [A B C D E ] 从左边取判断是否为空 ,空就直接添加,不空的话添加到队列右侧
while queue:# [None]的值为True
cur_node = queue.pop(0)
if cur_node.lchild is None:
cur_node.lchild = node
return
else:
queue.append(cur_node.lchild)
if cur_node.rchild is None:
cur_node.rchild = node
return
else:
queue.append(cur_node.rchild)
def breadth_travel(self):
'''广度遍历'''
queue = [self.root]
if self.root == None:
return
while queue:
cur_node = queue.pop(0)
print(cur_node.item, end=' ')
if cur_node.lchild:
queue.append(cur_node.lchild)
if cur_node.rchild:
queue.append(cur_node.rchild)
print(' ')
def preorder(self, node):
"""前序遍历"""
if node is None:
return
print(node.item, end=' ')
self.preorder(node.lchild)
self.preorder(node.rchild)
def midorder(self, node):
"""中序遍历"""
if node is None:
return
self.midorder(node.lchild)
print(node.item, end=' ')
self.midorder(node.rchild)
def postorder(self, node):
"""后序遍历"""
if node is None:
return
self.postorder(node.lchild)
self.postorder(node.rchild)
print(node.item, end=' ')
if __name__ == '__main__':
tree = Tree()
for i in range(10):
tree.add(i)
tree.breadth_travel()
tree.preorder(tree.root)
print(' ')
tree.midorder(tree.root)
print(' ')
tree.postorder(tree.root)