2020 Multi-University Training Contest 2(1001 并查集 1006 hash 1010 爆搜 1012 序列自动机+最长公共子序列)
比赛链接
1001-Total Eclipse
题意:n个点,m条边的 图,每次选择k个联通的点,所有的点的权值减1,问最少执行多少次操作使得 所有点的权值为0
做法:枚举权值从大到小的点,然后遍历周围的点,如果周围的点 之前出现过且能够到达,那么就 把周围的点减去 当前权值,就实现了选多个点一起减,这样下去 操作数是最少的,接着把两个点连成一个联通块。
#include
using namespace std;
#define ll long long
ll input(){
ll x=0,f=0;char ch=getchar();
while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
return f? -x:x;
}
#define PII pair
#define fr first
#define sc second
#define mp make_pair
const int N=1e5+7;
int n,m;
ll Ans=0;
vector G[N];
PII a[N];
ll vis[N],ans[N];
int fa[N],rk[N],vs[N];
int find(int x){ return fa[x]==x? x:(fa[x]=find(fa[x]));}
void merge(int x,int y){
x=find(x);y=find(y);
x==y? 0:rk[x]>=rk[y]? fa[y]=x,rk[x]+=rk[y]:fa[x]=y,rk[y]+=rk[x];
}
int main(){
int T=input();
while(T--){
n=input(),m=input();
int sta=1;Ans=0;
for(int i=1;i<=n;i++){
int val=input();
a[i]=mp(val,i);
fa[i]=i,rk[i]=1,G[i].clear();
vis[i]=0,ans[i]=0;vs[i]=0;
}
for(int i=1;i<=m;i++){
int u=input(),v=input();
G[u].push_back(v),G[v].push_back(u);
}
sort(a+1,a+1+n);
for(int i=n;i>=1;i--){
int u=a[i].sc,val=a[i].fr;
int cnt=0;
// cout<
1006-The Oculus
题意:给定a数组 只包含0和1 第i位为1 代表第i个斐波那契数贡献 权值,把所有贡献的权值和加起来就是A的值
类似的b数组 得到B。将A*B等于值 用c数组表示。
c数组已经给你,但是某一位的1 被改成0 了,问被改的那一位是哪一位
做法:hash做法,将斐波那契数hash,A hash得到,B hash得到,然后枚举c数组得到hash值 C 判断是否等于A*B的hash值即可
#include
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define per(i,a,b) for(int i=a;i>=(b);--i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb emplace_back
#define pii pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
inline ll read()
{
ll x=0,w=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();}
return w==1?x:-x;
}
const int N=2e6+10;
typedef long long ll;
const ll mod=998244353;
ll a[N],b[N],c[N],dp[N];
int n,m,k;
void solve()
{
ll A=0,B=0,C=0;
rep(i,1,n) if(a[i]) A=(A+dp[i])%mod;
rep(i,1,m) if(b[i]) B=(B+dp[i])%mod;
rep(i,1,k) if(c[i]) C=(C+dp[i])%mod;
ll tar=A*B%mod;
//printf("tar:%lld\n",tar);
rep(i,1,k)
{
if(c[i]) continue;
if((C+dp[i])%mod==tar){
printf("%d\n",i);return ;
}
}
puts("1");
}
int main()
{
dp[1]=1,dp[2]=2;
for(int i=3;i 1010-Lead of Wisdom
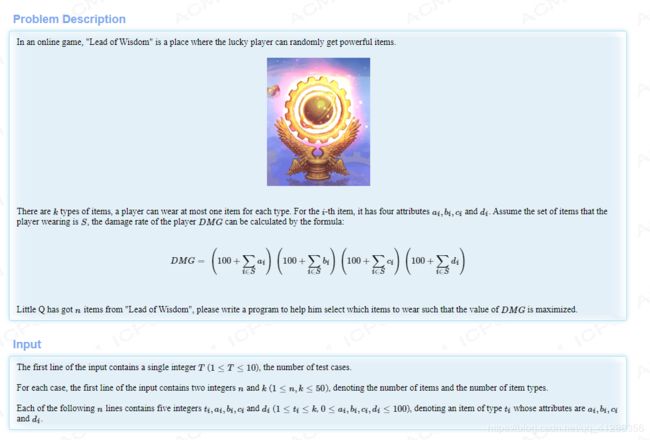
题意:给你 k种 数值 包含 ty[i] a[i] b[i] c[i] d[i] ,每种只能选一个,问如何选使得上图的公式值最大化
做法:官方做法:爆搜
我赛时 水过的方法,分组背包,但是被hack了。
四个变量 ,开思维5000的数组肯定会爆,于是我就尝试了下 把所有的数变成一维,没想到直接一发AC了。
hack数据:
10 3 2 1 10 10 10 10 1 20 0 0 20 2 0 20 20 0
#include
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define per(i,a,b) for(int i=a;i>=(b);--i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb emplace_back
#define pii pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
inline ll read()
{
ll x=0,w=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();}
return w==1?x:-x;
}
const int N=50;
int n,m,k;
struct node
{
ll s;
ll a,b,c,d;
void up()
{
s=0,a=0,b=0,d=0;
}
}dp[55][20010];
vectorG[N];
ll run(ll p1,ll p2,ll p3,ll p4,ll a,ll b,ll c,ll d)
{
//cout<=400;--p) dp[i][p]=dp[i-1][p];
for(int p=sum;p>=400;--p){
for(int j=0;j=400){
//if(p-nx==400) printf("p-nx:%d s:%lld\n",p-nx,dp[i-1][400]);
ll tmp=run(dp[i-1][p-nx].a,dp[i-1][p-nx].b,
dp[i-1][p-nx].c,dp[i-1][p-nx].d,
G[i][j].a,G[i][j].b,G[i][j].c,G[i][j].d);
// cout<dp[i][p].s){
// dp[i][p].s=dp[i-1][p-nx].s+tmp;
// dp[i][p].a=dp[i-1][p-nx].a+G[i][j].a;
// dp[i][p].b=dp[i-1][p-nx].b+G[i][j].b;
// dp[i][p].c=dp[i-1][p-nx].c+G[i][j].c;
// dp[i][p].d=dp[i-1][p-nx].d+G[i][j].d;
// }
if(tmp>dp[i][p].s){
dp[i][p].s=tmp;
dp[i][p].a=dp[i-1][p-nx].a+G[i][j].a;
dp[i][p].b=dp[i-1][p-nx].b+G[i][j].b;
dp[i][p].c=dp[i-1][p-nx].c+G[i][j].c;
dp[i][p].d=dp[i-1][p-nx].d+G[i][j].d;
}
}
}
}
}
ll ans=0;
rep(j,1,k)
for(int i=400;i<=sum;++i) {
ans=max(ans,dp[j][i].s);
//printf("i:%d dp:%lld %lld %lld %lld %lld\n",i,dp[k][i].s,dp[k][i].a,dp[k][i].b,dp[k][i].c,dp[k][i].d);
}
printf("%lld\n",ans);
rep(i,1,k) {
G[i].clear();
for(int j=0;j<=sum;++j) dp[i][j].up();
}
}
}
/*
10
3 2
1 10 10 10 10
1 20 0 0 20
2 0 20 20 0
*/
1012-String Distance
题意:给你s串(长度<=100000),t串(长度<=20),然后q次查询,每次查询区间l、r 问s串区间[l,r]内 对s串进行插入一个字符 或者 删除一个字符,求最小的操作次数 使得 能得到t串
做法: 虽然题意是区间最小编辑距离,但是却跟编辑距离没有一点关系,而是对区间内 求t串的最长公共子序列 r-l+1-|t|- 2*lcs 就是答案。然后 求最长公共子序列 用序列自动机 加速dp即可,设dp[i][j]为 t串前个字符,能跟s串有最长 j 的公共子序列时的 最小位置。
二维dp一下即可。
dp转移方程:
for(int i=1;i<=m;++i)
for(int j=0;j<=m;++j)
{
dp[i][j] = min(dp[i][j], dp[i-1][j]);
if(dp[i-1][j] > r) continue ;
if(nxt[dp[i-1][j]][t[i]-'a']<=r)
{
dp[i][j+1]=min(dp[i][j+1],nxt[dp[i-1][j]][t[i]-'a']);
}
}
AC代码:
#include
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define per(i,a,b) for(int i=a;i>=(b);--i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb emplace_back
#define pii pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
inline ll read()
{
ll x=0,w=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();}
return w==1?x:-x;
}
const int N=1e5+10;
char s[N],t[N];
int n,m;
int nxt[N][27],dp[30][30];
void init()
{
rep(i,0,25) nxt[n][i]=n+1;
for(int i=n;i>=1;--i){
for(int j=0;j<26;++j) nxt[i-1][j]=nxt[i][j];
nxt[i-1][s[i]-'a']=i;
}
//printf("nxxx %d\n",nxt[0]['w'-'a']);
}
int solve(int l,int r)
{
memset(dp,0x3f3f3f3f,sizeof(dp));
dp[0][0]=l-1;
for(int i=1;i<=m;++i)
for(int j=0;j<=m;++j)
{
dp[i][j] = min(dp[i][j], dp[i-1][j]);
if(dp[i-1][j] > r) continue ;
if(nxt[dp[i-1][j]][t[i]-'a']<=r)
{
dp[i][j+1]=min(dp[i][j+1],nxt[dp[i-1][j]][t[i]-'a']);
}
}
int ans=0;
for(int i=1;i<=m;++i)
for(int j=1;j<=i;++j)
if(dp[i][j] <= r) ans = max(ans, j);
return ans;
}
int main()
{
int _=read();while(_--){
scanf("%s%s",s+1,t+1);
n=strlen(s+1);
m=strlen(t+1);
init();
int q=read();while(q--){
int l=read(), r = read();
int len = solve(l,r);
//printf("len:%d\n",len);
int ans = r-l+1 + m - 2 * len;
printf("%d\n", ans);
}
}
}
/*
1
qaqaqwqaqaq
qaqwqaq
3
1 7
2 8
3 9
ans:
4
2
0
1
zzzz
abc
2
1 2
1 3
ans:
5
6
1
zzzz
zzz
2
1 2
1 3
1
azbdezc
acbde
1
1 7
ans:
4
*/