二叉树-常见题目

一、给定一个二叉树，找到该树中两个指定节点的最近公共祖先
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。

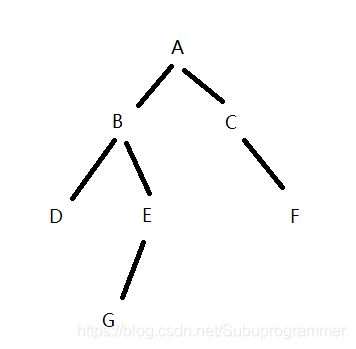
如上图，D和E的最近公共祖先就是B，G和F的最近公共祖先就是E，（一个节点也可以是自己的祖先）

//这个变量是最近公共节点
    private TreeNode Lac = null;

    //判断公共祖先
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) {
            return null;
        }
        findNode(root, p, q);
        return Lac;
    }

    //如果再root中能找到p或者q，就返回true,否则返回false
    private boolean findNode(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) {
            return false;
        }
        //查找：后序遍历形式进行查找
        int left = findNode(root.left, p, q) ? 1 : 0;
        int right = findNode(root.right, p, q) ? 1 : 0;
        //返回根节点
        int mid = (root == p || root == q) ? 1 : 0;

        if (left + right + mid == 2) {
            Lac = root;
        }

        return (left + right + mid) > 0;
    }

二、将二叉搜索树转成排序双向链表（二叉搜索树的中序遍历就是一个排好序的）

public class Solution {
        public TreeNode Convert(TreeNode root) {
        if (root == null) {
            return null;
        }
        if (root.left == null && root.right == null) {
            return root;
        }
        //先递归处理左子树,相当于把左子树已经完整的转换成双向链表，返回值为左子树链表的头节点
        TreeNode left = Convert(root.left);
        //根节点追加到左子树链表的末尾(链表尾插)
        //先找到链表的末尾(right相当于是next,left相当于prev)
        TreeNode leftTail = left;
        while (leftTail != null && leftTail.right != null) {
            leftTail = leftTail.right;
        }
        if (leftTail != null) {
            leftTail.right = root;
            root.left = leftTail;
        }


        //最后递归处理右子树(得到右子树的头节点）
        TreeNode right = Convert(root.right);
        if (right != null) {
            root.right = right;
            right.left = root;
        }
        //left不为空返回left，为空的话就返回right
        return left!=null?left:root;
    }
}

三、根据一棵树的前序遍历和中序遍历结构构建这棵二叉树

class Solution {
    private int index=0;
    public  TreeNode buildTree(int[] preorder, int[] inorder) {
        index=0;
        return buildTreeHelper(preorder,inorder,0,inorder.length);

    }

    private TreeNode buildTreeHelper(int[] preorder, int[] inorder, int inorderLeft, int inorderRight) {
        if(inorderLeft>=inorderRight){
            return null;
        }
        if(index>=inorder.length){
            return null;
        }
        TreeNode newNode=new TreeNode(preorder[index]);
        //左子树对应的中序区间  inorderLeft到pos结束，右子树对应的中序区间
        int pos=find(inorder,inorderLeft,inorderRight,newNode.val);
        index++;
        newNode.left=buildTreeHelper(preorder,inorder,inorderLeft,pos);
        newNode.right=buildTreeHelper(preorder,inorder,pos+1,inorderRight);
        return newNode;
    }

    private int find(int[] inorder, int inorderLeft, int inorderRight, int val) {
        for(int i=inorderLeft;i