Triose

并查集的几道题目

先从最简单的开始：

题意：一共n个强盗，m条线索，输出有多少个独立团伙（同伙的同伙是同伙，老鼠的儿子会打洞）

样例输入：

10 9

1 2

3 4

5 2

4 6

2 6

8 7

9 7

1 6

2 4

样例输出：

代码：

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
//#define ONLINE_JUDGE
#define eps 1e-8
#define INF 0x7fffffff                                            //INT_MAX
#define inf 0x3f3f3f3f                                            //int??????????????????
#define FOR(i,a) for((i)=0;i<(a);(i)++)                            //[i,a);
#define MEM(a) (memset((a),0,sizeof(a)))
#define sfs(a) scanf("%s",a)
#define sf(a) scanf("%d",&a)
#define sfI(a) scanf("%I64d",&a)
#define pf(a) printf("%d\n",a)
#define pfI(a) printf("%I64d\n",a)
#define pfs(a) printf("%s\n",a)
#define sfd(a,b) scanf("%d%d",&a,&b)
#define sft(a,b,c)scanf("%d%d%d",&a,&b,&c)
#define for1(i,a,b) for(int i=(a);i=a;i--)
#define MEM1(a) memset(a,0,sizeof(a))
#define MEM2(a) memset(a,-1,sizeof(a))
#define LL __int64
const double PI = acos(-1.0);
template T gcd(T a, T b) {return b ? gcd(b, a % b) : a;}
template T lcm(T a, T b) {return a / gcd(a, b) * b;}
template inline T Min(T a, T b) {return a < b ? a : b;}
template inline T Max(T a, T b) {return a > b ? a : b;}
using namespace std;
int n,m;
#define N 1010
int robber[N];
void Init(){						//初始化函数
	for(int i = 1; i <= n; i++){
		robber[i] = i;
	}
}
int getheader(int u){					//找爹函数
	if(robber[u] == u){
		return u;
	}
	else{
		return robber[u] = getheader(robber[u]);
	}
}
void merge(int u,int v){				//合并u，v强盗团伙的函数
	int t1,t2;
	t1 = getheader(u);
	t2 = getheader(v);
	if(t1 > t2){					//让标号比较大的强盗都归顺编号比较小的强盗
		t1 ^= t2;
		t2 ^= t1;
		t1 ^= t2;
	}
	if(t1 != t2){
		robber	[t2] = t1;
	}
}
int main(){
#ifndef ONLINE_JUDGE
//    freopen("in.txt","r",stdin);
//    freopen("out.txt","w",stdout);
#endif
	while(sfd(n,m) != EOF){
		Init();
		int r1,r2;
		for(int i = 0; i < m;i++){
			sfd(r1,r2);
			merge(r1,r2);
		}
		int num = 0;
		for(int i = 1; i <= n; i++){
			if(robber[i] == i)
				num++;
		}
		pf(num);
	}
    return 0;
}

没啥好总结的。。。

然后有变形。。。又是王教授出的。。

找朋友

时间限制(C/C++):1000MS/3000MS 运行内存限制:65536KByte
总提交:422 测试通过:138

描述

假设朋友关系是可以传递的，也就是说，如果A和B是朋友，B和C是朋友，那么A和C也是朋友。给出一个人员集合及其朋友关系，则这个集合可以分割成为不相交的子集合。给出一个人员的集合，以及他们之间部分的关系（哪两个人是朋友），让你求出分割出的子集合中最大的那个有多少人。

输入

第一行是一个整数，在[2,50]之间，表示要输入的案例的数量。对每个案例，第一行是2个整数，用空格隔开。第一个整数m表示集合的规模，第二个整数给出的关系数量n。后面紧跟n行，每一行都是两个整数x和y，满足0 <= x, y < n。0

输出

对每一个案例，输出该集合分割后最大的那个子集合中的人数。

样例输入

样例输出

4
3

这下好，还要统计人数。。用个结构体就ok

代码：

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
//#define ONLINE_JUDGE
#define eps 1e-8
#define INF 0x7fffffff                                            //INT_MAX
#define inf 0x3f3f3f3f                                            //int??????????????????
#define FOR(i,a) for((i)=0;i<(a);(i)++)                            //[i,a);
#define MEM(a) (memset((a),0,sizeof(a)))
#define sfs(a) scanf("%s",a)
#define sf(a) scanf("%d",&a)
#define sfI(a) scanf("%I64d",&a)
#define pf(a) printf("%d\n",a)
#define pfI(a) printf("%I64d\n",a)
#define pfs(a) printf("%s\n",a)
#define sfd(a,b) scanf("%d%d",&a,&b)
#define sft(a,b,c)scanf("%d%d%d",&a,&b,&c)
#define for1(i,a,b) for(int i=(a);i=a;i--)
#define MEM1(a) memset(a,0,sizeof(a))
#define MEM2(a) memset(a,-1,sizeof(a))
#define LL __int64
const double PI = acos(-1.0);
template T gcd(T a, T b) {return b ? gcd(b, a % b) : a;}
template T lcm(T a, T b) {return a / gcd(a, b) * b;}
template inline T Min(T a, T b) {return a < b ? a : b;}
template inline T Max(T a, T b) {return a > b ? a : b;}
using namespace std;
int n,m;
#define N 105
struct People{
    int header;
    int num;
};
People a[N];
void My_swap(int & a,int & b){
    a ^= b;     b ^= a;     a ^= b;
}
void Init(){
    for(int i = 0; i < n;i++){
        a[i].header = i;
        a[i].num = 1;
    }
}
int getheader(int t){
    if(a[t].header == t){
        return t;
    }
    else{
        return a[t].header = getheader(a[t].header);
    }
}
void merge(int u,int v){
    int t1,t2;
    t1 = getheader(u);
    t2 = getheader(v);
    if(t1 > t2){
        My_swap(t1,t2);				//其实这步并没有什么必要，好理解一点点
    }
    if(t1 != t2){
        a[t2].header = t1;
        a[t1].num += a[t2].num;
    }
}
int main(){
#ifndef ONLINE_JUDGE
//    freopen("in.txt","r",stdin);
//    freopen("out.txt","w",stdout);
#endif
    int t,x,y;
    sf(t);
    while(t--){
        sfd(n,m);
        Init();
        for(int i = 0; i < m; i++){
            sfd(x,y);
            merge(x,y);
        }
        int max_sum = 0;
        for(int i = 0; i < n; i++){
            max_sum = max_sum > a[i].num ? max_sum : a[i].num;
        }
        pf(max_sum);
    }
    return 0;
}

只是跑得慢了点。。。

还有一道变了变样子的题：

AQ and his xiaoqiang

时间限制(C/C++):1000MS/3000MS 运行内存限制:65536KByte
总提交:45 测试通过:8

描述

In AQ's dormitory,there are n xiaoqiang.They are so smart that they have their ways to know others as friends or enemies,
any two of them are friends or enemies if they know each other.And the relationship among them described as follows:
(we assume 3 xiaoqiang named A,B,C)
1.if A's friend is B,B's friend is C,so C is also a friend of A.
2.if A's enemy is B,B's enemy is C,so C is a friend of A.
We know a family consist of the xiaoqiang who are all friends between any two of them.So if I tell you
m relationships among n xiaoqiang,can you tell me what is the maximum number of families in AQ's dormitory?

输入

There are multiple cases.In the first line,there is n and m,represents the number of xiaoqiang and the relationships.(n<1000, m<5000)
among them.In the following m rows,there are three numbers:p x y.
1.p=1,x and y are friends.
2.p=0,x and y are enemies.

输出

Please output the maximum number of families in one line.

样例输入

样例输出

居然是小强我也是醉了，还有敌人啊朋友我也是醉了

代码：

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
//#define ONLINE_JUDGE
#define eps 1e-8
#define INF 0x7fffffff                                            //INT_MAX
#define inf 0x3f3f3f3f                                            //int??????????????????
#define FOR(i,a) for((i)=0;i<(a);(i)++)                            //[i,a);
#define MEM(a) (memset((a),0,sizeof(a)))
#define sfs(a) scanf("%s",a)
#define sf(a) scanf("%d",&a)
#define sfI(a) scanf("%I64d",&a)
#define pf(a) printf("%d\n",a)
#define pfI(a) printf("%I64d\n",a)
#define pfs(a) printf("%s\n",a)
#define sfd(a,b) scanf("%d%d",&a,&b)
#define sft(a,b,c)scanf("%d%d%d",&a,&b,&c)
#define for1(i,a,b) for(int i=(a);i=a;i--)
#define MEM1(a) memset(a,0,sizeof(a))
#define MEM2(a) memset(a,-1,sizeof(a))
#define LL __int64
const double PI = acos(-1.0);
template T gcd(T a, T b) {return b ? gcd(b, a % b) : a;}
template T lcm(T a, T b) {return a / gcd(a, b) * b;}
template inline T Min(T a, T b) {return a < b ? a : b;}
template inline T Max(T a, T b) {return a > b ? a : b;}
using namespace std;
int n,m;
#define N 1010
int a[N];
bool enem[N][N];
void Init(){
    memset(enem,false,sizeof(enem));
    for(int i = 0; i < N; i++)
        a[i] = i;
}
int geth(int t){
    if(a[t] == t){
        return t;
    }
    else{
        return a[t] = geth(a[t]);
    }
}
 
void merge(int u,int v){
    int t1 ,t2;
    t1 = geth(u);
    t2 = geth(v);
    if(t1 > t2){
        t1 ^= t2;
        t2 ^= t1;
        t1 ^= t2;
    }
    if(t1 != t2){
        a[t2] = t1;
    }
}
int main(){
    int p,x,y;
    while(sfd(n,m) != EOF){
        Init();
        for(int i = 0; i < m; i++){
            sft(p,x,y);
            if(p)
                merge(x,y);
            if(!p){
                enem[x][y] = true;            	//标记敌人
                enem[y][x] = true;		//一开始错就错在没加这句，既然是互为敌人那么两个都要标记！
            }
        }
        int temp = 0;
        for(int i = 1; i <= n; i++){
            for(int j = 1 ,indx = 0; j <= n; j++){
                if(enem[i][j] && indx == 0){
                    temp = j;			//第一个敌人和所有敌人都合并
                    indx++;
                }
                else if(enem[i][j]){
                    merge(temp,j);
                }
            }
        }
        int num = 0;
        for(int i = 1; i <= n; i++){
            if(a[i] == i)
                num++;
        }
        pf(num);
    }
    return 0;
}

这个算法还算比较简单。。

不过简单是简单当然有值得注意的地方

比如图中判断是否直接或者间接连接的问题时，例如CF的这道题

Mr. Kitayuta has just bought an undirected graph consisting of n vertices and m edges. The vertices of the graph are numbered from 1 ton. Each edge, namely edge i, has a color ci, connecting vertex ai and bi.

Mr. Kitayuta wants you to process the following q queries.

In the i-th query, he gives you two integers — ui and vi.

Find the number of the colors that satisfy the following condition: the edges of that color connect vertex ui and vertex vi directly or indirectly.

Input

The first line of the input contains space-separated two integers — n and m (2 ≤ n ≤ 100, 1 ≤ m ≤ 100), denoting the number of the vertices and the number of the edges, respectively.

The next m lines contain space-separated three integers — ai, bi (1 ≤ ai < bi ≤ n) and ci (1 ≤ ci ≤ m). Note that there can be multiple edges between two vertices. However, there are no multiple edges of the same color between two vertices, that is, if i ≠ j,(ai, bi, ci) ≠ (aj, bj, cj).

The next line contains a integer — q (1 ≤ q ≤ 100), denoting the number of the queries.

Then follows q lines, containing space-separated two integers — ui and vi (1 ≤ ui, vi ≤ n). It is guaranteed that ui ≠ vi.

Output

For each query, print the answer in a separate line.

     Sample test(s) 
   

       input 
     
4 5
1 2 1
1 2 2
2 3 1
2 3 3
2 4 3
3
1 2
3 4
1 4

       output 
     
2
1
0

       input 
     
5 7
1 5 1
2 5 1
3 5 1
4 5 1
1 2 2
2 3 2
3 4 2
5
1 5
5 1
2 5
1 5
1 4

       output 
     
1
1
1
1
2

Note

Let's consider the first sample.

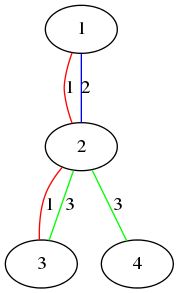$并查集的几道题目_第1张图片$ The figure above shows the first sample.

Vertex 1 and vertex 2 are connected by color 1 and 2.
Vertex 3 and vertex 4 are connected by color 3.
Vertex 1 and vertex 4 are not connected by any single color.

再例如这组数据：

5 4
2 3 1
2 5 1
2 4 1
2 1 1
4
1 2
1 3
1 4
1 5

通过合并先后把 (2,3) (2,5) (2,4) (2,1) 终点都是1这个点（通过颜色1连接）但是 3,4,5这三个点的终点并不是1，而是2，这就是这道题一直错的原因

说多了都是泪贴代码！

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
//#define ONLINE_JUDGE
#define eps 1e-8
#define INF 0x7fffffff											//INT_MAX
#define inf 0x3f3f3f3f    										//int范围内可靠的无穷大
#define FOR(i,a) for((i)=0;i<(a);(i)++)							//
#define MEM(a) (memset((a),0,sizeof(a)))
#define sfs(a) scanf("%s",a)
#define sf(a) scanf("%d",&a)
#define sfI(a) scanf("%I64d",&a)
#define pf(a) printf("%d\n",a)
#define pfI(a) printf("%I64d\n",a)
#define pfs(a) printf("%s\n",a)
#define sfd(a,b) scanf("%d%d",&a,&b)
#define sft(a,b,c)scanf("%d%d%d",&a,&b,&c)
#define for1(i,a,b) for(int i=(a);i=a;i--)
#define MEM1(a) memset(a,0,sizeof(a))
#define MEM2(a) memset(a,-1,sizeof(a))
#define LL __int64
const double PI=acos(-1.0);
template T gcd(T a,T b){return b?gcd(b,a%b):a;}
template T lcm(T a,T b){return a/gcd(a,b)*b;}
template inline T Min(T a,T b){return a inline T Max(T a,T b){return a>b?a:b;}
using namespace std;
int n,m,q;
#define N 110
int pic[N][N];
int num = 0;
int get_head(int p,int c){
	return pic[p][c] == p ? p : pic[p][c] = get_head(pic[p][c],c);
}
void merge(int p1,int p2,int c){
	int h1 = get_head(p1,c);
	int h2 = get_head(p2,c);
	if(h1 != h2){
		pic[h1 < h2 ? pic[p2][c] : pic[p1][c]][c] = h1 < h2 ? h1 : h2;
	}
}
void Init(){
	int point_1,point_2,color;
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++){
			pic[i][j] = i;
		}
	}
	for(int i = 0; i < m; i++){
		sft(point_1,point_2,color);
		merge(point_1,point_2,color);
	}
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++){
			pic[i][j] = get_head(pic[i][j],j);
		}
	}
}
void slove(){
	sf(q);
	int x,y;
	while(q--){
		num = 0;
		sfd(x,y);
		for(int i = 1; i <= m; i++){
			if(pic[x][i] == pic[y][i])
				num++;
		}
		pf(num);
	}
}
int main(){
#ifndef ONLINE_JUDGE
	freopen("in.txt","r",stdin);
//	freopen("Out.txt","w",stdout);
#endif
	while(~sfd(n,m)){
		Init();
		slove();
	}
	return 0;
}

⭐算法入门⭐《归并排序》简单01 —— LeetCode 21. 合并两个有序链表英雄哪里出来《LeetCode算法全集》算法数据结构链表 c++归并排序
饭不食，水不饮，题必须刷C语言免费动漫教程，和我一起打卡！《光天化日学C语言》LeetCode太难？先看简单题！《C语言入门100例》数据结构难？不存在的！《数据结构入门》LeetCode太简单？算法学起来！《夜深人静写算法》文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识一、题目1、题目描述将两个不降序链表合并为一个新的不降
ABC371 解题报告（A-E） Plossom 赛后总结深度优先算法 c++贪心算法图论性能优化
A题意给定A,B之间，B,C之间，A,C之间的不等关系（大于或小于），问A,B,C中排第二大的数是哪一个。解法乍一看没啥思路，原来正解是打表（8种情况秒了）。 if(a==""){ cout"&&c==""&&c==">"){ cout"&&b==""&&b==""){ cout"&&b==">"&&c==""&&b==">"&&c==">"){ cout>n>
牛客周赛 Round 13 解题报告 | 珂学家 | 乘法原理场 + BFS上组合 + 众数贪心 Buoluochuixue java
题解|#简单计算器##includeintmain(){doublea,b;charoperate;scanf(&迈瑞医疗一面等了面试官十几分钟，更气人在后面上来自我介绍完了就让开始做题。。。题不算很难，做完了之后，讲了下思路，后面根据简历提问。一分钟简单介绍下实习做的东西，我说到一半经纬恒润Java开发一面时长：35min1.聊项目2.gc3.线程共享私有4.类加载过程5.I/O相关6.Spri
[leetcode] 408. Valid Word Abbreviation 解题报告小榕流光 leetcode string leetcode string
题目链接：https://leetcode.com/problems/valid-word-abbreviation/Givenanon-emptystringsandanabbreviationabbr,returnwhetherthestringmatcheswiththegivenabbreviation.Astringsuchas
LeetCode 剑指 Offer II 093. 最长斐波那契数列大涛小先生 LeetCode解题报告 leetcode 算法动态规划
LeetCode剑指OfferII093.最长斐波那契数列文章目录LeetCode剑指OfferII093.最长斐波那契数列题目描述一、解题关键词二、解题报告1.思路分析2.时间复杂度3.代码示例2.知识点总结相同题目题目描述如果序列X_1,X_2,…,X_n满足下列条件，就说它是斐波那契式的：n>=3对于所有i+2<=n，都有X_i+X_{i+1}=X_{i+2}给定一个严格递增的正整数数组形成
单调栈 LeetCode 1130. 叶值的最小代价生成树 EQUINOX1 OJ刷题解题报告 leetcode 算法动态规划
目录一、题目1、题目描述2、输入输出2.1输入2.2输出3、原题链接二、解题报告1、思路分析2、复杂度3、代码详解一、题目1、题目描述给你一个正整数数组arr，考虑所有满足以下条件的二叉树：每个节点都有0个或是2个子节点。数组arr中的值与树的中序遍历中每个叶节点的值一一对应。每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。在所有这样的二叉树中，返回每个非叶节点的值的最小可能总和。这个
牛客周赛 Round 51 解题报告 | 珂学家珂朵莉酱牛客周赛解题报告算法 leetcode 职场和发展 java 开发语言
前言题解典题场，EF都有很多种解法A.小红的同余性质:相邻两数互质x=(m+1)/2x=(m+1)/2x=(m+1)/2m=int(input())print((m+1)//2)B.小红的三倍数性质:各个位数之和是3的倍数，可被3整除和数的组合顺序无关n=int(input())arr=list(map(int,input().split()))res=0forvinarr:whilev>0:re
牛客周赛 Round 48 解题报告 | 珂学家珂朵莉酱牛客周赛解题报告 leetcode 算法职场和发展 java python
前言题解这场感觉有点难，D完全没思路,EF很典，能够学到知识.E我的思路是容斥+贡献，F很典，上周考过一次，引入虚拟节点质数(有点像种类并查集类似的技巧).欢迎关注珂朵莉牛客周赛专栏珂朵莉牛客小白月赛专栏A.小红的整数自增题型:签到贪心即可，所以值往最大值靠拢即可arr=list(map(int,input().split()))z=max(arr)res=0forvinarr:res+=(z-v
牛客周赛 Round 19 解题报告 | 珂学家珂朵莉酱牛客周赛解题报告算法
前言整体评价这场挺有意思的，尤其是T4，其实很早之前也想过这个问题？如何智能的扫雷，感觉有点难。这题被逼得主动去求解这个扫雷问题，幸好只有4*4，可以暴力枚举。喜欢这种比赛。A.小红的字符串大小写变换Q:API题，把前k个字符大写，后n-k个字符小写可以切分为2段，然后分别大写，小写化，然后拼接即可importjava.io.BufferedInputStream;importjava.util.
牛客周赛 Round 47 解题报告 | 珂学家珂朵莉酱牛客周赛解题报告算法 leetcode 职场和发展 java 开发语言
前言题解这真的是牛客周赛？哭了欢迎关注珂朵莉牛客周赛专栏珂朵莉牛客小白月赛专栏A.小红的葫芦签到题但是写起来有点变扭，方法应该蛮多的统计分组有2组一组长度为2，一组长度为3defcheck(arr):arr.sort()ifarr[0]==arr[4]:returnFalseifarr[0]==arr[1]andarr[2]==arr[4]:returnTrueifarr[0]==arr[2]an
上岸算法 | LeetCode Weekly Contest 第 256 场周赛解题报告上岸算法
【NO.1学生分数的最小差值】解题思路排序，然后枚举每连续的K个元素即可。代码展示classSolution{publicintminimumDifference(int[]nums,intk){if(nums.length{if(a.length()!=b.length()){returnb.length()-a.length();}for(inti=0;i=0){returnmem[i];}m
牛客周赛 Round 32 解题报告 | 珂学家 | 状压 + 前缀和&异或map技巧珂朵莉MM 牛客周赛解题报告 java 算法力扣 leetcode 开发语言
前言整体评价属于补题，大致看了下，题都很典。欢迎关注珂朵莉牛客周赛专栏珂朵莉牛客小白月赛专栏A.小红的01背包思路:数学题v,x,y=list(map(int,input().split()))print(v//x*y)B.小红的dfs思路:枚举其实横竖都有dfs字符，只有3种情况第一行，第一列为dfs第二行，第二列为dfs第三行，第三列为dfs枚举取最小代价即可grids=[]foriinran
力扣第 384 场周赛解题报告 | 珂学家 | 贪心构造 + KMP板子珂朵莉MM 力扣周赛解题报告 leetcode 算法职场和发展 java 开发语言矩阵
前言整体评价因为是新春过年，所以题目出的相对简单一些，T4和上周一样，是字符串匹配模板题。T1.修改矩阵思路:模拟按要求模拟即可classSolution{publicint[][]modifiedMatrix(int[][]matrix){inth=matrix.length;intw=matrix[0].length;int[]cols=newint[w];Arrays.fill(cols,I
上岸算法 I LeetCode Weekly Contest 219解题报告上岸算法
No.1比赛中的配对次数解题思路模拟过程即可，较简单。代码展示classSolution{publicintnumberOfMatches(intn){intres=0;while(n>1){res+=n/2;n=(n+1)/2;}returnres;}}No.2十-二进制数的最少数目解题思路取决于最大的数字是多少。代码展示classSolution{publicintminPartitions(
[Leetcode] 741. Cherry Pickup 解题报告魔豆Magicbean IT公司面试习题 Leetcode 解题报告 Dynamic Programming
题目：InaNxNgridrepresentingafieldofcherries,eachcellisoneofthreepossibleintegers.0meansthecellisempty,soyoucanpassthrough;1meansthecellcontainsacherry,thatyoucanpickupandpassthrough;-1meansthecellcontai
牛客周赛 Round 8 解题报告 | 珂学家 | 构造 + 树形DP huaxinjiayou java
题解|#牛牛队列成环#本题知识点分析:1.链表前驱结点和后继结点2.链表遍历3.快慢指针本题解题思路分析：1.利用慢指针走一步，快指针走两步2.遍历同时判断两个指针的值是否相等，如果题解|#草原上的牛群#/***代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可***@paramnumsint整型一维数组*@retu题解|#牛群分隔#该题考察的知识点包括：单链表的遍历和操作：
LeetCode 2044. 统计按位或能得到最大值的子集数目英雄哪里出来《LeetCode算法全集》算法数据结构位运算
文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识四、加群须知一、题目1、题目描述给你一个整数数组nums，请你找出nums子集按位或可能得到的最大值，并返回按位或能得到最大值的不同非空子集的数目。样例输入：nums=[3,1] 样例输出：22、基础框架C语言版本给出的基础框架代码如下：intcountMaxOrSubse
LeetCode 2166. 设计位集英雄哪里出来《LeetCode算法全集》算法数据结构位运算异或
文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解1）核心代码2）全部代码三、本题小知识四、加群须知一、题目1、题目描述位集Bitset是一种能以紧凑形式存储位的数据结构。请你实现Bitset类。Bitset(intsize)用size个位初始化Bitset，所有位都是0。voidfix(intidx)将下标为idx的位上的值更新为1。如果值
LeetCode 2135. 统计追加字母可以获得的单词数英雄哪里出来《LeetCode算法全集》算法数据结构字符串状态压缩位运算
文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识四、加群须知一、题目1、题目描述给你两个下标从0开始的字符串数组startWords和targetWords。每个字符串都仅由小写英文字母组成。对于targetWords中的每个字符串，检查是否能够从startWords中选出一个字符串，执行一次转换操作，得到的结果与当前targ
LeetCode 6033. 转换数字的最少位翻转次数英雄哪里出来《LeetCode算法全集》算法数据结构位运算异或汉明距离
文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识四、加群须知一、题目1、题目描述一次位翻转定义为将数字x二进制中的一个位进行翻转操作，即将0变成1，或者将1变成0。给你两个整数start和goal，请你返回将start转变成goal的最少位翻转次数。样例输入：start=10,goal=7 样例输出：32、基础框架C语言
⭐算法入门⭐《广度优先搜索》中等01 —— LeetCode 994. 腐烂的橘子英雄哪里出来《LeetCode算法全集》算法数据结构队列 leetcode 广度优先搜索
饭不食，水不饮，题必须刷C语言免费动漫教程，和我一起打卡！《光天化日学C语言》LeetCode太难？先看简单题！《C语言入门100例》数据结构难？不存在的！《数据结构入门》LeetCode太简单？算法学起来！《夜深人静写算法》文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识四、加群须知一、题目1、题目描述在给定的网格中，每个单元格
⭐算法入门⭐《广度优先搜索》简单01 —— LeetCode 542. 01 矩阵英雄哪里出来《LeetCode算法全集》算法数据结构 c++leetcode 广度优先搜索
饭不食，水不饮，题必须刷C语言免费动漫教程，和我一起打卡！《光天化日学C语言》LeetCode太难？先看简单题！《C语言入门100例》数据结构难？不存在的！《数据结构入门》LeetCode太简单？算法学起来！《夜深人静写算法》文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识四、加群须知一、题目1、题目描述给定一个由0和1组成的
力扣第 383 场周赛解题报告 | KMP 上烟雨心上尘题解 leetcode 算法职场和发展
力扣第383场周赛解题报告|KMP链接前言一个人能走的多远不在于他在顺境时能走的多快，而在于他在逆境时多久能找到曾经的自己。T1修改矩阵思路：模拟时间复杂度：O(mn)O(mn)O(mn)classSolution:defmodifiedMatrix(self,matrix:List[List[int]])->List[List[int]]:n,m=len(matrix),len(matrix[0
经典递归，LeetCode 236. 二叉树的最近公共祖先 EQUINOX1 leetcode每日一题算法 leetcode c++数据结构
目录一、题目1、题目描述2、接口描述3、原题链接二、解题报告1、思路分析2、复杂度3、代码详解一、题目1、题目描述百度百科中最近公共祖先的定义为：“对于有根树T的两个节点p、q，最近公共祖先表示为一个节点x，满足x是p、q的祖先且x的深度尽可能大（一个节点也可以是它自己的祖先）。”2、接口描述/***Definitionforabinarytreenode.*structTreeNode{*in
层序遍历，LeetCode 993. 二叉树的堂兄弟节点 EQUINOX1 leetcode每日一题算法 c++职场和发展数据结构 leetcode
目录一、题目1、题目描述2、接口描述3、原题链接二、解题报告1、思路分析2、复杂度3、代码详解一、题目1、题目描述在二叉树中，根节点位于深度0处，每个深度为k的节点的子节点位于深度k+1处。如果二叉树的两个节点深度相同，但父节点不同，则它们是一对堂兄弟节点。我们给出了具有唯一值的二叉树的根节点root，以及树中两个不同节点的值x和y。只有与值x和y对应的节点是堂兄弟节点时，才返回true。否则，返
⭐算法入门⭐《二分枚举》中等05 —— LeetCode 1201. 丑数 III 英雄哪里出来《LeetCode算法全集》算法 leetcode
文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识四、加群须知一、题目1、题目描述给你四个整数：n、a、b、c，请你设计一个算法来找出第n个丑数。丑数是可以被a或b或c整除的正整数。样例输入：n=5,a=2,b=11,c=13 样例输出：102、基础框架C语言版本给出的基础框架代码如下：intnthUglyNumber(i
力扣第 383 场周赛解题报告 | 珂学家 | Z函数/StringHash 珂朵莉MM 力扣周赛解题报告 leetcode 算法职场和发展力扣 java python
前言谁言别后终无悔寒月清宵绮梦回深知身在情长在前尘不共彩云飞整体评价T3是道模拟题，但是感觉题意有些晦涩，T4一眼Z函数，当然StringHash更通用些。新年快乐,_.T1.将单词恢复初始状态所需的最短时间I思路:模拟就是前缀和为0的次数classSolution{publicintreturnToBoundaryCount(int[]nums){intacc=0;intres=0;for(in
牛客周赛 Round 31 解题报告 | 珂学家 | 设计 + 组合珂朵莉MM 牛客周赛解题报告 java 开发语言算法 leetcode 力扣
前言整体评价D题出的蛮好的，其实做过LruCache题的同学，基本都会，即Map+双向链表技巧。E题典型的DP题，负数可以引入偏移来解决。F题是道数学题，组合+乘法原理。欢迎关注珂朵莉牛客周赛专栏珂朵莉牛客小白月赛专栏A.小红小紫替换思路:模拟s=input()ifs=="kou":print("yukari")else:print(s)B.小红的因子数思路:质因子拆解x=int(input())
Acwing 141 周赛解题报告 | 珂学家 | 逆序数+奇偶性分析珂朵莉MM Acwing周赛解题报告 java 开发语言算法矩阵线性代数
前言整体评价很普通的一场比赛，t2思维题，初做时愣了下，幸好反应过来了。t3猜猜乐，感觉和逆序数有关，和奇偶性有关。不过要注意int溢出。欢迎关注:珂朵莉的天空之城A.客人数量题型:签到累加和即可importjava.io.BufferedInputStream;importjava.util.Scanner;publicclassMain{publicstaticvoidmain(String[
力扣第 123 场双周赛解题报告 | 珂学家 | 二维偏序+单调队列优化珂朵莉MM 力扣周赛解题报告 leetcode 算法职场和发展 java 开发语言力扣
前言执手看歌敲金钗，笑语落珠明眸睐。忽然蝴蝶春风满，焉教冷镜瘦朱颜。整体评价T3是基于map的前缀和的变形题，T4是二维偏序的一道应用题。题外话，力扣还是实现N久之前的承诺了，命名权奖励，赞一个。T1.三角形类型II思路:模拟classSolution{publicStringtriangleType(int[]nums){//先判合法性Arrays.sort(nums);if(nums[0]+n
深入浅出Java Annotation(元注解和自定义注解） Josh_Persistence Java Annotation 元注解自定义注解
一、基本概述　　 Annontation是Java5开始引入的新特征。中文名称一般叫注解。它提供了一种安全的类似注释的机制，用来将任何的信息或元数据（metadata）与程序元素（类、方法、成员变量等）进行关联。　　更通俗的意思是为程序的元素（类、方法、成员变量）加上更直观更明了的说明，这些说明信息是与程序的业务逻辑无关，并且是供指定的工具或
mysql优化特定类型的查询 annan211 java 工作 mysql
本节所介绍的查询优化的技巧都是和特定版本相关的，所以对于未来mysql的版本未必适用。 1 优化count查询对于count这个函数的网上的大部分资料都是错误的或者是理解的都是一知半解的。在做优化之前我们先来看看真正的count()函数的作用到底是什么。 count()是一个特殊的函数，有两种非常不同的作用，他可以统计某个列值的数量，也可以统计行数。在统
MAC下安装多版本JDK和切换几种方式棋子chessman jdk
环境： MAC AIR,OS X 10.10,64位历史：过去 Mac 上的 Java 都是由 Apple 自己提供，只支持到 Java 6，并且OS X 10.7 开始系统并不自带（而是可选安装）（原自带的是1.6）。后来 Apple 加入 OpenJDK 继续支持 Java 6，而 Java 7 将由 Oracle 负责提供。在终端中输入jav
javaScript （1） Array_06 JavaScript java 浏览器
JavaScript 1、运算符　　运算符就是完成操作的一系列符号，它有七类：　　赋值运算符（=,+=,-=,*=,/=,%=,<<=,>>=,|=,&=）、算术运算符(+,-,*,/,++,--,%)、比较运算符(>,<,<=,>=,==,===,!=,!==)、逻辑运算符(||,&&,!)、条件运算(?:)、位
国内顶级代码分享网站袁潇含 java jdk oracle .net PHP
现在国内很多开源网站感觉都是为了利益而做的当然利益是肯定的,否则谁也不会免费的去做网站 &
Elasticsearch、MongoDB和Hadoop比较随意而生 mongodb hadoop 搜索引擎
IT界在过去几年中出现了一个有趣的现象。很多新的技术出现并立即拥抱了“大数据”。稍微老一点的技术也会将大数据添进自己的特性，避免落大部队太远，我们看到了不同技术之间的边际的模糊化。假如你有诸如Elasticsearch或者Solr这样的搜索引擎，它们存储着JSON文档，MongoDB存着JSON文档，或者一堆JSON文档存放在一个Hadoop集群的HDFS中。你可以使用这三种配
mac os 系统科研软件总结张亚雄 mac os
1.1 Microsoft Office for Mac 2011 大客户版，自行搜索。 1.2 Latex （MacTex）: 系统环境：https://tug.org/mactex/ &nb
Maven实战（四）生命周期 AdyZhang maven
1. 三套生命周期 Maven拥有三套相互独立的生命周期，它们分别为clean，default和site。每个生命周期包含一些阶段，这些阶段是有顺序的，并且后面的阶段依赖于前面的阶段，用户和Maven最直接的交互方式就是调用这些生命周期阶段。以clean生命周期为例，它包含的阶段有pre-clean, clean 和 post
Linux下Jenkins迁移 aijuans Jenkins
1. 将Jenkins程序目录copy过去源程序在/export/data/tomcatRoot/ofctest-jenkins.jd.com下面 tar -cvzf jenkins.tar.gz ofctest-jenkins.jd.com &
request.getInputStream()只能获取一次的问题 ayaoxinchao request Inputstream
问题：在使用HTTP协议实现应用间接口通信时，服务端读取客户端请求过来的数据，会用到request.getInputStream()，第一次读取的时候可以读取到数据，但是接下来的读取操作都读取不到数据原因： 1. 一个InputStream对象在被读取完成后，将无法被再次读取，始终返回-1； 2. InputStream并没有实现reset方法（可以重
数据库SQL优化大总结之百万级数据库优化方案 BigBird2012 SQL优化
网上关于SQL优化的教程很多，但是比较杂乱。近日有空整理了一下，写出来跟大家分享一下，其中有错误和不足的地方，还请大家纠正补充。这篇文章我花费了大量的时间查找资料、修改、排版，希望大家阅读之后，感觉好的话推荐给更多的人，让更多的人看到、纠正以及补充。 1.对查询进行优化，要尽量避免全表扫描，首先应考虑在 where 及 order by 涉及的列上建立索引。 2.应尽量避免在 where
jsonObject的使用 bijian1013 java json
在项目中难免会用java处理json格式的数据，因此封装了一个JSONUtil工具类。 JSONUtil.java package com.bijian.json.study; import java.util.ArrayList; import java.util.Date; import java.util.HashMap;
[Zookeeper学习笔记之六]Zookeeper源代码分析之Zookeeper.WatchRegistration bit1129 zookeeper
Zookeeper类是Zookeeper提供给用户访问Zookeeper service的主要API，它包含了如下几个内部类首先分析它的内部类，从WatchRegistration开始，为指定的znode path注册一个Watcher， /** * Register a watcher for a particular p
【Scala十三】Scala核心七：部分应用函数 bit1129 scala
何为部分应用函数？ Partially applied function: A function that’s used in an expression and that misses some of its arguments.For instance, if function f has type Int => Int => Int, then f and f(1) are p
Tomcat Error listenerStart 终极大法 ronin47 tomcat
Tomcat报的错太含糊了，什么错都没报出来，只提示了Error listenerStart。为了调试，我们要获得更详细的日志。可以在WEB-INF/classes目录下新建一个文件叫logging.properties，内容如下 Java代码 handlers = org.apache.juli.FileHandler, java.util.logging.ConsoleHa
不用加减符号实现加减法 BrokenDreams 实现
今天有群友发了一个问题，要求不用加减符号(包括负号)来实现加减法。分析一下，先看最简单的情况，假设1+1，按二进制算的话结果是10，可以看到从右往左的第一位变为0，第二位由于进位变为1。
读《研磨设计模式》-代码笔记-状态模式-State bylijinnan java 设计模式
声明：本文只为方便我个人查阅和理解，详细的分析以及源代码请移步原作者的博客http://chjavach.iteye.com/ /* 当一个对象的内在状态改变时允许改变其行为，这个对象看起来像是改变了其类状态模式主要解决的是当控制一个对象状态的条件表达式过于复杂时的情况把状态的判断逻辑转移到表示不同状态的一系列类中，可以把复杂的判断逻辑简化如果在
CUDA程序block和thread超出硬件允许值时的异常 cherishLC CUDA
调用CUDA的核函数时指定block 和 thread大小，该大小可以是dim3类型的（三维数组），只用一维时可以是usigned int型的。以下程序验证了当block或thread大小超出硬件允许值时会产生异常！！！GPU根本不会执行运算！！！所以验证结果的正确性很重要！！！在VS中创建CUDA项目会有一个模板，里面有更详细的状态验证。以下程序在K5000GPU上跑的。
诡异的超长时间GC问题定位 chenchao051 jvm cms GC hbase swap
HBase的GC策略采用PawNew+CMS, 这是大众化的配置，ParNew经常会出现停顿时间特别长的情况，有时候甚至长到令人发指的地步，例如请看如下日志： 2012-10-17T05:54:54.293+0800: 739594.224: [GC 739606.508: [ParNew: 996800K->110720K(996800K), 178.8826900 secs] 3700
maven环境快速搭建 daizj 安装 mavne 环境配置
一下载maven 安装maven之前，要先安装jdk及配置JAVA_HOME环境变量。这个安装和配置java环境不用多说。 maven下载地址：http://maven.apache.org/download.html，目前最新的是这个apache-maven-3.2.5-bin.zip，然后解压在任意位置，最好地址中不要带中文字符，这个做java 的都知道，地址中出现中文会出现很多
PHP网站安全，避免PHP网站受到攻击的方法 dcj3sjt126com PHP
对于PHP网站安全主要存在这样几种攻击方式:1、命令注入(Command Injection)2、eval注入(Eval Injection)3、客户端脚本攻击(Script Insertion)4、跨网站脚本攻击(Cross Site Scripting, XSS)5、SQL注入攻击(SQL injection)6、跨网站请求伪造攻击(Cross Site Request Forgerie
yii中给CGridView设置默认的排序根据时间倒序的方法 dcj3sjt126com GridView
public function searchWithRelated() { $criteria = new CDbCriteria; $criteria->together = true; //without th
Java集合对象和数组对象的转换 dyy_gusi java集合
在开发中，我们经常需要将集合对象（List，Set）转换为数组对象，或者将数组对象转换为集合对象。Java提供了相互转换的工具，但是我们使用的时候需要注意，不能乱用滥用。 1、数组对象转换为集合对象最暴力的方式是new一个集合对象，然后遍历数组，依次将数组中的元素放入到新的集合中，但是这样做显然过
nginx同一主机部署多个应用 geeksun nginx
近日有一需求，需要在一台主机上用nginx部署2个php应用，分别是wordpress和wiki，探索了半天，终于部署好了，下面把过程记录下来。 1. 在nginx下创建vhosts目录，用以放置vhost文件。 mkdir vhosts 2. 修改nginx.conf的配置，在http节点增加下面内容设置，用来包含vhosts里的配置文件 #
ubuntu添加admin权限的用户账号 hongtoushizi ubuntu useradd
ubuntu创建账号的方式通常用到两种：useradd 和adduser . 本人尝试了useradd方法，步骤如下： 1:useradd 使用useradd时，如果后面不加任何参数的话，如：sudo useradd sysadm 创建出来的用户将是默认的三无用户：无home directory ,无密码,无系统shell。顾应该如下操作：
第五章常用Lua开发库2-JSON库、编码转换、字符串处理 jinnianshilongnian nginx lua
JSON库在进行数据传输时JSON格式目前应用广泛，因此从Lua对象与JSON字符串之间相互转换是一个非常常见的功能；目前Lua也有几个JSON库，本人用过cjson、dkjson。其中cjson的语法严格（比如unicode \u0020\u7eaf），要求符合规范否则会解析失败（如\u002），而dkjson相对宽松，当然也可以通过修改cjson的源码来完成
Spring定时器配置的两种实现方式OpenSymphony Quartz和java Timer详解 yaerfeng1989 timer quartz 定时器
原创整理不易，转载请注明出处：Spring定时器配置的两种实现方式OpenSymphony Quartz和java Timer详解代码下载地址：http://www.zuidaima.com/share/1772648445103104.htm 有两种流行Spring定时器配置：Java的Timer类和OpenSymphony的Quartz。 1.Java Timer定时首先继承jav
Linux下df与du两个命令的差别？ pda158 linux
　一、df显示文件系统的使用情况，与du比較，就是更全盘化。　　最经常使用的就是 df -T，显示文件系统的使用情况并显示文件系统的类型。　　举比例如以下：　　[root@localhost ~]# df -T 　　Filesystem Type &n
[转]SQLite的工具类 ---- 通过反射把Cursor封装到VO对象 ctfzh VO android sqlite 反射 Cursor
在写DAO层时，觉得从Cursor里一个一个的取出字段值再装到VO(值对象)里太麻烦了，就写了一个工具类，用到了反射，可以把查询记录的值装到对应的VO里，也可以生成该VO的List。使用时需要注意：考虑到Android的性能问题，VO没有使用Setter和Getter，而是直接用public的属性。表中的字段名需要和VO的属性名一样，要是不一样就得在查询的SQL中
该学习笔记用到的Employee表 vipbooks oracle sql 工作
这是我在学习Oracle是用到的Employee表，在该笔记中用到的就是这张表，大家可以用它来学习和练习。 drop table Employee; -- 员工信息表 create table Employee( -- 员工编号 EmpNo number(3) primary key, -- 姓

并查集的几道题目

找朋友

AQ and his xiaoqiang

你可能感兴趣的:(解题报告)