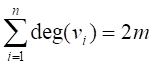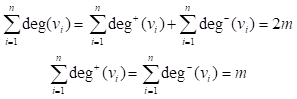《离散数学》期末复习笔记
一、图及其图解表示
定义 7.1 一个图G是一个有序二元组(V,E),记作G = (V,E),其中V = {v1,v2,…,vn}是一个非空的有限集合,V中的元素称为G的结点或顶点,V称为图G的结点集,记作V(G)。
E = {e1,e2,…,em}是一个由V中元素构成的对偶的集合,E中的元素称为G的边或弧,E称为图G的边集,记作E(G)。
#V(G),#E(G)分别称为图的结点数和边数。
图的结点数也称为图的阶,n个结点的图称为n阶图。
具有n个结点和m条边的图称为(n,m)图。
(n,0)图称为零图。
(1,0)图称为平凡图。
定义 7.2 图G = (V,E)中,
若E的元素e为V中两个元素u和v的非有序的对偶,则称边e为图G的无向边,记为e = {u,v},其中,结点u和v称为无向边e的端点;
若E的元素e为V中两个元素u和v的有序的对偶,则称边e为图G的有向边,记为e = (u,v),其中,结点u和v分别称为有向边e的起点(或始点)和终点,也称为有向边的端点。
以结点u为端点的边称为结点u的关联边。
定义 7.3 图G = (V,E)中,端点相同的边{u,u}或(u,u)称为结点u的自环。
E中相同的边{u,v}或(u,v)称为平行边或重复边,
并称重复边的条数为该边的重数。
定义 7.4 图G = (V,E)中,含有平行边的图称为多重图。
既不含自环又不含平行边的图称为简单图。
定义 7.5 所有边都是无向边的图称为无向图,所有边都是无向边的简单图称为无向简单图。
所有边都是有向边的图称为有向图,所有边都是有向边的简单图称为有向简单图。
既含无向边又含有向边的图称为混合图。
定义 7.6 将有向图的各条有向边略去方向后所得到的无向图称为该有向图的基础图,简称基图。
如果将无向图的各条边任意定一个方向后所得到的有向图称为该无向图的一个定向图。
定义 7.7 如果图G的每条边都赋以一个实数作为该边的权,则称图G为赋权图或有权图。
有权图可定义为一个有序三元组(V,E,f ),其中 f 是一个定义在边集E上的函数,通过 f 将权分配给各边。
定义 7.8 图中关联于同一条边的两个结点称为是邻接点,关联于同一结点的两条边称为是邻接边。
图中不与其他任何结点相邻接的结点称为是孤立点,不与其他任何边相邻接的边称为是孤立边。
零图是仅由孤立结点组成的图。
平凡图是仅由一个孤立结点组成的图。
二、完全图与补图
定义 7.9 在无向简单图中,如果任意两个不同的结点都是邻接的,则称该图是无向完全图。n 个结点的完全图记作 Kn。
在有向简单图中,如果任意两个不同的结点之间均有两条方向相反的有向边,则称该有向图为有向完全图。
在有向简单图中,如果任意两个不同的结点之间有且仅有一条有向边,则称该有向图为竞赛图。
例如:无向完全图的一个定向图就是一个竞赛图。
注意:
n阶无向完全图的边数m = n(n – 1)/2。
n阶有向竞赛图的边数m = n(n – 1)/2。
n阶有向完全图的边数m = n(n – 1)。
定义 7.10 设G是一个简单图,由G的所有结点和为了使G成为完全图所需添加的那些边组成的图,称为G的相对于完全图的补图,简称为G的补图,一般用![]() 表示。
表示。
图G与![]() 互为补图。
互为补图。
三、结点的度与握手定理
定义 7.11 图中关联于结点v的边的总数称为该结点的度,记作deg(v)。
在有向图中,
以v为起点的有向边的条数称为结点v的出度,记作deg+(v)。
以v为终点的有向边的条数称为结点v的入度,记作deg–(v)。
结点v的度为deg(v) = deg+(v) + deg–(v)。
约定:
无向图中的自环在其对应结点的度上增加2。
有向图中的自环在其对应结点的度上增加一个入度和一个出度。
定理 7.1 设图G具有结点集{v1,v2,…,vn}和m条边,则G中所有结点的度之和为G的边数的两倍,即
对于有向图,
推论 7.1 任何图G中,度为奇数的结点个数为偶数。
定义 7.12 若无向图的所有结点都具有同一个度d,则称该无向图G为d次正则图。
例如 无向完全图Kn是一个n – 1次正则图。
零图是0次正则图。
d次正则图的边数m = dn/2。
四、图的连通性
定义 7.13 图G中结点和边的序列
v1,e1,v2,e2,v3,…,vl,el,vl+1
称为结点v1到vl+1的一条长为l的路,常用结点的序列v1v2…vlvl+1来表示。其中ei(i = 1,2,…,l)以vi和vi+1为端点(有向图中,边ei为以vi为起点、以vi+1为终点的有向边)。
若v1 ≠ vl+1,则称路v1v2…vlvl+1为开路。在开路中,若所有边互不相同,则称该路为简单路,若所有结点互不相同(此时所有边也互不相同),则称该路为基本路或真路。
若v1 = vl+1,则称路v1v2…vlv1为回路。在回路中,若所有边互不相同,则称该路为简单回路,若v1,v2,…,vl各不相同(此时所有边也互不相同),则称该回路为基本回路或环。