斐波那契数与二分法的递归与非递归算法及其复杂度分析（转）

本文转自：斐波那契数与二分法的递归与非递归算法及其复杂度分析

1. 什么是斐波那契数？

这里我借用百度百科上的解释：斐波那契数，亦称之为斐波那契数列（意大利语： Successione di Fibonacci)，又称黄金分割数列、费波那西数列、费波拿契数、费氏数列，指的是这样一个数列：0、1、1、2、3、5、8、13、21、……在数学上，斐波纳契数列以如下被以递归的方法定义：F0=0，F1=1，Fn=Fn-1+Fn-2（n>=2，n∈N*），用文字来说，就是斐波那契数列列由 0 和 1 开始，之后的斐波那契数列系数就由之前的两数相加。特别指出：0不是第一项，而是第零项。

在这个斐波那契数列中的数字，就被称为斐波那契数。这个级数与大自然植物的关系极为密切。几乎所有花朵的花瓣数都来自这个级数中的一项数字：菠萝表皮方块形鳞苞形成两组旋向相反的螺线，它们的条数必须是这个级数中紧邻的两个数字（如左旋8行，右旋13行）；还有向日葵花盘……直到最近的1993年，人们才对这个古老而重要的级数给出真正满意的解释：此级数中任何相邻的两个数，次第相除，其比率都最为接近0.618034……这个值，它的极限就是所谓的"黄金分割数"。

2. 求第N个斐波那契数

求第N个斐波那契数比较简单可以直接套用公式n = 0,1 时，fib(n) = 1；n > =2 时，fib(n) = fib(n-2) + fib(n-1)在计算时有两种算法：递归和非递归。如下：

  //非递归算法
  long long fib1(size_t N) {
      long long a = 0, b = 1, c = 0;
      if (N < 2) {
          return N;
      }
      else {
          for (long long i = 2; i <= N; ++i) {
              c = a + b;
             a = b;
             b = c;
         }
     }
         return c;
 }
int main()
 {
     printf("%lld", fib1(10));
     getchar();
     return 0;
 }  //此算法最大的优点是不存在重复计算，故效率比递归算法快的多得多。

 //递归算法
 long long fib2(size_t N) {
     if (N < 2) 
         return N;
      return fib2(N - 1) + fib2(N - 2);
  }
 int main()
 {
      printf("%lld", fib2(10));
     getchar();
     return 0;
   }

递归可以使程序看起来比较简洁，但缺点是效率比较低，并且可能导致栈溢出，当需要计算的数稍大一点，就需要很长的计算时间，因此需要灵活使用递归。

3. 二分法查找

3.1 二分查找的非递归算法

  template  
  T* BinarySearch(T* array,int number,const T& data)  //data要查找的数，number查找范围长度，array要查找的数组
  {  
         assert(number>=0);  
         int left = 0;  
         int right = number-1;  
         while (right >= left)  
         {  
                int mid = (left&right) + ((left^right)>>1);  
               if (array[mid] > data)  
               {  
                      right = mid - 1;  
               }  
               else if (array[mid] < data)  
               {  
                      left = mid + 1;  
               }  
               else  
               {  
                      return (array + mid);  
               }  
        }  
        return NULL;  
 }  

3.2 二分查找递归算法

 template  
 T* BinarySearch(T* left,T* right,const T& data)  
 {  
        assert(left);  
        assert(right);  
        if (right >=left)  
        {  
               T* mid =left+(right-left)/2;  
               if (*mid == data)  
                      return mid;  
               else  
                      return *mid > data ? BinarySearch(left, mid - 1, data) : BinarySearch(mid + 1, right, data);  
        }  
        else  
        {  
               return NULL;  
        }  
 }  

4. 时间复杂度与空间复杂度

4.1. 时间复杂度：

一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数f(n)，进而分析f(n)随n的变化情况并确定T(n)的数量级。这里用"O"来表示数量级，给出算法的时间复杂度。
T(n)=O(f(n));
它表示随着问题规模的n的增大，算法的执行时间的增长率和f(n)的增长率相同，这称作算法的渐进时间复杂度，简称时间复杂度。而我们一般讨论的是最坏时间复杂度，这样做的原因是：最坏情况下的时间复杂度是算法在任何输入实例上运行时间的上界，分析最坏的情况以估算算法指向时间的一个上界。
时间复杂度的分析方法：
（1）时间复杂度就是函数中基本操作所执行的次数；
（2）一般默认的是最坏时间复杂度，即分析最坏情况下所能执行的次数；
（3）忽略掉常数项；
（4）关注运行时间的增长趋势，关注函数式中增长最快的表达式，忽略系数；
（5）计算时间复杂度是估算随着n的增长函数执行次数的增长趋势；
（6）递归算法的时间复杂度为：递归总次数 * 每次递归中基本操作所执行的次数；
常用的时间复杂度有以下七种，算法时间复杂度依次增加：O(1)常数型、O(log2 n)对数型、O(n)线性型、O(nlog2n)二维型、O(n^{2)平方型、O(n}3)立方型、O(2^n)指数型。

4.2. 空间复杂度：

算法的空间复杂度并不是计算实际占用的空间，而是计算整个算法的辅助空间单元的个数，与问题的规模没有关系。算法的空间复杂度S(n)定义为该算法所耗费空间的数量级。
S(n)=O(f(n)) 若算法执行时所需要的辅助空间相对于输入数据量n而言是一个常数，则称这个算法的辅助空间为O(1);
递归算法的空间复杂度：递归深度N*每次递归所要的辅助空间， 如果每次递归所需的辅助空间是常数，则递归的空间复杂度是 O(N)。

5. 斐波那契数的时间复杂度与空间复杂度分析

5.1 非递归算法时间复杂度分析

使用非递归算法求到第n个斐波那契数，是从第2个数开始，将前两个数相加求求后一个数，再将后一个数赋值给前一个数，再计算前两个数相加的结果。依次类推直到第n个数，用n-1个数和n-2个数相加求出结果，这样的好处是，我们只计算了n-1次就求出了结果，即时间复杂度为O(n)；我们以代码中测试数10为例详解求第十个数的过程。当N=10时，进入函数首先判断，然后走下面的分支开始计算

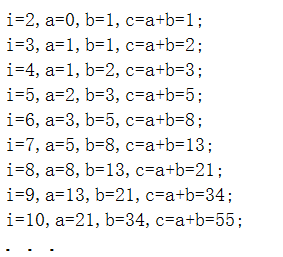
计算了N-1次，得出了结果所以时间复杂度是O（N）。

非递归算法空间复杂度分析
此函数内部最多时一共开辟了a, b, c, i四个变量空间复杂度是常数，即为O（1）。

5.2 递归算法时间复杂度分析

在递归算法中，求解fib2(n)，把它推到求解fib2(n-1)和fib2(n-2)。也就是说，为计算fib2(n)，必须先计算

fib2(n-1)和fib2(n-2)，而计算fib2(n-1)和fib2(n-2)，时按照表达式及计算法则，需先计算又必须先计算fib2(n-1)，而fib2(n-1)由fib2(n-2)和fib2(n-3)计算得来，而这之中的和fib2(n-2)由fib2(n-3)和fib2(n-4)计算得来…依次类推，表面上看不出有何复杂度，但是仔细分析可知，每一个计算fib2(n)的分支都会衍生出计算直至(1)和fib(0)，也就是说每个分支都要自己计算数本身到1的斐波那契数列，这样就增加了庞大且冗杂的运算量，还是以10 为例详细计算说明

图中数字代表第N个斐波那契数，图中没有全部将计算步骤画出来，但是已经足够说明问题，它的每一步计算都被分成计算前两个斐波那契数，以此类推。那么这就形成了一颗二叉树，虽然不是满二叉树，但是我们分析的是最坏时间复杂度，而且只要估算出来递归次数随N增长的趋势即可，故可以近似将它看成满二叉树，其中的节点数就是计算的次数，也就是复杂度，由公式：节点数=2^{h-1（h为树的高度）可得O（2}n）。

递归的时间复杂度是： 递归次数*每次递归中执行基本操作的次数，所以时间复杂度是： O(2^N)
递归算法空间复杂度分析：

递归最深的那一次所耗费的空间足以容纳它所有递归过程。递归产生的栈侦是要销毁的，所以空间也就释放了，要返回上一层栈侦继续计算+号后面的数，所以它所需要的空间不是一直累加起来的，之后产生的栈侦空间都小于递归最深的那一次所耗费的空间。

递归的深度*每次递归所需的辅助空间的个数 ，所以空间复杂度是：O(N)

6. 求二分法的时间复杂度和空间复杂度

6.1 非递归算法分析

分析：
假设最坏情况下，循环X次之后找到，则：2^x=n; x=logn(算法中如果没写，log默认底数为2)
循环的基本次数是log2 N，所以: 时间复杂度是O(logN);
由于辅助空间是常数级别的所以：空间复杂度是O(1);
6.2 递归算法复杂度分析

假设最坏情况下，循环X次之后找到，则：2^x=n; x=logn(算法中如果没写，log默认底数为2)
递归的次数和深度都是log2 N,每次所需要的辅助空间都是常数级别的：
时间复杂度:O(log2 N)；
空间复杂度：O(log2N )。
7. 扩展-----不用循环法和递归法求1+2+3+…+N（思考一种复杂度为O（1）的解法）

 class Temp
 {
 public:
     Temp(){
         ++N;
         Sum += N;
     }
     static void Reset(){
         N = 0;
         Sum = 0;
     }
     static int GetSum(){
         return Sum;
     }
 private:
     static int N;
     static int Sum;
 };
 int Temp::N = 0;
 int Temp::Sum = 0;
 int solution_Sum(int n){
     Temp::Reset();
     Temp *a = new Temp[n];
     delete[]a;
     a = 0;
     return Temp::GetSum();
 }
 int main(){
     cout << solution_Sum(100) << endl;
     getchar();
     return 0; 
 }