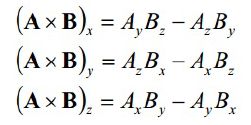PIXHAWK姿态控制整体框架及控制算法的深度解析

    上文写了PIXHAWK的位置控制算法，该文对其姿态控制进行深入解析。其中姿态控制主要看PX4的mc_att_control_main.cpp,其中姿态控制主要执行函数为MulticopterAttitudeControl::control_attitude(float dt)。姿态控制整体框架：角度环采用P控制,角速度采用PID控制（但含有很多先进PID的控制方法，文章会提到）。

        姿态控制首先要获得位置控制计算而得的期望旋转矩阵R_sp和当前的姿态旋转矩阵R。

代码：

R_sp.set(_v_att_sp.R_body);

R.set(_v_att.R);

其次便要获取两个旋转矩阵之间的误差角度，根据方向余弦矩阵求取角度误差，PX4中思想是先对齐Z轴（由于Z轴航向的响应相对横滚和俯仰较慢，故先对其Z轴），然后求取横滚和俯仰维度的角度误差，最后再对航向误差进行相对补偿，这样飞机的行驶路径相对最小，否则飞机在横滚、俯仰补偿的同时转动航向飞机转动行驶路线是个曲线，路径相对较长（个人对矩阵旋转的运动学理解）。英文解释：

/* try to move thrust vector shortest way, because yaw response is slower than roll/pitch */，

/* calculate rotation matrix after roll/pitch only rotation */。

        算法实现：首先对齐Z轴，求取横滚和俯仰的角度偏差：math::Vector<3> e_R = R.transposed() * (R_z % R_sp_z);

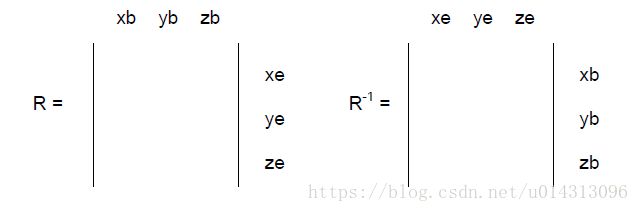
其中R_z % R_sp_z（向量叉乘）产生一个新的机体平面对应的法向量，R.transposed()为R的转置（旋转矩阵R见下图），航向z轴与新产生的法向量垂直，故此时求得的e_R（2）为0，只能求出对应的横滚、俯仰的角度偏差向量（不是实际的偏差值）R的转置与法向量相乘，是当前姿态矩阵在法向量上的投影，求取俩个姿态矩阵的误差。

接下来对实际的横滚，俯仰偏差值进行求解。根据叉乘、点乘公式，如下：

                                                                        

                                   

 

求取横滚、俯仰总旋转角度的正弦（旋转轴单位化）和余弦，代码：

float e_R_z_sin = e_R.length();

float e_R_z_cos = R_z * R_sp_z;

接下来PX4角度控制中依据角度偏差大小，对于响应方法进行了分类求取角度偏差。

        第一种：当横滚、俯仰总体角度未达到180度时（当然飞机默认横滚、俯仰最大期望角度45度，一般不会达到第二种情况），依旧正切求取横滚、俯仰总体偏差角度，代码:

float e_R_z_angle = atan2f(e_R_z_sin, e_R_z_cos);

然后对之前求取的e_R进行归一化，分别求取横滚、俯仰对应的角度偏差，代码：

 e_R_z_axis = e_R / e_R_z_sin;

e_R = e_R_z_axis * e_R_z_angle;

最后依据求得的横滚、俯仰的角度偏差对旋转矩阵进行旋转，得到新的旋转矩阵R_rp，R_rp与原期望矩阵R_sp有相同的Z轴，然后计算航向角度偏差，原文注释讲解：/* R_rp and R_sp has the same Z axis, calculate yaw error */。在求取R_sp时，采用罗德里格旋转公式，用等效旋转单位矢量e_R_z_axis构造反对称矩阵math::Matrix<3, 3> e_R_cp（在秦永元的《惯性导航》第二版书p252中有讲解）和旋转角度来求取对应的旋转矩阵R_rp。书中描写如下：

mahony的论文中也有提到，小的旋转可以由反对称矩阵来表示，文章截图如下：

代码实现如下：

math::Matrix<3, 3> e_R_cp;
e_R_cp.zero();
e_R_cp(0, 1) = -e_R_z_axis(2);
e_R_cp(0, 2) = e_R_z_axis(1);
e_R_cp(1, 0) = e_R_z_axis(2);
e_R_cp(1, 2) = -e_R_z_axis(0);
e_R_cp(2, 0) = -e_R_z_axis(1);

e_R_cp(2, 1) = e_R_z_axis(0);


/* rotation matrix for roll/pitch only rotation */

R_rp = R * (_I + e_R_cp * e_R_z_sin + e_R_cp * e_R_cp * (1.0f - e_R_z_cos));

最后依据对其Z轴的R_rp和R_sp求取航向角偏差，代码：

e_R(2) = atan2f((R_rp_x % R_sp_x) * R_sp_z, R_rp_x * R_sp_x) * yaw_w;

这里R_rp_x * R_sp_x相当于求取机头旋转偏差的余弦，R_rp_x % R_sp_x相当于求取机头旋转偏差的正弦，但仍是一向量，点乘R_sp_z后将该向量分解到z轴（求解思想与e_R = R.transposed() * (R_z % R_sp_z)一致，点乘可以互换位置(R_rp_x % R_sp_x) * R_sp_z的结果恰好是R_rp_x % R_sp_x的长度sin，R_rp_x * R_sp_x为cos），yaw_w是一个与横滚、俯仰角旋转有关的衰减系数，其目的是先进行横滚、俯仰角的旋转，其代码：

float yaw_w = R_sp(2, 2) * R_sp(2, 2);

旋转矩阵可见下式：

        当横滚、俯仰总体角度偏差较大时>90度，采用第二种求取角度偏差的方法，不考虑旋转顺序，这里采用四元数求取角度偏差（这里是因为ZYX旋转矩阵在横滚角90时存在奇点），原文注释：

/* for large thrust vector rotations use another rotation method:
* calculate angle and axis for R -> R_sp rotation directly */

采用四元数一次旋转到位。

PX4中由四元数求取角度偏差的方法：首先求取由当前旋转矩阵旋转到目标旋转矩阵（R -> R_sp）的过渡矩阵，从而将其转换成四元数，代码：q.from_dcm(R.transposed() * R_sp);（这里R的逆=R的转置，对应旋转在机体系，见下图）

其中四元数可以由三角式来表示：

求取四元数的虚部，归一化后根据三角表达式依据正切求取旋转角度，代码如下：

                e_R_d = q.imag();
                e_R_d.normalize();

                e_R_d *= 2.0f * atan2f(e_R_d.length(), q(0));

最后将第一种算法求得的结果与该种算法的结果互补一下，代码：

 

               e_R = e_R * (1.0f - direct_w) + e_R_d * direct_w;

其中互补系数与横滚、俯仰角度有关：direct_w = e_R_z_cos * e_R_z_cos * yaw_w;(当两Z轴夹角为0时, yaw_w为1; 两轴夹角为90°, 由于欧拉角的奇异点, yaw与pitch重合, 无需控制yaw, 此时yaw_w为0，计算e_R的后半部分对于航向误差照顾的多一些)。

        求取到角度偏差后，便需要将其转化成角速度控制输入（P控制）即角速度设定值，代码：

       /* calculate angular rates setpoint */

        _rates_sp = _params.att_p.emult(e_R);

其中emult代表乘_params.att_p是角度环的一个比例控制参数。接下来对期望角速度进行限幅，由于航向响应较慢，故对航向加入前馈控制（这与前面提到的先进行横滚、俯仰的旋转不矛盾，最后的偏航响应也要跟上），代码：

/* limit rates */
for (int i = 0; i < 3; i++) {
_rates_sp(i) = math::constrain(_rates_sp(i), -_params.mc_rate_max(i), _params.mc_rate_max(i));
}
/* feed forward yaw setpoint rate */

_rates_sp(2) += _v_att_sp.yaw_sp_move_rate * yaw_w * _params.yaw_ff;

接着依据PID求取角速度环的输出：

_att_control = _params.rate_p.emult(rates_err) + _params.rate_d.emult(_rates_prev - rates) / dt + _rates_int + _params.rate_ff.emult(_rates_sp - _rates_sp_prev) / dt;

分别对应误差比例、和对传感器数据的微分、误差积分还有期望值的微分对应的前馈。

对于积分，PX4中进行了抗积分饱和的操作，代码：

/* update integral only if not saturated on low limit and if motor commands are not saturated */

if (_thrust_sp > MIN_TAKEOFF_THRUST && !_motor_limits.lower_limit && !_motor_limits.upper_limit ) {
    for (int i = 0; i < 3; i++) {
        if (fabsf(_att_control(i)) < _thrust_sp) {
            float rate_i = _rates_int(i) + _params.rate_i(i) * rates_err(i) * dt;
            if (isfinite(rate_i) && rate_i > -RATES_I_LIMIT && rate_i < RATES_I_LIMIT &&
               _att_control(i) > -RATES_I_LIMIT && _att_control(i) < RATES_I_LIMIT) {
                _rates_int(i) = rate_i;
            }
        }
    }
}

其中_thrust_sp > MIN_TAKEOFF_THRUST指须离地后采用积分；!_motor_limits.lower_limit && !_motor_limits.upper_limit 指计算得到的对应电机的输入值既未小于下限，也未大于上限才可以进行积分；if (fabsf(_att_control(i)) < _thrust_sp)为分通道角速度环计算输出值小于总体推力设置值才进行积分（角速度的输出对应力的量纲？后面需要思考），这三条限制为积分分离。（!_motor_limits.lower_limit && !_motor_limits.upper_limit 会在下一集PX4_mixer通道分配的深度解析中进行讲解）

其中if (isfinite(rate_i) && rate_i > -RATES_I_LIMIT && rate_i < RATES_I_LIMIT &&
    _att_control(i) > -RATES_I_LIMIT && _att_control(i) < RATES_I_LIMIT) 为抗积分饱和，即进行积分限幅，输出值达到限幅时也进行积分限幅，可谓双重抗积分饱和，这也是相对底层算法的精细之处。下集将进行PX4_mixer通道分配的深度解析，也谓输入到电机的最底层算法啦，涉及到PX4通道分配中的一个比例钳位的思想。

    好多月后，在网上发现一文（2016年的）对于这部分，写的很不错，网址：http://nutshellking.com/articles/xue-xi-zong-jie/Pixhawk_attitude_control/#1

      欢迎加入欣飞鸽总动员一起交流讨论，qq群聊号码：879466897

      更多飞控精彩好文干货，请关注微信公众号：欣飞鸽。

       开心飞翔，灵动如鸽，愿与无人机爱好者共创一片蓝天梦！