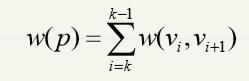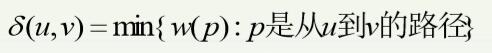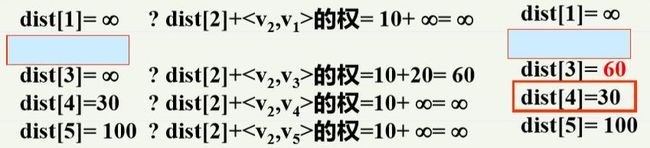数据结构:图(三) 图的应用
这篇文章讲一下图的一些应用。
一、最小连通代价问题
二、最短路径问题
三、有向图在工程中的应用(AOV网络、AOE网络)
一、最小连通代价问题
无向连通图的生成树有很多,如果图的边具有权值,那么各个生成树的边的权值之和大小就不同。在所有生成树中,权值之和最小的一棵成为最小生成树。
1.最小生成树:假设图是一个加权连通图,具有最小权值之和的生成树称为最小代价生成树。Minimum Cost Spanning Tree (MST)
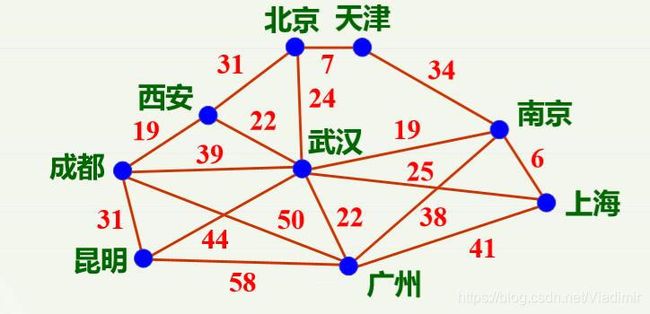
举一个例子:假设有一个网络,用以表示n个城市之间假设通信线路,边上的权值代表架设通信线路的成本。如何架设才能使线路架设成本达到最小?
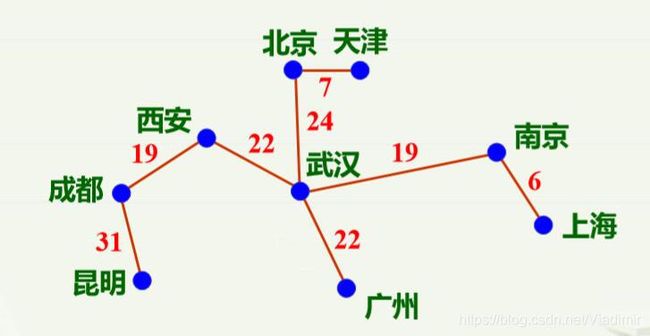
这个问题的答案:
2.MST性质:假设 G=(V,E) 是加权连通图,U是V的非空子集, 若(u0, v0)是一条最小权值的边,其中u0∈U,v0∈V-U;则: (u0, v0)必在最小生成树上。 (这里给大家说一下,所谓最小权值的边,我认为是与u0相连的所有带权值边中权值最小的边,而不是所有带权值边中权值最小的边(也可能理解的不对,有不对的地方还请大家批评指正))
3.最小生成树的构造方法
有多种算法,最常用的是以下两种:Kruskal(克鲁斯卡尔)算法——边归并 、Prim(普里姆)算法 ——顶点归并。
这两种方法都是采用的贪心策略,都是基于MST性质的。
贪心准则:选两个顶点不在同一连通分量上的边中权值最小的。
(1)克鲁斯卡尔(Kruskal)方法:
设 N= { V , E}是有n 个顶点的连通网,
步骤:
①首先构造一个只有n个顶点但没有边的非连通图T={V,∅},图中每个顶点自成一个连通分量;
②在边集E中选择具有最小权值的边,若该边的两个顶点落在T中不同的连通分量上,则将此边加入到生成树的边集合T 中;否则将此边舍去,重新选择一条权值最小的边;
③如此重复下去,直到所有顶点在同一个连通分量上为止。 此时的T即为所求(最小生成树)。
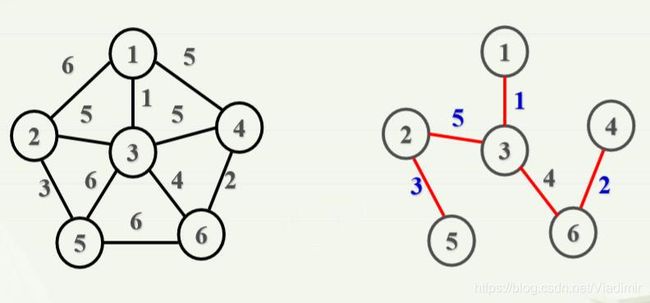
举例:
右图中边的权值由小到大代表该边被选择的顺序(如权值为2的边,代表该边是第二个被选择的边)。
(2)普利姆(Prim)方法:
设:N =(V , E)是个连通网, 另设U为最小生成树的顶点集,TE为最小生成树的边集。
步骤:
①初始状态:令U={u0},u0∈V,TE={},T={V,TE};
②在所有u∈U,v∈V-U的边(u,v)中找一条权值最小的(u',v'),(u',v')并入TE,即TE=TE∪{(u′,v′)},v′并入U,即U=U∪{v′};
③ 重复第二步,直到U=V为止。此时TE中必有n-1条边, T=(U,TE)就是最小生成树。
举例:
二、最短路径问题
在现实中,有时要从甲地到乙地,有两种型录的方案:
其一:为了减少麻烦,选择中转次数最少的路线;
其二:为了节省时间,选择距离最短的路线;
第一种方法,可以利用图的广度优先遍历方法,将从甲地到乙地的所有路线找出来,然后找一条中转次数最少的路线;第二种方法,就是这篇文章要讨论的最短路径问题,根据图中各边的权值选择路径。
给定一个带权重的图G=(V,E),边的权重函数为w:E->R,则一条路径p=v1 →v2 →… →vk的权重为该路径上每条边的权重之和:
1.最短路径:无论是有向图还是无向图,从任意定点u到v的最短路径是从所有u到v的路径中权重最小的路径。最短路径权重定 义为:
2.最短路径问题:
(1)单源单点最短路径问题:人们最容易想到也是现实生活中最常见的问题
直观感觉上,寻找单源单点最短路径的时间复杂性将大大超过边的数目。时间复杂性与一对顶点之间的路径的条数成正比,那么一对顶点之间,最坏情况下至少是(n-2)!,至多是(n-1)!,n=|V|,即O(n!)。因此,最坏时间复杂性是巨大的。
对于一般性的一对顶点(单源单点)之间的最短路径问题,目前还没有找到更好的办法。
(2)单源多点最短路径问题:Dijkstra(迪杰斯特拉)算法
尽管比较糟糕,但是人们发现,在找一对顶点之间的最短路径时,已经考察了源点到任意顶点的所有路径,因此,可以一次性地找出源点到所有顶点的最短路径,这样平摊下,花费在一对顶点之间的最短路径上的成本会大大降低。求一个顶点到其他所有顶点的最短路径问题可以使用贪心策略,贪心+摊销,从而使得最短路径的搜索成本大大下降。
Dijkstra算法:
1)问题描述:设一有向图G=(V, E),已知各边的权值,以某指定点v0为源点,求从v0到图的其余各点的最短路径。限定各边上的权值大于或等于0。
2) Dijkstra 算法的基本思想
贪心策略:从源点向外延伸,越短的路径(终点)越早被求出。(大家可以将其想象成洪水泛滥,从一个村庄淹没到另一个村庄,洪水当然会“走”距离最短的路径)
即:找出目前离源点最近的顶点(它和源点构成了一条新 的最短路径,这条路径应该在未求出的路径中最短。)
于是,第一条最短路径是,从源点出发,不经过任何顶点可达的所有路径中最短的那条。
按照Dijkstra的思想,第二条肯定比第一条要长,但应该是 从源点可达的路径中最短的那条。有两种可能:
①从源点直达
②经过其他顶点,此时要经过只能经过第一条(的顶点)
3)Dijkstra 算法 :设v0是源点,S={v1,…,vk}是已经求得最短路径的顶点集合, V-S就是还未求出最短路径的顶点集合。一个顶点vi属于 S当且 仅当从源点v0到vi的最短路径已经求出。
引入一个辅助数组dist。它的每一个分量dist[i]记录着源点v0 到vi的当前最短路径长度。
①初始化:
dist的初始状态:对每个顶点有:
·若从v0到顶点vi有边, 则dist[i]为该边的权值;
·若从v0到顶点vi无边, 则dist[i]为无穷。
②求一条最短路径:
(应用贪心准则选择求出每一条最短路径)
即在未求出最短路径的顶点中选取离源点距离最近的顶点。在V-S中,选取具有最短当前路径的顶点vk,满足:dist[k]=min{ dist[i] | vi ∈V-S } ,S<-S∪{vk};
③修正:对所有未求出最短路径且又与vk邻接的顶点vj ∈V-S 按下式修正(新最短路径的出现是否使各个顶点的当前路径变 短),即:
dist[j]=min{ dist[j],dist[k]+w(k,j) }
④重复②③,直到S=V。到这里,所有顶点的最短路径都已经求出。
注意:在记录路径长度的同时, 还应该记录路径轨迹,即哪条 路径最短。
(上面这些对于迪杰特斯拉算法的描述,有些地方我自己都读不明白,大家粗略的看一下即可,主要看一下我下面展示的这个例子)
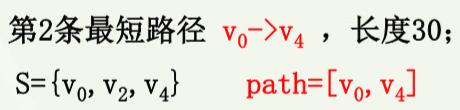
4)举例:
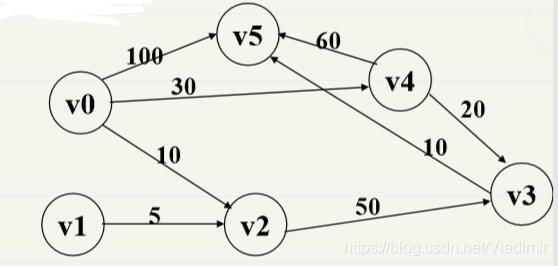
求v0到其余各顶点的最短路径。
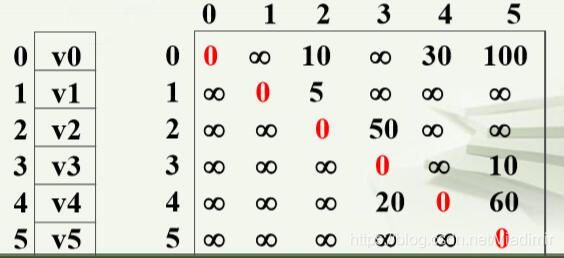
①存储结构:加权邻接矩阵
②初始化:
(上面那个红框应该是框错了)
path[3]=[v0,v2,v3]
迪杰特斯拉算法,按照我的理解,其实就一句话,路径经过的所有顶点向其他未被包括的所有顶点“发出连接请求”,从中选一个权值增加最小的,加入当前最短路径顶点集合中。
(3)多源多点最短路径问题:Floyd(弗洛伊德)算法
1)问题:对于有向加权图G,求每一对顶点之间的最短路径。
2)方法:
①方法1:调用上面的迪杰特斯拉算法,以每个顶点作为一次源点。
②方法2:Floyd算法(这个算法我们不考,老师也没讲,这里我就不说了,有兴趣的童鞋可以问一下度娘)
三、有向图在工程中的应用
1.先说两个概念。
工程(project):有时又称为系统,一般指一项大的或复杂的任务。
活动(activity):复杂工程一般要分解为许多子工程,每个子工程称为活动。
2.工程:
(1)AOV网络:各个子工程(活动)如何施工,以保证工程能够完成。(哪个活动先开始,那个活动后开始,因为某些活动可能以其他活动的完成为前提,这是调度问题)
(2)AOE网络:工程何时能完工,各个活动的完成时间决定工程完成的总时间。(如何估算工程的工期,使工期最短,这是进度、工期问题)
3.AOV网络
(1)AOV网络:用顶点表示工程的活动,有向边表示活动之间 的优先关系( Activity On Vertex )的有向图。
(2)前驱、后继:在AOV网络中,若从顶点Vi到Vj有一条有向路 径,则称Vi是Vj的前驱,Vj是Vi的后继;若
前驱后继关系表示一个活动是另一个活动的先决条件,即前驱活动完成,后继活动才可以开始。
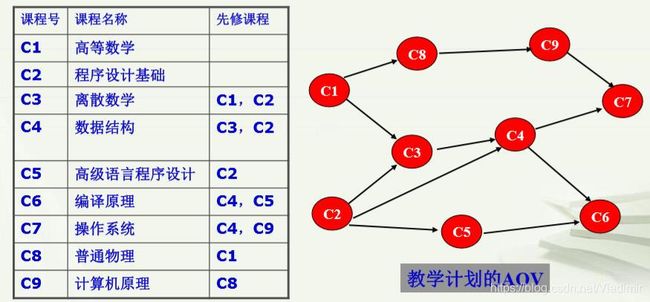
(3)举一个例子:
计算机专业学生必须完成一系列规定的基础课和专业课 才能毕业,这就是一个工程。学习一门课程就是一个活动。先 学哪些课,后学哪些课是有要求的,即活动之间有优先关系。
(4)拓扑序列:对于有向图,其顶点V1,V2,...Vn的一种排列,如果 满足:Vi到Vj有一条有向路径,则Vi排在Vj前面。则称顶点是 拓扑有序的,亦称为顶点的一个拓扑序列。
如果顶点集合(工程的活动)能排为拓扑序列,则说明 工程就得到了一个合理的施工调度方案。
拓扑排序(分类):得到AOV网络顶点的一个拓扑序列的过程。
总的来说:对于一个工程,进行任务分解,得到各个子工程(活动), 确定它们之间的优先关系,然后就可以构建出AOV网络。如果 能得到AOV网络的顶点的一个拓扑序列,就得到了工程的一个 活动(施工)调度方案。
(5)要特别注意一点,AOV网络中不能有环,如果有环的话,通俗点讲,会进入一个无穷的循环。
判断AOV有没有环的方法:看能否找到AOV网络顶点的一个拓扑排列(拓扑序), 若所有顶点能排成一个拓扑序列,则不存在环,否则, 有环。
(6)进行拓扑排序的方法:重复选取入度为0的顶点输出;
假设AOV网络中有n个顶点(活动、子工程),拓扑排序的步骤:
1)在AOV网络中选一个没有直接前驱的顶点(入度为0), 并输出之; 如果有多个,可以任意选一个;
2)从AOV中删去该顶点及关联的边(即凡是以该顶点为前 提条件的,都没有了,邻接顶点的入度减1) ;
3)重复(1)、(2)步, 直到:
①全部定点均已输出(得到拓扑有序序列);
②AOV中已没有入度为0的顶点(AOV中剩余的顶点构成 有向环)
4.AOE网络
(1)事件(Event):一些活动完成后产生的结果或状态。
(2)AOE网络:用顶点表示事件,有向边表示活动,有向边上的 权值表示活动的持续时间,这样的有向图称为AOE网络 ( Activity On Edge ) 。
(3)一些概念:
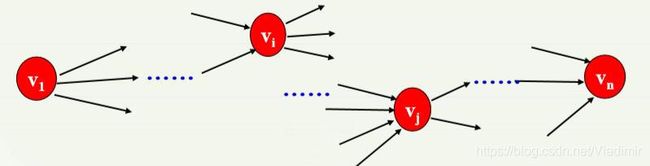
1)源点:在AOE中,只有一个入度为0的顶点(起始事件);
2)汇点: 在AOE中,只有一个出度为0的顶点(结束事件);
3)活动与事件的关系:事件发生后,从此事件出发的活动就 可以开始了;进入(影响)事件的活动都完成该事件就发生;
4)AOE表示的工程:源点(开工)事件发生后,一些活动开始, 一些活动的结束,又导致发生新事件,新事件发生又有活动开 始......,最后,一些活动完成,产生汇点(竣工)事件;
5)工程的工期:源点到汇点所有有向路径中,权值之和最长的路 径的长度。这条路径长度最长的路径就叫做关键路径(Critical Path);
6)事件 Vi 的最早发生时间Ve(Vi)=从源点V1到事件Vi的所有有向路径中,权值之和最长的路径的长度;
7)事件 Vi 的最迟发生时间Vl(Vi)=在保证汇点Vn 在Ve[Vn] 时刻完成的前提下,事件Vi的允许的最迟开始时间 =工程的工期-从事件Vi到汇点所有有向路径中权值之和最长的路径的长度;
8)活动的最早开始时间Ae(ek)= 若 ek = < Vi,Vj>,该活动的最早开 始时间为该活动起始事件Vi的最早发生时间 Ve(Vi);
9)活动的最晚开始时间Al(ek)= 若 ek = < Vi,Vj>,该活动的最迟允 许开始时间为该活动的终止事件Vj的最晚发生时间 Vl(Vj)- ek持 续时间;
10)时间余量(松弛时间 slack time)= Al(ek)-Ae(ek)
11)关键活动:时间余量为0,即Ae(ek)=Al(ek)
AOE网络的主要问题,就是求出关键路径。
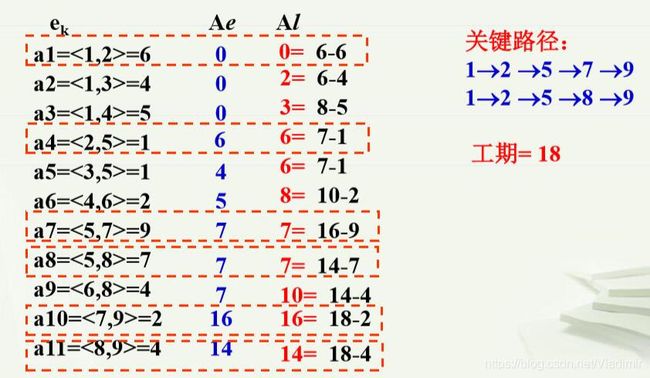
(4)关键路径求法
1)求出各个事件的最早发生时间 Ve(Vj) ,然后:
2)求出各个事件的最晚发生时间 Vl(Vi) ,汇点(结束事件)的最晚发生时间等于它的最早发生时间 Vl(Vn)=Ve(Vn),然后:
3)求出各个活动的最早开始时间Ae(ek) ,若 ek = < Vi,Vj>,则Ae(ek)=Ve(Vi);
4)求出各个活动的最晚开始时间Al(ek) ,若 ek = < Vi,Vj>,则Al(ek)=Vl(Vj)-
5)找出关键活动 ;
6)求出关键路径、工期 ;
7)结论(缩短工期的方法) :工程管理策略。
举个例子:
总结一下 :
1.对于一个工程,可以利用AOV网络分析工程在分解时是否合理(各个子工程间有否冲突);得到工程施工的调度顺序。
2.、对于一个工程,在AOV的基础上,可以利用AOE网 络分析工程的关键子工程(抓主要活动—关键活动),计算 (预测)工程的工期。
3.、在不改变关键路径的前提下,提高关键活动的效率(即缩短关键活动所花费的时间),可以缩短工期。