12.排序(下)
12.排序(下):如何用快排思想在O(n)内查找第K大元素?
markdown文件已上传至github
冒泡排序、选择排序、插入排序的时间复杂度都是O(n^2),适合小规模数据的排序。这一节介绍两种时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)的排序算法,归并排序和快速排序。这两种排序算法适合大规模的数据排序,更常用,它们都用了分治的思想,可以借鉴这个思想来解决排序的问题,比如:如何在 O ( n ) O(n) O(n)的时间复杂度内查找一个无序数组中第K大元素?
1.归并排序的原理
核心思想:先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排序好的两部分合并在一起,这样整个数组就有序了。

归并排序使用的是**“分治思想”**,即分而治之,将一个大问题分解成小的子问题来解决,小的问题解决了,大问题也就解决了。分治一般用递归来实现,分治是一种解决问题的处理思想,递归是一种编程技巧。
第十节讲过:写递归的技巧是:先分析得出递推公式,然后找到终止条件,最后将递推公式翻译成递归代码。
归并排序的递推公式:
m e r g e _ s o r t ( p . . . r ) = m e r g e ( m e r g e _ s o r t ( p . . . q ) , m e r g e _ s o r t ( q + 1... r ) ) 终 止 条 件 : p > = r 不 用 继 续 分 解 merge\_sort(p...r)=merge(merge\_sort(p...q),merge\_sort(q+1...r)) \\终止条件: p >= r 不用继续分解 merge_sort(p...r)=merge(merge_sort(p...q),merge_sort(q+1...r))终止条件:p>=r不用继续分解
merge_sort(p…r) 表示,给下标从 p 到 r 之间的数组排序。我们将这个排序问题转化为了两个子问题,merge_sort(p…q) 和 merge_sort(q+1…r),其中下标 q 等于 p 和 r 的中间位置,也就是 (p+r)/2。当下标从 p 到 q 和从 q+1 到 r 这两个子数组都排好序之后,我们再将两个有序的子数组合并在一起,这样下标从 p 到 r 之间的数据就也排好序了。
伪代码:
// 归并排序算法, A是数组,n表示数组大小
merge_sort(A, n) {
merge_sort_c(A, 0, n-1)
}
// 递归调用函数
merge_sort_c(A, p, r) {
// 递归终止条件
if p >= r then return
// 取p到r之间的中间位置q
q = (p+r) / 2
// 分治递归
merge_sort_c(A, p, q)
merge_sort_c(A, q+1, r)
// 将A[p...q]和A[q+1...r]合并为A[p...r]
merge(A[p...r], A[p...q], A[q+1...r])
}
merge(A[p…r], A[p…q], A[q+1…r]) 这个函数的作用就是,将已经有序的 A[p…q]和 A[q+1…r]合并成一个有序的数组,并且放入 A[p…r]。
具体:如图所示,我们申请一个临时数组 tmp,大小与 A[p…r]相同。我们用两个游标 i 和 j,分别指向 A[p…q]和 A[q+1…r]的第一个元素。比较这两个元素 A[i]和 A[j],如果 A[i]<=A[j],我们就把 A[i]放入到临时数组 tmp,并且 i 后移一位,否则将 A[j]放入到数组 tmp,j 后移一位。

伪代码:
merge(A[p...r], A[p...q], A[q+1...r]) {
var i := p,j := q+1,k := 0 // 初始化变量i, j, k
var tmp := new array[0...r-p] // 申请一个大小跟A[p...r]一样的临时数组
while i<=q AND j<=r do {
if A[i] <= A[j] {
tmp[k++] = A[i++] // i++等于i:=i+1
} else {
tmp[k++] = A[j++]
}
}
// 判断哪个子数组中有剩余的数据
var start := i,end := q
if j<=r then start := j, end:=r
// 将剩余的数据拷贝到临时数组tmp
while start <= end do {
tmp[k++] = A[start++]
}
// 将tmp中的数组拷贝回A[p...r]
for i:=0 to r-p do {
A[p+i] = tmp[i]
}
}
归并排序性能分析:
1.归并排序是稳定的排序算法。(当有相同大小的值时,合并时将左数组的值先放入temp数组)
2.时间复杂度分析
定义求解问题 a 的时间是 T(a),求解问题 b、c 的时间分别是 T(b) 和 T( c),那我们就可以得到这样的递推关系式:
T ( a ) = T ( b ) + T ( c ) + K T(a) = T(b) + T(c) + K T(a)=T(b)+T(c)+K
其中 K 等于将两个子问题 b、c 的结果合并成问题 a 的结果所消耗的时间。
不仅递归求解的问题可以写成递推公式,递归代码的时间复杂度也可以写成递推公式。
我们假设对 n 个元素进行归并排序需要的时间是 T(n),那分解成两个子数组排序的时间都是 T(n/2)。我们知道,merge() 函数合并两个有序子数组的时间复杂度是 O(n)。所以,套用前面的公式,归并排序的时间复杂度的计算公式就是:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲& T(1) = C; \s…
具体计算过程:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲T(n) &= 2*T(n/2…
当 T ( n / 2 k ) = T ( 1 ) T(n/2^k)=T(1) T(n/2k)=T(1)时,即 n / 2 k = 1 n/2^k=1 n/2k=1时,得到 k = l o g 2 n k=log_2n k=log2n ,将k带入上面的公式,得到 T ( n ) = C n + n l o g 2 n T(n) = Cn +nlog_2n T(n)=Cn+nlog2n,用大O表示法表示,即T(n)=O(nlogn),所以归并排序的时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)。
从我们的原理分析和伪代码可以看出,归并排序的执行效率与要排序的原始数组的有序程度无关,所以其时间复杂度是非常稳定的,不管是**最好情况、最坏情况,还是平均情况,时间复杂度都是 O(nlogn)。****
3.归并排序的空间复杂度
递归代码的空间复杂度并不能像时间复杂度那样累加。刚刚我们忘记了最重要的一点,那就是,尽管每次合并操作都需要申请额外的内存空间,但在合并完成之后,临时开辟的内存空间就被释放掉了。在任意时刻,CPU 只会有一个函数在执行,也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小,所以空间复杂度是 O(n)。快速排序的原理
2.快速排序的原理
如果要排序数组中下标从 p 到 r 之间的一组数据,我们选择 p 到 r 之间的任意一个数据作为 pivot(分区点)。我们遍历 p 到 r 之间的数据,将小于 pivot 的放到左边,将大于 pivot 的放到右边,将 pivot 放到中间。经过这一步骤之后,数组 p 到 r 之间的数据就被分成了三个部分,前面 p 到 q-1 之间都是小于 pivot 的,中间是 pivot,后面的 q+1 到 r 之间是大于 pivot 的。
用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据,直到区间缩小为 1,就说明所有的数据都有序了。
递推公式:
q u i c k _ s o r t ( p … r ) = q u i c k _ s o r t ( p … q − 1 ) + q u i c k _ s o r t ( q + 1 … r ) 终 止 条 件 : p > = r quick\_sort(p…r) = quick\_sort(p…q-1) + quick\_sort(q+1… r)\\终止条件:p >= r quick_sort(p…r)=quick_sort(p…q−1)+quick_sort(q+1…r)终止条件:p>=r
伪代码:
// 快速排序,A是数组,n表示数组的大小
quick_sort(A, n) {
quick_sort_c(A, 0, n-1)
}
// 快速排序递归函数,p,r为下标
quick_sort_c(A, p, r) {
if p >= r then return
q = partition(A, p, r) // 获取分区点
quick_sort_c(A, p, q-1)
quick_sort_c(A, q+1, r)
}
归并排序中有一个 merge() 合并函数,我们这里有一个 partition() 分区函数。partition() 分区函数实际上我们前面已经讲过了,就是随机选择一个元素作为 pivot(一般情况下,可以选择 p 到 r 区间的最后一个元素),然后对 A[p…r]分区,函数返回 pivot 的下标。
partition() 分区函数:
partition(A, p, r) {
pivot := A[r]
i := p
for j := p to r-1 do {
if A[j] < pivot {
swap A[i] with A[j]
i := i+1
}
}
swap A[i] with A[r]
return i
快速排序和归并排序的区别:
归并排序的处理过程是由下到上的,先处理子问题,然后再合并。而快排正好相反,它的处理过程是由上到下的,先分区,然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法,但是它是非原地排序算法。我们前面讲过,归并之所以是非原地排序算法,主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数,可以实现原地排序,解决了归并排序占用太多内存的问题。
快速排序性能分析
1.快速排序是一种原地排序算法。
2.快速排序是一种不稳定的排序算法。(比如6,8,7,6,3,5,9,4,经过第一次分区后,两个6的先后顺序会改变)
3.快速排序的时间复杂度为 O ( n l o g n ) O(nlog n) O(nlogn)。在原有数据有序的情况下退化为 O ( n 2 ) O(n^2) O(n2)。
3.解答开篇
如何在 O ( n ) O(n) O(n)的时间复杂度内查找一个无序数组中第K大元素?
选择数组区间 A[0…n-1]的最后一个元素 A[n-1]作为 pivot,对数组 A[0…n-1]原地分区,这样数组就分成了三部分,A[0…p-1]、A[p]、A[p+1…n-1]。如果 p+1=K,那 A[p]就是要求解的元素;如果 K>p+1, 说明第 K 大元素出现在 A[p+1…n-1]区间,我们再按照上面的思路递归地在 A[p+1…n-1]这个区间内查找。同理,如果 K 第一次分区查找,我们需要对大小为 n 的数组执行分区操作,需要遍历 n 个元素。第二次分区查找,我们只需要对大小为 n/2 的数组执行分区操作,需要遍历 n/2 个元素。依次类推,分区遍历元素的个数分别为、n/2、n/4、n/8、n/16.……直到区间缩小为 1。如果我们把每次分区遍历的元素个数加起来,就是:n+n/2+n/4+n/8+…+1。这是一个等比数列求和,最后的和等于 2n-1。所以,上述解决思路的时间复杂度就为 O(n)。 现在你有 10 个接口访问日志文件,每个日志文件大小约 300MB,每个文件里的日志都是按照时间戳从小到大排序的。你希望将这 10 个较小的日志文件,合并为 1 个日志文件,合并之后的日志仍然按照时间戳从小到大排列。如果处理上述排序任务的机器内存只有 1GB,你有什么好的解决思路,能“快速”地将这 10 个日志文件合并吗? 法1:每次从各个文件中取一条数据,在内存中根据数据时间戳构建一个最小堆,然后每次把最小值给写入新文件,同时将最小值来自的那个文件再出来一个数据,加入到最小堆中。这个空间复杂度为常数,但没能很好利用1g内存,而且磁盘单个读取比较慢,所以考虑每次读取一批数据,没了再从磁盘中取,时间复杂度还是一样O(n)。 法2:先取得十个文件时间戳的最小值数组的最小值a,和最大值数组的最大值b。然后取mid=(a+b)/2,然后把每个文件按照mid分割,取所有前面部分之和,如果小于1g就可以读入内存快排生成中间文件,否则继续取时间戳的中间值分割文件,直到区间内文件之和小于1g。同理对所有区间都做同样处理。最终把生成的中间文件按照分割的时间区间的次序直接连起来即可。 这个是我学习王争老师的《数据结构与算法之美》所做的笔记,王争老师是前谷歌工程师,该课程截止到目前已有87244人付费学习,质量不用多说。 截取了课程部分目录,课程结合实际应用场景,从概念开始层层剖析,由浅入深进行讲解。本人之前也学过许多数据结构与算法的课程,唯独王争老师的课给我一种茅塞顿开的感觉,强烈推荐大家购买学习。课程二维码我已放置在下方,大家想买的话可以扫码购买。 本人做的笔记并不全面,推荐大家扫码购买课程进行学习,而且课程非常便宜,学完后必有很大提高。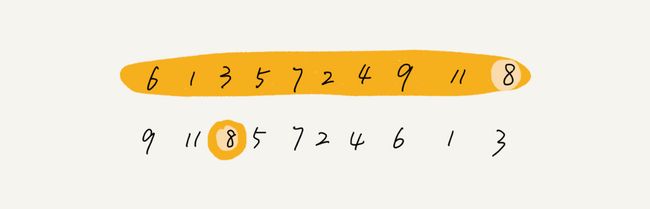
4.课后思考
5.参考
![]()
![]()