【洛谷P4201】设计路线【树形dp】

题目大意：

题目链接：https://www.luogu.org/problemnew/show/P4201
在一个$n$个点$m$条边的森林中选择若干路径，同时必须保证每个点最多在一条被选路径上。求所有点到点1的未选路径之和的最小值以及方案数。

---

思路：

思路来自$Sooke$大佬 https://www.luogu.org/blog/Sooke/solution-p4201
显然这个森林为一棵树的时候才能满足所有点都可以到达点1。
所以若$m̸=n-1$的话直接输出两个$-1$即可。
剩下的都是一棵树的情况。

---

先考虑如何求第一问的最小值。
因为一个点为了满足最多在一条被选路径上的要求，所以最多有2条与这个点相连的边被选择。三种情况如下图：

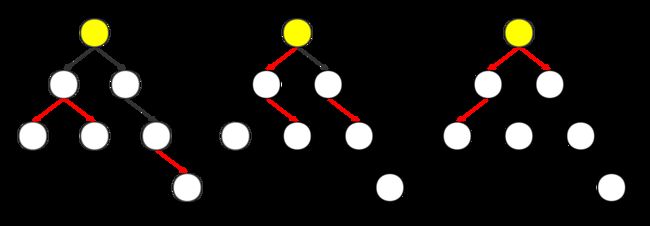
这三种情况就分别为没有与这个点相邻的边，有1个和有2个。
设$f[x][i]$表示在以$x$为根的子树内，有不多于$i(0\le x\le 2)$条选择的边与$x$相邻的未选路径之和的最小值。那么先分开成3种情况讨论，然后再取一个$min$即可。
$$\{\begin{array}{c}f[x][2]=min(max(f[x][2],f[y][2]+1),max(f[x][1],f[y][1]))\\ f[x][1]=min(max(f[x][1],f[y][2]+1),max(f[x][0],f[y][1]))\\ f[x][0]=max(f[x][0],f[y][2]+1)\end{array}$$
主要是讨论当有$i$条边与根相邻的情况下子节点有多少条边相邻的限制。
当$i=0$时，子节点有多少边相邻都没关系，那就取尽量小的。
当$i=1$时，要分类是否与这个子节点相连的边被选择，若被选择这个子节点就只能有1条边连出去，否则依然取最小
当$i=2$时和$i=1$时基本一样，只不过会有两个子节点需要相邻。
因为我们设的是“不多于$i(0\le x\le 2)$条选择的边”，所以还要有
$$\{\begin{array}{c}f[x][1]=min(f[x][1],f[x][0])\\ f[x][2]=min(f[x][2],f[x][1])\end{array}$$
这样第一问的答案就是$f[1][2]$了。

---

第二问要求的是方案数。
设$g[x][j][i]$表示在以$x$为根的子树内，子节点的不便利值都不超过$j$，有不多于$i(0\le x\le 2)$条选择的边与$x$相邻的方案数。
可以证明（但是显然我不会$qwq$）第一问的答案必然小于等于${\log }_{3}n$，所以第2维其实是很小的，可以保证空间。
依然分三种情况讨论
$$\{\begin{array}{c}g[x][j][2]=g[x][j][2]\times g[y][j-1][2]+g[x][j][1]\times g[y][j][1]\\ g[x][j][1]=g[x][j][1]\times g[y][j-1][2]+g[x][j][0]\times g[y][j][1]\\ g[x][j][0]=g[x][j][0]\times g[y][j-1][2]\end{array}$$
当$i=0$时，方案数显然就是每一个子树都连两条边的方案数之积。
当$i=1$或$i=2$时，方案数就是其中1,2条边与子节点连接，其他全部为子节点的方案数之积。
其实$g$的方程和$f$的方程及其相似。
还是那样，最终取一个$min$
$$\{\begin{array}{c}g[x][i][1]=g[x][i][1]+g[x][i][0]\\ g[x][i][2]=g[x][i][2]+g[x][i][1]\end{array}$$
最终第二问答案就是$g[1][f[1][2]][2]$。
总时间复杂度$O(n)$

---

代码：

#include 
#include 
#include 
using namespace std;
typedef long long ll;

const int N=100010;
const ll Inf=1e17;
int n,m,tot,head[N];
ll f[N][3],g[N][15][3],MOD;

struct edge
{
	int next,to;
}e[N*2];

void add(int from,int to)
{
	e[++tot].to=to;
	e[tot].next=head[from];
	head[from]=tot;
}

void dp1(int x,int fa)
{
	f[x][0]=1; f[x][1]=Inf; f[x][2]=Inf;
	for (int i=head[x];~i;i=e[i].next)
	{
		int y=e[i].to;
		if (y!=fa)
		{
			dp1(y,x);
			f[x][2]=min(max(f[x][2],f[y][2]+1),max(f[x][1],f[y][1]));
			f[x][1]=min(max(f[x][1],f[y][2]+1),max(f[x][0],f[y][1]));
			f[x][0]=max(f[x][0],f[y][2]+1);
		}
	}
	f[x][1]=min(f[x][1],f[x][0]);
	f[x][2]=min(f[x][2],f[x][1]);
}

void dp2(int x,int fa)
{
	for (int i=1;i<=f[1][2];i++)
		g[x][i][0]=1;
	for (int i=head[x];~i;i=e[i].next)
	{
		int y=e[i].to;
		if (y!=fa)
		{
			dp2(y,x);
			for (int j=1;j<=f[1][2];j++)
			{
				g[x][j][2]=(g[x][j][2]*g[y][j-1][2]+g[x][j][1]*g[y][j][1])%MOD;
				g[x][j][1]=(g[x][j][1]*g[y][j-1][2]+g[x][j][0]*g[y][j][1])%MOD;
				g[x][j][0]=(g[x][j][0]*g[y][j-1][2])%MOD;
			}
		}
	}
	for (int i=1;i<=f[1][2];i++)
	{
		g[x][i][1]=(g[x][i][1]+g[x][i][0])%MOD;
		g[x][i][2]=(g[x][i][2]+g[x][i][1])%MOD;
	}
}

int main()
{
	memset(head,-1,sizeof(head));
	scanf("%d%d%lld",&n,&m,&MOD);
	if (m!=n-1) return !printf("-1\n-1");
	for (int i=1,x,y;i<=m;i++)
	{
		scanf("%d%d",&x,&y);
		add(x,y); add(y,x);
	}
	dp1(1,0); 
	dp2(1,0);
	printf("%lld\n%lld",f[1][2]-1,g[1][f[1][2]][2]);
	return 0;
}