删边最小生成树
删边最小生成树
时间限制: 1 Sec 内存限制: 128 MB
题目描述
给定一个n个点m条边的无向图,求删除某条之后的最小生成树。
输入
第一行两个整数n和m。
接下来m行,每行3个整数a、b、c
表示有条边连接编号为a和b的节点。输出
输出m行,每行一个整数。
表示如果第i条删除,最小生成树的大小,如果最小生成树不存在,输出-1。样例输入
5 5
1 2 1
2 3 2
1 4 3
2 4 5
4 5 4样例输出
14
-1
12
10
-1提示
30%的数据,n的范围[1,100],m的范围[1,1000];
50%的数据,n的范围[1,300],m的范围[1,3000];
80%的数据,n的范围[1,5000],m的范围[1,50000];
100%的数据,n的范围[1,50000],m的范围[1,200000],边权范围[1,40000];
暴力枚举
int find(int x){
if(x==par[x])return x;
return par[x]=find(par[x]);
}
void check(int x){
int res=n,sum=0;
for(int i=1;i<=n;i++)par[i]=i;
for(int i=1;i<=m&&res!=1;i++){
if(i==x)continue;
a=s[i].a,c=s[i].c,b=s[i].b;
fa=find(a),fb=find(b);
if(fa==fb)continue;
par[fa]=fb;sum+=c;res--;
}ans[s[x].id]=res==1?sum:-1;
}
void solve(){
sort(s+1,s+1+m,cmp);
for(int i=1;i<=m;i++){
if(!mark[s[i].id])ans[s[i].id]=pro_sum;
else check(i);
}
}思路
对于树而言它是无环的

如果加上一条边nw它就形成了一个环
对于环上的任意的一条边删去其中之一它仍为树
即nw可以代替该环上的任意边
那么对于最小生成树而言删去它的代价即为val[x]-val[nw];
所以删可以更新环上任意一条边的答案
显然加入的边要从小到大同时有答案的边无需更新
首先生成最小生成树
void made(){
sort(E+1,E+1+m,cmp);
int res=n,a,b,c,id,fa,fb;
for(int i=1;i<=m&&res!=1;i++){
a=E[i].a;b=E[i].b;
c=E[i].c;id=E[i].id;
fa=find(a);fb=find(b);
if(fa==fb)continue;
G[a].push_back((P){b,c,id});
G[b].push_back((P){a,c,id});
//生成最小生成树
sum+=c;res--;
par[fa]=fb;mark[id]=1;
}d[1]=1;
dfs(1);
}那么如何遍历环呢?;
先预处理出所以的节点的父节点以及其对应的边的边号和代价
void dfs(int x){
for(int i=0;ito=G[x][i].t;c=G[x][i].c;id=G[x][i].id;
if(!d[to]){
d[to]=d[x]+1;
f[to]=x;dfs(to);
td[to]=id;tc[to]=c;//记录该节点对应的边的id和c
}
}
} void update(int a,int b){
if(d[a]>d[b])swap(a,b);
while(d[a]id=td[b];c=tc[b];//从节点获取对应的边的id和c
if(!use[id])ans[id]=sum-c+cost,use[id]=1;
b=f[b];
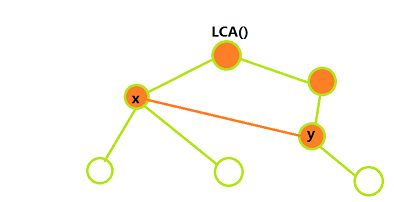
}while(a!=b){
//一直遍历到LCA(a,b);
id=td[b];c=tc[b];
if(!use[id])ans[id]=sum-c+cost,use[id]=1;
b=f[b];
id=td[a];c=tc[a];
if(!use[id])ans[id]=sum-c+cost,use[id]=1;
a=f[a];
}
} void solve(){
for(int i=1;i<=m;i++)
if(!mark[E[i].id]){
a=E[i].a;b=E[i].b;c=E[i].c;
cost=c;update(a,b);
}for(int i=1;i<=m;i++){
if(!mark[i])printf("%d\n",sum);
else printf("%d\n",ans[i]);
}return 0;
}综上;
#include.c;}
vector G[M];
int par[M],f[M],n,m,sum,d[M];
int td[M],tc[M],cost,ans[4*M];
bool mark[4*M],use[4*M];
int find(int x){
if(x==par[x])return x;
return par[x]=find(par[x]);
}
void dfs(int x){
int to,c,id;
for(int i=0;i.size();i++){
to=G[x][i].t;
c=G[x][i].c;
id=G[x][i].id;
if(!d[to]){
d[to]=d[x]+1;
td[to]=id;tc[to]=c;
f[to]=x;
dfs(to);
}
}
}
void update(int a,int b){
int id,c;
if(d[a]>d[b])swap(a,b);
while(d[a]id=td[b];c=tc[b];
if(!use[id])ans[id]=sum-c+cost,use[id]=1;
b=f[b];
}while(a!=b){
id=td[b];c=tc[b];
if(!use[id])ans[id]=sum-c+cost,use[id]=1;
b=f[b];
id=td[a];c=tc[a];
if(!use[id])ans[id]=sum-c+cost,use[id]=1;
a=f[a];
}
}
void made(){
sort(E+1,E+1+m,cmp);
int res=n,a,b,c,id,fa,fb;
for(int i=1;i<=m&&res!=1;i++){
a=E[i].a;b=E[i].b;
c=E[i].c;id=E[i].id;
fa=find(a);fb=find(b);
if(fa==fb)continue;
G[a].push_back((P){b,c,id});
G[b].push_back((P){a,c,id});
sum+=c;res--;
par[fa]=fb;mark[id]=1;
}d[1]=1;
dfs(1);
}
int main(){
int a,b,c,id;
memset(ans,-1,sizeof(ans));
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d%d%d",&a,&b,&c);
E[i]=(node){a,b,c,i};
}
for(int i=1;i<=n;i++)par[i]=i;
made();
for(int i=1;i<=m;i++)
if(!mark[E[i].id]){
a=E[i].a;b=E[i].b;c=E[i].c;
cost=c;update(a,b);
}for(int i=1;i<=m;i++){
if(!mark[i])printf("%d\n",sum);
else printf("%d\n",ans[i]);
}return 0;
}