1.Max sum plus plus
本题是一个M段子段的最大字段和的问题，也就是把一个数列分成M小节使得每小节总和最大。关于这个问题先从最大子段和（单段）开始说起。
最大子段和（子段是连续子数列）的求解意味着对于数列中一个元素，要么归于前面已经成型的一个子段，要么自成一派创立新的子段。这个抉择取决于这两个的权值的大小，如果成型的子段的和较大，那么就让它加入前面的子段，否则就自己作为新子段的开头。
方程：DP[I]=MAX(DP[I-1]+A[I],A[I])
M子段的最大子段和问题是最大子段和的一个推广，与之类似的有最大子矩阵问题。
如果要求解M段子段，那么对于数列内任意一个元素也是都有两种选择：归于前面的第i段或者独树一帜，找到第i-1段的最大值所在并传承过来，然后自己作为第i段的起点。
即为：DP[I][J]=MAX(DP[I][J-1],DP[I-1][SOMEWHERE])+CURRENT[J]，其中DP[I][J]代表当前已经组建了I段，遍历到第J个元素。SOMEWHERE是第i-1段的最大值所在处。
不过对于本题而言，m的大小是一个悬而未决的问题（题目没给），并且n达到了百万级，所以单纯使用上述方程是在内存限制条件下无法求解本题的。所以就要优化空间。
优化空间不是随意的。比如本题使用的滚动数组的优化条件就是当前状态并没有与太多状态相关联，比如说用多少枚硬币表示多少现金，这个DP[I][J]就是无法优化的，因为硬币面值的不同，现金的总额可以由很多状态转移而来，倘若优化就直接破坏了这个数组的信息存储能力，因为很多状态的信息无法被正确的表达，而子状态的信息存储是DP的核心。
幸运的是，通过分析可以发现本题中的状态转移规律，总是可以发现一个事情：当分析某个元素时，这个元素要么归于前面一个子段，要么自己创立一个子段，它跟第i-2及以前的子段没有直接关系，所以可以直接把代表字段数的第一维压缩为一个指示标志：0与1，分别代表两个不同的子段。
得到了一个新的方程：DP[1][J]=MAX(DP[1][J-1],DP[0][K])+CURRENT[I]。
在实现过程中，t（当前段）和1-t（前一段）需要更迭，以达成每一段都可以被访问的目的。
模板：
import java.util.*;
import java.io.*;
import java.math.*;
import java.text.*;
public class Main
{
static int ar[]=new int[15000];
static long dp[][]=new long[3][15000];
public static void main(String args[])throws IOException
{
BufferedReader bf=new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw=new BufferedWriter(new OutputStreamWriter(System.out),1<<16);
String tmp=bf.readLine();
String tmps[]=tmp.trim().split(" ");
int n=Integer.parseInt(tmps[0]),m=Integer.parseInt(tmps[1]);
for(int i=1;i<=n;i++)
{
tmp=bf.readLine();
ar[i]=Integer.parseInt(tmp);
}
int current=1;
for(int i=1;i<=m;i++)
{
dp[current][i]=dp[1-current][i-1]+ar[i];//意味着这是以第m段开始，第一个元素是ar[i]
long tmp9=dp[1-current][i-1];//初始化最大值
for(int j=i+1;j<=n-m+i（一个子段的长度顶多为n-m）;j++)
{
tmp9=Math.max(tmp9,dp[1-current][j-1]);//上一段至j-1之前的最大值
dp[current][j]=Math.max(tmp9,dp[current][j-1])+ar[j];
}
current=1-current;
}
long ans=-1000000002;
for(int i=1;i<=n;i++)
ans=Math.max(ans,Math.max(dp[0][i],dp[1][i]));
bw.write(Long.toString(ans));
bw.newLine();
bw.flush();
bw.close();
}
}
可以看出，尽管DP[0][K]的K下标是一个不定值，但是它本身一定代表着在J-1之前的i-1段的最大值。所以如果在过程中就记录这个最大值，就可以直接略去遍历K次这个环节。如何实现？用一个新数组表示在分成I段时前J-1个元素中所计算出的最大I字段和，然后状态转移方程就变成了DP[1][J]=MAX[DP[1][J-1],PREVIOUS[J-1])+CURRENT[I]
显然前面这个1已经没用了，可以直接压缩掉，最终的方程就是DP[J]=MAX(DP[J-1],PREVIOUS[J-1]),其中previous数组代表分成i-1段时J-1个元素内的最大值，也就是原来的DP[I-1][K].
不过滚动数组意味着多次覆盖，所以如果要准确的求某个状态对应的值（已知两个下标求值），还是慎用此优化。
//#include
#include
#include
#include
#include
#include
3 Monkey and Banana
A group of researchers are designing an experiment to test the IQ of a monkey. They will hang a banana at the roof of a building, and at the mean time, provide the monkey with some blocks. If the monkey is clever enough, it shall be able to reach the banana by placing one block on the top another to build a tower and climb up to get its favorite food.
一队研究员正在设计一个测量猴子智商的实验方案。他们把一个香蕉挂在一个建筑物的屋顶上，与此同时研究员给猴子扔了一堆石头。如果猴子足够聪明的话，它应该能够到香蕉，通过把一个石头垒在另一个石头上并爬到顶上的方式。
The researchers have n types of blocks, and an unlimited supply of blocks of each type. Each type-i block was a rectangular solid with linear dimensions (xi, yi, zi). A block could be reoriented so that any two of its three dimensions determined the dimensions of the base and the other dimension was the height.
研究员有n种石头，以及这几种石头的无限制供应，每种石头都是一个矩形固体块，它们的线性三维数据是xi,yi,zi。一个石头可以换个方向放置，所以它的任意两维都可以指代底面积，另一维指代高。
They want to make sure that the tallest tower possible by stacking blocks can reach the roof. The problem is that, in building a tower, one block could only be placed on top of another block as long as the two base dimensions of the upper block were both strictly smaller than the corresponding base dimensions of the lower block because there has to be some space for the monkey to step on. This meant, for example, that blocks oriented to have equal-sized bases couldn't be stacked.
他们想确认垒石头能到达的最大高度。问题是，垒石头的时候，一个石头只能垒在一个长宽都比他大的石头上。因为这需要留点空间让猴子能踩着上去。比如，这意味着相同底面积的石块不能放在一起。
本题像是那种矩形嵌套的DAG模型，但实际上也可以当做最长上升子序列问题解决。由于石头可以任意放置，所以根据放置的不同，一个石头就有了六种属性，因为石头是无限制供应的，所以这六种可能性可以直接当作六种不同的石头即可。
然后根据长宽降序排序，利用LIS相关知识解决即可。
#include
#include
#include
#include
#include
#include
上面说到DAG，那么这个题同样可以用记忆化搜索解答，利用一个数组标记好嵌套关系，然后从每一个石头开始进行dfs，求最值即可。
#include
#include
#include
#include
#include
#include
5.doing Homework
gnatius has just come back school from the 30th ACM/ICPC. Now he has a lot of homework to do. Every teacher gives him a deadline of handing in the homework. If Ignatius hands in the homework after the deadline, the teacher will reduce his score of the final test, 1 day for 1 point. And as you know, doing homework always takes a long time. So Ignatius wants you to help him to arrange the order of doing homework to minimize the reduced score.
IG已经从第30届ICPC凯旋归校。现在他有一堆作业要做。每个老师都给了他一个交作业的最后期限。如果IG在最后期限后交作业，那么老师就会给他期末扣分，晚一天扣一分。正如你所知道的，做作业一般都要花很长时间。所以IG想让你帮助他规划一下做作业的顺序去最小化扣分数。
如果用一般状态转移的方式来考虑这个问题，就会陷入混乱，因为没有明显且确定的先后顺序（否则直接一个贪心就能做），所以如果强行找状态转移方程的话会非常难。
这实际是一个不明显的二进制状态压缩DP，不过N的数据范围给了我们枚举的提示。只不过由于需要输出方案的原因，这里的状态压缩数组除了当前时间和扣分数之外需要多包含几个信息：当前课程号和前一个课程号。（不推荐用多维数组）
状态压缩的核心在于用二进制01串代表一连串状态，那么状态之间的转移也就是01串上的数字变动。比如这个题，当你确定一个01串（比如0111），并确认某一科的作业已经写了（比如说0111的第二位是1），那么它前一个状态就是这科作业没写的状态（按照刚才的例子，也就是0101），利用这两个状态建立起的关系来传递信息，是状态压缩DP的基本方案。
最后一个dfs沿着标记查询方案即可。
所以思路如下：
1.初始化状态转移数组的所有信息并特别初始化起始状态。
2.利用枚举的01串和其中1的位置，找到对应的科目，并和与现在状态相连的“前状态”构建关系，传输信息
3.dfs找到方案
#include
#include
#include
#include
#include
#include
（记忆化搜索待填坑）
5 super jumping jumping jumping
Nowadays, a kind of chess game called “Super Jumping! Jumping! Jumping!” is very popular in HDU. Maybe you are a good boy, and know little about this game, so I introduce it to you now.
现如今，一种叫做超级跳跳跳的棋类游戏在杭电相当盛行。可能你是个优秀的人，但是不大了解这个游戏，所以我现在给你介绍一下。
The game can be played by two or more than two players. It consists of a chessboard（棋盘）and some chessmen（棋子）, and all chessmen are marked by a positive integer or “start” or “end”. The player starts from start-point and must jumps into end-point finally. In the course of jumping, the player will visit the chessmen in the path, but everyone must jumps from one chessman to another absolutely bigger (you can assume start-point is a minimum and end-point is a maximum.). And all players cannot go backwards. One jumping can go from a chessman to next, also can go across many chessmen, and even you can straightly get to end-point from start-point. Of course you get zero point in this situation. A player is a winner if and only if he can get a bigger score according to his jumping solution. Note that your score comes from the sum of value on the chessmen in you jumping path.
这个游戏可以有两个或以上的玩家。它包含一个棋盘和一些棋子，以及所有的棋子都由一个正整数或者start和end标记。玩家由起点开始，最后必须跳到终点处。跳跃的时候，玩家会和路径中的棋子碰面，但是每个人必须跳到一个棋子标号严格大于当前棋子的棋子上。并且跳过去之后不能回头。一次跳跃可以跳到相邻的棋子，也可以越过很多棋子，直接到达终点也行。当然你这么做就只能得零分。一个玩家获胜的条件是他的跳跃方案可以得到更多分。你的分数由你的路径中的棋子标号的和决定。
Your task is to output the maximum value according to the given chessmen list.
请找出最大值。
最长上升子序列模板题，记忆化搜索和普通递推皆可。
//#include
#include
#include
#include
#include
#include
6 免费馅饼
本题乍一看没有什么很明显的思路，但是当分析样例之后会发现一个很有趣的事情
答案是4
同一时间内的馅饼只能捡一个，而且在某一位置只能向两边移动。像不像入门时候的数字三角形？？
那么状态转移方程也是类似的：dp[i][j]=max(dp[i+1][j],max(dp[i+1][j+1],dp[i+1][j-1]))，第一维是当前时间，第二维是当前位置。
#include
#include
#include
#include
#include
#include
Tickets
Jesus, what a great movie! Thousands of people are rushing to the cinema. However, this is really a tuff time for Joe who sells the film tickets. He is wandering when could he go back home as early as possible.
老天爷，这电影真好看。数以千计的群众涌入电影院。但是，这对于卖票的JOE来说却是一个难熬的日子。他想知道他啥时候能尽早回家。
A good approach, reducing the total time of tickets selling, is let adjacent people buy tickets together. As the restriction of the Ticket Seller Machine, Joe can sell a single ticket or two adjacent tickets at a time.
一个减少买票时间的好办法就是让相邻的人一块买票。由于售票机的一个限制 ，JOE一次只能卖一张票或是两张相邻的票。
Since you are the great JESUS, you know exactly how much time needed for every person to buy a single ticket or two tickets for him/her. Could you so kind to tell poor Joe at what time could he go back home as early as possible? If so, I guess Joe would full of appreciation for your help.
因为你是全能的上帝。你知道每个人买一张票或者是相邻的人买两张票需要多久。你能告诉可怜的JOE他啥时候才能回家吗。如果能，我猜JOE会对你的帮助充满感激。
对于每一个人来说，要么他们单独买票，要么他们和前面一人一起买票，所以可以假设状态转移数组DP的唯一一维指的是当前买票的人，也就是第几个买票的。就有状态转移方程：dp[i]=max(dp[i-1]+single[i]+dp[i-2]+adjacent[i])(i>=2)
因为只有一个人的时候只能单独买票，所以直接令dp[1]=single[1]即可。
本题可用记忆化搜索和递推两种方式解题，记忆化搜索需要从后往前递推，然后利用回溯解决问题，而使用递推式直接从前往后求解即可。
import java.io.*;
import java.util.*;
import java.math.*;
import java.text.*;
public class Main40
{
static int single[]=new int[50000];
static int adjacent[]=new int[50000];
static int dp[]=new int[50000];
public static int dfs(int current)
{
if(dp[current]>0)
return dp[current];
else if(current==1)
return dp[current]=single[current];//dp[1]=single[1]
else if(current==0)//这个边界有必要处理，0是还没有人买票的状态。
return dp[current]=0;
else
{
int ans1=5999996,ans2=5999996;
if(current>=2)
ans1=dfs(current-2)+adjacent[current];
if(current>=1)
ans2=dfs(current-1)+single[current];
//System.out.println(ans1+" "+ans2);
return dp[current]=Math.min(ans1,ans2);
}
}
public static void main(String args[])throws IOException
{
StreamTokenizer st=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
PrintWriter pw=new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
int scenario;
st.nextToken();scenario=(int)st.nval;
for(int i=1;i<=scenario;i++)
{
st.nextToken();
int n=(int)st.nval;
for(int u=1;u<=n+5;u++)
dp[u]=0;
for(int j=1;j<=n;j++)
{
st.nextToken();single[j]=(int)st.nval;
}
for(int j=2;j<=n;j++)
{
st.nextToken();adjacent[j]=(int)st.nval;
}
int ans=dfs(n);
//pw.println(ans);
int hour=8+ans/3600,minute=0+ans%3600/60,second=0+ans%60;
boolean isam=true;
if(hour>=12)
isam=false;
DecimalFormat df=new DecimalFormat("00");
pw.println(df.format(hour)+":"+df.format(minute)+":"+df.format(second)+(isam==true?" am":" pm"));
pw.flush();
}
pw.close();
}
}
FatMouse's Speed
FatMouse believes that the fatter a mouse is, the faster it runs. To disprove this, you want to take the data on a collection of mice and put as large a subset of this data as possible into a sequence so that the weights are increasing, but the speeds are decreasing.
硕鼠认为老鼠越胖就跑得越快。为了证伪这个观点，你想去找一个关于老鼠信息的数据集并且在里边找一个最大的子集，这个子集里的老鼠的体重信息是递增的，但是速度信息是递减的。
很明显这是一个最长上升（下降）子序列的问题，但是有两维。可以用贪心直接解决掉一维，即直接对一维进行排序，使得它满足所需的顺序。然后对于另一维，就可以用普通的平方级LIS算法解出所需的最长上升子序列的长度和路径，最后用dfs回溯即可。
值得注意的是输入数据的时候不要用cin，因为未知原因，cin在这里无法判断EOF。
#include
#include
#include
#include
#include
#include
POJ3186
这是一个区间动态规划。
因为题给的背景是一个是两头出不能进的的模型，可以看做双端队列。针对于每一次的操作而言，要么是拿左边的，要么是拿右边的，也可以一直拿左边，或者一直拿右边，剩余的物品数目的范围的首尾约束使用普通的状态转移很难做到，所以这里直接考虑区间DP——以区间长度为准则之一的动态规划法。
因为一个连续的区间比两个分割的区间好维护，所以这里选择剩余的物品个数作区间长度。已经知道了区间长度，只需要再次枚举起点，就可以得知终点的位置，接下来就是直接状态转移：在本区间内，是拿左侧的物品，还是拿右侧的物品。
值得一说的是要初始化，即假设所有物品都是最后一个拿的情况（针对它自己这个区间而言）。
ll arr[2323];
ll dp[2500][2500];
int DETERMINATION()
{
std::ios::sync_with_stdio(false);
std::cin.tie(0),std::cout.tie(0);
ll n;
cin>>n;
for(int i=1;i<=n;i++)
cin>>arr[i];
for(int i=1;i<=n;i++)
dp[i][i]=arr[i]*n;
for(int interval=1;interval<=n;interval++)
{
for(int i=1;i+interval<=n;i++)
{
ll upper=i+interval;
dp[i][upper]=max(dp[i+1][upper]+arr[i]*(n-interval),dp[i][upper-1]+arr[upper]*(n-interval));
}
}
cout<
POJ3616
这是一个线性DP，可以理解为最长上升子序列。这也就相当于判断在时间维度上，某个区间之前的区间是否可以接在这个区间前面，基本上就是求m个数的最长上升子序列。
初始化：就是每个区间本身的权值，即最长上升子序列只有一个元素的时候。
struct node
{
ll st,ed,value;
}nodes[5999];
ll dp[2000];
bool cmp(node a,node b)
{
if(a.st!=b.st)
return a.st>n>>m>>r;
for(int i=1;i<=m;i++)
cin>>nodes[i].st>>nodes[i].ed>>nodes[i].value;
sort(nodes+1,nodes+1+m,cmp);
for(int i=1;i<=m;i++)
dp[i]=nodes[i].value;
ll ans=0;
for(int i=1;i<=m;i++)
{
for(int j=1;j
POJ3666
这个题是把给定的一个序列修改一定的数量使得它们非递减。
首先，对于任意正整数集合A，一定存在一组解，即所有Bi∈A，使得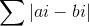
最小。这就把“标准值”的枚举范围缩小到了集合A的所有数，但是A的最大值仍然无法在限定内存内用数组下标表示，所以对此再进行一步离散化，并用离散化后的序号作索引，即：离散化后索引->离散化前的值。
因为对于某个状态而言它只和自身与前一个状态有关，所以可以考虑滚动数组优化。
//#include
#include
#include
//#include
#include
#include
HDU1078
由于这个老鼠可以走回头路，所以一般的从左上到右下的递推是行不通的。这个时候就要用到bfs式记忆化搜索来解决这个恼人的遍历图的问题。
在过程中需要回溯前k个进度，也就是说以当前位置，k为半径的一个圆（在曼哈顿距离约束下应当是一个矩形。）所以在每次到达一个地方时需要从这一堆可能的区域内找出一个最大值，使之承接到现在的状态上。
//#include
#include
#include
#include
#include
#include
HDU2859
这个题里要求一个最大对称方阵。对于初始矩阵从左下到右上的对角线上的任意一点，它要么继承前一个点的对称矩阵，要么另起炉灶再开一个新的对称矩阵。所以说对于每一个点而言都需要讨论一下从这个点是否可以延伸出前一个所能扩展的对称矩阵的边长，如果完全可以从上一个点顺承下来，就直接在前一个点的答案上加一，反之把从这个点扩展出来的子矩阵边长记录下来。
//#include
#include
#include
#include
#include
#include
