2020.8.7【算协集训】并查集&最小生成树

网页链接：传送门
密码：hpuacm

A - Highways (POJ-2485)

The island nation of Flatopia is perfectly flat. Unfortunately, Flatopia has no public highways. So the traffic is difficult in Flatopia. The Flatopian government is aware of this problem. They’re planning to build some highways so that it will be possible to drive between any pair of towns without leaving the highway system.
Flatopian towns are numbered from 1 to N. Each highway connects exactly two towns. All highways follow straight lines. All highways can be used in both directions. Highways can freely cross each other, but a driver can only switch between highways at a town that is located at the end of both highways.
The Flatopian government wants to minimize the length of the longest highway to be built. However, they want to guarantee that every town is highway-reachable from every other town.
Input
The first line of input is an integer T, which tells how many test cases followed.
The first line of each case is an integer N (3 <= N <= 500), which is the number of villages. Then come N lines, the i-th of which contains N integers, and the j-th of these N integers is the distance (the distance should be an integer within [1, 65536]) between village i and village j. There is an empty line after each test case.
Output
For each test case, you should output a line contains an integer, which is the length of the longest road to be built such that all the villages are connected, and this value is minimum.

Sample Input	Sample Output	Hint
1 3 0 990 692 990 0 179 692 179 0	692	Huge input,scanf is recommended.

分析

有 $T$ 组测试用例。每组测试用例开头包含一个整数 $N$ ，代表有 $N$ 个城市（城市编号 $\in [1,N]$ ）。下面共有 $N$ 行 $N$ 列， $i$ 行 $j$ 列代表城市 $i$ 到城市 $j$ 的距离。如果能有一条铁路线连接所有城市，问你这条铁路线最长的边最小是多少？

其实就是问最小生成树的最大边是多少。

代码

#include
#include
using namespace std;
typedef long long ll;
const ll maxn=510;

int T,N,tt,len,mx;
int fa[maxn];

struct node	//结构体存边
{
	int from,to,dist;
	bool operator < (const node & other) const
	{
		return dist<other.dist; 
	}
}e[maxn*maxn];	//这个要开大点

int findfa(int x)	//寻找父亲节点
{
	if(fa[x]!=x)	return fa[x]=findfa(fa[x]);
	return fa[x];
}

void merge(int x,int y)	//合并
{
	x=findfa(x);
	y=findfa(y);
	fa[y]=x;	//更新父亲节点
}

int main()
{
	scanf("%d",&T);
	while(T--)	//T组测试用例
	{
		scanf("%d",&N);
		for(int i=1;i<=N;i++)	//初始化父亲节点
			fa[i]=i;
		tt=mx=0;
		for(int i=1;i<=N;i++)	//存放两个城市之间的边
		{
			for(int j=1;j<=N;j++)
			{
				scanf("%d",&len);
				if(i==j)	continue;	//自己到自己没必要存噻
				e[tt].from=i;
				e[tt].to=j;
				e[tt++].dist=len;
			}
		}
		sort(e,e+tt);
		for(int i=0;i<tt;i++)
		{
			int fafrom=findfa(e[i].from);
			int fato=findfa(e[i].to);
			if(fafrom!=fato)
			{
				merge(e[i].from,e[i].to);
				if(e[i].dist>mx)	mx=e[i].dist;	//更新最小生成树上最大边的值
			}
		}
		printf("%d\n",mx);
	}
	return 0;
}

---

B - Networking (POJ-1287)

You are assigned to design network connections between certain points in a wide area. You are given a set of points in the area, and a set of possible routes for the cables that may connect pairs of points. For each possible route between two points, you are given the length of the cable that is needed to connect the points over that route. Note that there may exist many possible routes between two given points. It is assumed that the given possible routes connect (directly or indirectly) each two points in the area.
Your task is to design the network for the area, so that there is a connection (direct or indirect) between every two points (i.e., all the points are interconnected, but not necessarily by a direct cable), and that the total length of the used cable is minimal.
Input
The input file consists of a number of data sets. Each data set defines one required network. The first line of the set contains two integers: the first defines the number P of the given points, and the second the number R of given routes between the points. The following R lines define the given routes between the points, each giving three integer numbers: the first two numbers identify the points, and the third gives the length of the route. The numbers are separated with white spaces. A data set giving only one number P=0 denotes the end of the input. The data sets are separated with an empty line.
The maximal number of points is 50. The maximal length of a given route is 100. The number of possible routes is unlimited. The nodes are identified with integers between 1 and P (inclusive). The routes between two points i and j may be given as i j or as j i.
Output
For each data set, print one number on a separate line that gives the total length of the cable used for the entire designed network.

Sample Input	Sample Output
1 0 2 3 1 2 37 2 1 17 1 2 68 3 7 1 2 19 2 3 11 3 1 7 1 3 5 2 3 89 3 1 91 1 2 32 5 7 1 2 5 2 3 7 2 4 8 4 5 11 3 5 10 1 5 6 4 2 12 0	0 17 16 26

分析

有 $P$ 个点和 $R$ 条路径。 $P=0$ 时代表输入结束。问你连接所有点的最小路径总长度是多少。
其实就是问最小生成树的边权之和是多少。

和上题最大的区别就是一个是求最大值一个是求和，其他除了输入部分外几乎没有区别。

代码

#include
#include
using namespace std;
typedef long long ll;
const ll maxn=55;

int P,R,tt,u,v,w,sum;
int fa[maxn];

struct node	//结构体存边
{
	int from,to,dist;
	bool operator < (const node & other) const
	{
		return dist<other.dist; 
	}
}e[maxn*maxn];

int findfa(int x)	//寻找父亲节点
{
	if(fa[x]!=x)	return fa[x]=findfa(fa[x]);
	return fa[x];
}

void merge(int x,int y)	//合并
{
	x=findfa(x);
	y=findfa(y);
	fa[y]=x;	//更新父亲节点
}

int main()
{
	while(~scanf("%d",&P))
	{
		if(P==0)	break;
		scanf("%d",&R);
		for(int i=1;i<=P;i++)	//初始化父亲节点
			fa[i]=i;
		tt=sum=0;
		for(int i=1;i<=R;i++)
		{
			scanf("%d%d%d",&u,&v,&w);
			e[tt].from=u;
			e[tt].to=v;
			e[tt++].dist=w;
		}
		sort(e,e+tt);
		for(int i=0;i<tt;i++)
		{
			int fafrom=findfa(e[i].from);
			int fato=findfa(e[i].to);
			if(fafrom!=fato)
			{
				merge(e[i].from,e[i].to);
				sum+=e[i].dist;	//更新最小生成树上边权之和 
			}
		}
		printf("%d\n",sum);
	}
	return 0;
}

---

C - The Suspects (POJ-1611)

Severe acute respiratory syndrome (SARS), an atypical pneumonia of unknown aetiology, was recognized as a global threat in mid-March 2003. To minimize transmission to others, the best strategy is to separate the suspects from others.
In the Not-Spreading-Your-Sickness University (NSYSU), there are many student groups. Students in the same group intercommunicate with each other frequently, and a student may join several groups. To prevent the possible transmissions of SARS, the NSYSU collects the member lists of all student groups, and makes the following rule in their standard operation procedure (SOP).
Once a member in a group is a suspect, all members in the group are suspects.
However, they find that it is not easy to identify all the suspects when a student is recognized as a suspect. Your job is to write a program which finds all the suspects.
Input
The input file contains several cases. Each test case begins with two integers n and m in a line, where n is the number of students, and m is the number of groups. You may assume that 0 < n <= 30000 and 0 <= m <= 500. Every student is numbered by a unique integer between 0 and n−1, and initially student 0 is recognized as a suspect in all the cases. This line is followed by m member lists of the groups, one line per group. Each line begins with an integer k by itself representing the number of members in the group. Following the number of members, there are k integers representing the students in this group. All the integers in a line are separated by at least one space.
A case with n = 0 and m = 0 indicates the end of the input, and need not be processed.
Output
For each case, output the number of suspects in one line.

Sample Input	Sample Output
100 4 2 1 2 5 10 13 11 12 14 2 0 1 2 99 2 200 2 1 5 5 1 2 3 4 5 1 0 0 0	4 1 1

分析

有 $n$ 个学生（编号 $\in [0,n-1]$ ），$m$ 个小组，每个学生可能在多个小组里，每个小组都有 $k$ 个成员。一个人疑似感染，整组人就都是疑似感染的。现在知道编号为 $0$ 的学生是疑似感染的人，问你一共有多少个疑似感染者。

这题应该比较明显，就是找他们的父亲节点是否和编号为 $0$ 的学生的父亲节点一致。因此最后只需要遍历每个学生，看看是否一致。一致就增加人数；反之就不增加。

代码

#include
#include
using namespace std;
typedef long long ll;
const ll maxn=30010;

int N,M,K,x,y,sum;
int fa[maxn];

int findfa(int x)	//寻找父亲节点
{
	if(fa[x]!=x)	return fa[x]=findfa(fa[x]);
	return fa[x];
}

void merge(int x,int y)	//合并
{
	x=findfa(x);
	y=findfa(y);
	fa[y]=x;	//更新父亲节点
}

int main()
{
	while(~scanf("%d%d",&N,&M))
	{
		if(N==0 && M==0)	break;
		for(int i=0;i<N;i++)	//初始化父亲节点
			fa[i]=i;
		sum=0;
		for(int i=0;i<M;i++)
		{
			scanf("%d",&K);
			scanf("%d",&x);	//组长 
			for(int j=1;j<K;j++)
			{
				scanf("%d",&y);	//组员 
				merge(x,y);
			}
		}
		for(int i=0;i<N;i++)
		{
			if(findfa(i)==findfa(0))	//i和0的组长一样,说明在同一个组里,都是嫌疑人 
			{
				sum++;
			}
		}
		printf("%d\n",sum);
	}
	return 0;
}

---

D - Cube Stacking (POJ-1988)

Farmer John and Betsy are playing a game with N (1 <= N <= 30,000)identical cubes labeled 1 through N. They start with N stacks, each containing a single cube. Farmer John asks Betsy to perform P (1<= P <= 100,000) operation. There are two types of operations:
moves and counts.
* In a move operation, Farmer John asks Bessie to move the stack containing cube X on top of the stack containing cube Y.
* In a count operation, Farmer John asks Bessie to count the number of cubes on the stack with cube X that are under the cube X and report that value.
Write a program that can verify the results of the game.
Input
* Line 1: A single integer, P
* Lines 2…P+1: Each of these lines describes a legal operation. Line 2 describes the first operation, etc. Each line begins with a ‘M’ for a move operation or a ‘C’ for a count operation. For move operations, the line also contains two integers: X and Y.For count operations, the line also contains a single integer: X.
Note that the value for N does not appear in the input file. No move operation will request a move a stack onto itself.
Output
Print the output from each of the count operations in the same order as the input file.

Sample Input	Sample Output
6 M 1 6 C 1 M 2 4 M 2 6 C 3 C 4	1 0 2

分析

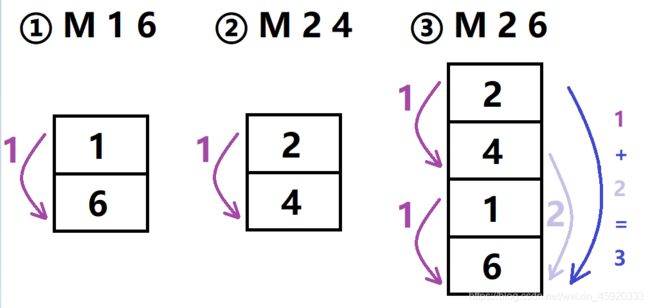
有 $N$ 个立方体（编号 $\in [1,N]$ ）和 $N$ 个格子。一开始立方体 $i$ 在格子 $i$ 上，每个格子一个立方体。现在有 $P$ 次操作：输入格式为 $“Mxy”$ ，表示将立方体 $x$ 所在格子上全部立方体放在立方体 $y$ 所在格子的顶部；输入格式为 $“Cx"$ ，表示输出立方体 $x$ 下面的立方体的个数。

这里设定的父节点是每个格子最下面的那个点。$cnt[i]$ 代表 $i$ 到 $fa[i]$ 的距离，即 $i$ 下面的块数；$s[i]$ 代表 $i$ 所在的堆的总块数。

代码

#include
using namespace std;
typedef long long ll;
const ll maxn=30010;

int P,x,y,z,cnt[maxn],s[maxn];	//cnt[i]代表i下面的块数,s[i]代表i所在堆的总块数 
int fa[maxn];
char c;

int findfa(int x)	//寻找父亲节点
{
	if(fa[x]!=x)
	{
		int f=fa[x];	//不能先cnt变化再递归,否则会结果错误(因为在递归的过程中,堆上的每一点的cnt都有可能发生变化,如果一开始就加好再递归,会导致结果错误)
		fa[x]=findfa(fa[x]);
		cnt[x]+=cnt[f];
	}
	return fa[x];
}

void merge(int x,int y)	//合并
{
	x=findfa(x);
	y=findfa(y);
	if(x!=y)
	{
		fa[x]=y;	//更新父亲节点
		cnt[x]=s[y];	//因为x要放在y所在堆的堆顶,x下面的块数就是原堆的总块数 
		s[y]+=s[x];	//y所在堆的总块数增加 
	}
}

int main()
{
	scanf("%d",&P);
	for(int i=1;i<maxn;i++)
	{
		fa[i]=i;	//刚开始父亲节点都是它本身 
		s[i]=1;	//一开始每个堆只有一块立方体 
	}
	while(P--)
	{
		getchar();	//吸收回车 
		scanf("%c",&c);
		if(c=='M')	//将立方体x所在格子上全部立方体放在立方体y所在格子的顶部
		{
			scanf("%d%d",&x,&y);
			merge(x,y);
		}
		else if(c=='C')	//输出立方体x下面的立方体的个数
		{
			scanf("%d",&z);
			findfa(z);
			printf("%d\n",cnt[z]);
		}
	}
	return 0;
}

---

E - 还是畅通工程 (HDU-1233)

某省调查乡村交通状况，得到的统计表中列出了任意两村庄间的距离。省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通（但不一定有直接的公路相连，只要能间接通过公路可达即可），并要求铺设的公路总长度为最小。请计算最小的公路总长度。
Input
测试输入包含若干测试用例。每个测试用例的第1行给出村庄数目N ( < 100 )；随后的N(N-1)/2行对应村庄间的距离，每行给出一对正整数，分别是两个村庄的编号，以及此两村庄间的距离。为简单起见，村庄从1到N编号。
当N为0时，输入结束，该用例不被处理。
Output
对每个测试用例，在1行里输出最小的公路总长度。

Sample Input	Sample Output
3 1 2 1 1 3 2 2 3 4 4 1 2 1 1 3 4 1 4 1 2 3 3 2 4 2 3 4 5 0	3 5

分析

这次就真的几乎和 $B$ 题一模一样了！还是中文题！注意一些地方的数据需要改下就好啦~

代码

#include
#include
using namespace std;
typedef long long ll;
const ll maxn=110;

int N,tt,u,v,w,sum;
int fa[maxn];

struct node	//结构体存边
{
	int from,to,dist;
	bool operator < (const node & other) const
	{
		return dist<other.dist; 
	}
}e[maxn*maxn];

int findfa(int x)	//寻找父亲节点
{
	if(fa[x]!=x)	return fa[x]=findfa(fa[x]);
	return fa[x];
}

void merge(int x,int y)	//合并
{
	x=findfa(x);
	y=findfa(y);
	fa[y]=x;	//更新父亲节点
}

int main()
{
	while(~scanf("%d",&N))
	{
		if(N==0)	break;
		for(int i=1;i<=N;i++)	//初始化父亲节点
			fa[i]=i;
		tt=sum=0;
		for(int i=1;i<=N*(N-1)>>1;i++)
		{
			scanf("%d%d%d",&u,&v,&w);
			e[tt].from=u;
			e[tt].to=v;
			e[tt++].dist=w;
		}
		sort(e,e+tt);
		for(int i=0;i<tt;i++)
		{
			int fafrom=findfa(e[i].from);
			int fato=findfa(e[i].to);
			if(fafrom!=fato)
			{
				merge(e[i].from,e[i].to);
				sum+=e[i].dist;	//更新最小生成树上边权之和 
			}
		}
		printf("%d\n",sum);
	}
	return 0;
}

---

F - 畅通工程 (HDU-1863)

省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通（但不一定有直接的公路相连，只要能间接通过公路可达即可）。经过调查评估，得到的统计表中列出了有可能建设公路的若干条道路的成本。现请你编写程序，计算出全省畅通需要的最低成本。
Input
测试输入包含若干测试用例。每个测试用例的第1行给出评估的道路条数 N、村庄数目M ( < 100 )；随后的 N 行对应村庄间道路的成本，每行给出一对正整数，分别是两个村庄的编号，以及此两村庄间道路的成本（也是正整数）。为简单起见，村庄从1到M编号。当N为0时，全部输入结束，相应的结果不要输出。
Output
对每个测试用例，在1行里输出全省畅通需要的最低成本。若统计数据不足以保证畅通，则输出“?”。

Sample Input	Sample Output
3 3 1 2 1 1 3 2 2 3 4 1 3 2 3 2 0 100	3 ?

分析

这题也和上一题是类似的（七四看名字也知道是类似的了哈）。除了一些需要修改数据的地方，就只增加了一个判断条件。
因为 $M$ 个点至少需要 $M-1$ 条边才能保证图是连通的，所以在计算过程中可以计算连了几条边了，如果边数 $=M-1$ 就说明可以连通；反之则不能连通。

代码

#include
#include
using namespace std;
typedef long long ll;
const ll maxn=110;

int N,M,tt,k,u,v,w,sum;
int fa[maxn];

struct node	//结构体存边
{
	int from,to,cost;
	bool operator < (const node & other) const
	{
		return cost<other.cost; 
	}
}e[maxn*maxn];

int findfa(int x)	//寻找父亲节点
{
	if(fa[x]!=x)	return fa[x]=findfa(fa[x]);
	return fa[x];
}

void merge(int x,int y)	//合并
{
	x=findfa(x);
	y=findfa(y);
	fa[y]=x;	//更新父亲节点
}

int main()
{
	while(~scanf("%d%d",&N,&M))
	{
		if(N==0)	break;
		for(int i=1;i<=M;i++)	//初始化父亲节点
			fa[i]=i;
		tt=k=sum=0;
		for(int i=1;i<=N;i++)
		{
			scanf("%d%d%d",&u,&v,&w);
			e[tt].from=u;
			e[tt].to=v;
			e[tt++].cost=w;
		}
		sort(e,e+tt);
		for(int i=0;i<tt;i++)
		{
			if(k==M-1)	break;	//M个点至少需要M-1条边才能保证连通
			int fafrom=findfa(e[i].from);
			int fato=findfa(e[i].to);
			if(fafrom!=fato)
			{
				merge(e[i].from,e[i].to);
				sum+=e[i].cost;	//更新最小生成树上边权之和 
				k++;	//已连接边数增加
			}
		}
		if(k==M-1)	printf("%d\n",sum);	//是连通图
		else	printf("?\n");	//不是连通图
	}
	return 0;
}

---

G - 畅通工程再续 (HDU-1875)

相信大家都听说一个“百岛湖”的地方吧，百岛湖的居民生活在不同的小岛中，当他们想去其他的小岛时都要通过划小船来实现。现在政府决定大力发展百岛湖，发展首先要解决的问题当然是交通问题，政府决定实现百岛湖的全畅通！经过考察小组RPRush对百岛湖的情况充分了解后，决定在符合条件的小岛间建上桥，所谓符合条件，就是2个小岛之间的距离不能小于10米，也不能大于1000米。当然，为了节省资金，只要求实现任意2个小岛之间有路通即可。其中桥的价格为 100元/米。
Input
输入包括多组数据。输入首先包括一个整数T(T <= 200)，代表有T组数据。
每组数据首先是一个整数C(C <= 100),代表小岛的个数，接下来是C组坐标，代表每个小岛的坐标，这些坐标都是 0 <= x, y <= 1000的整数。
Output
每组输入数据输出一行，代表建桥的最小花费，结果保留一位小数。如果无法实现工程以达到全部畅通，输出”oh!”.

Sample Input	Sample Output
2 2 10 10 20 20 3 1 1 2 2 1000 1000	1414.2 oh!

分析

这题就是前两题的进化版。在判断最后是否是连通图的基础上，还增加了计算两点间的坐标、判断两点间的距离是否合法。

存放每个点的坐标可以用结构体存，计算两点间的距离就是普通的知道两点坐标计算两点距离的公式。合法就存边，不合法就不存。

代码

#include
#include
#include
using namespace std;
typedef long long ll;
const ll maxn=110;

int T,N,tt,k,u,v,w;
double sum;
int fa[maxn];

struct poi
{
	int x,y;
}p[maxn];

double dis(int a,int b)
{
	return sqrt((double)(p[a].x-p[b].x)*(p[a].x-p[b].x)+(p[a].y-p[b].y)*(p[a].y-p[b].y));
}

struct node	//结构体存边
{
	int from,to;
	double cost;
	bool operator < (const node & other) const
	{
		return cost<other.cost; 
	}
}e[maxn*maxn];

int findfa(int x)	//寻找父亲节点
{
	if(fa[x]!=x)	return fa[x]=findfa(fa[x]);
	return fa[x];
}

void merge(int x,int y)	//合并
{
	x=findfa(x);
	y=findfa(y);
	fa[y]=x;	//更新父亲节点
}

int main()
{
	scanf("%d",&T);
	while(T--)
	{
		for(int i=0;i<maxn;i++)	//初始化父亲节点
			fa[i]=i;
		tt=k=sum=0;
		scanf("%d",&N);
		for(int i=1;i<=N;i++)
		{
			scanf("%d%d",&p[i].x,&p[i].y);	//存放N个岛的坐标
		}
		for(int i=1;i<N;i++)
		{
			for(int j=i+1;j<=N;j++)
			{
				double temp=dis(i,j);	//计算两个岛之间的距离
				if(temp>=10 && temp<=1000)	//两个岛之间的距离是合法的
				{
					e[tt].from=i;
					e[tt].to=j;
					e[tt++].cost=temp;
				}
			}
		}
		sort(e,e+tt);
		for(int i=0;i<tt;i++)
		{
			if(k==N-1)	break;	//N个点至少需要N-1条边才能保证连通
			int fafrom=findfa(e[i].from);
			int fato=findfa(e[i].to);
			if(fafrom!=fato)
			{
				merge(e[i].from,e[i].to);
				sum+=e[i].cost;	//更新最小生成树上边权之和 
				k++;	//已连接边数增加
			}
		}
		if(k==N-1)	printf("%.1lf\n",sum*100);	//可以连通的话,长度乘上单位长度的价格就是总价格了
		else	printf("oh!\n");	//不能连通
	}
	return 0;
}

---

H - Constructing Roads (HDU-1102)

There are N villages, which are numbered from 1 to N, and you should build some roads such that every two villages can connect to each other. We say two village A and B are connected, if and only if there is a road between A and B, or there exists a village C such that there is a road between A and C, and C and B are connected.
We know that there are already some roads between some villages and your job is the build some roads such that all the villages are connect and the length of all the roads built is minimum.
Input
The first line is an integer N (3 <= N <= 100), which is the number of villages. Then come N lines, the i-th of which contains N integers, and the j-th of these N integers is the distance (the distance should be an integer within [1, 1000]) between village i and village j.
Then there is an integer Q (0 <= Q <= N $\ast$ (N + 1) / 2). Then come Q lines, each line contains two integers a and b (1 <= a < b <= N), which means the road between village a and village b has been built.
Output
You should output a line contains an integer, which is the length of all the roads to be built such that all the villages are connected, and this value is minimum.

Sample Input	Sample Output
3 0 990 692 990 0 179 692 179 0 1 1 2	179

分析

注意是多组测试输入！

有 $N$ 个点（编号 $\in [1,N]$ ），给出每两个城市之间的距离。又给出 $Q$ 条路，每条路包含两个整数 $a$ 和 $b$ ，说明点 $a$ 和点 $b$ 之间的路已经修好了（不用计算这两点的路）。问你还需要多少长的路径，才能让所有的点都连通。

其实还是最小生成树的长度问题，只不过这里已经有的路，直接把他们的距离弄成 $0$ 就可以了。

代码

#include
#include
using namespace std;
typedef long long ll;
const ll maxn=110;

int N,Q,tt,sum,u,v,G[maxn][maxn];
int fa[maxn];

struct node	//结构体存边
{
	int from,to,dist;
	bool operator < (const node & other) const
	{
		return dist<other.dist; 
	}
}e[maxn*maxn];

int findfa(int x)	//寻找父亲节点
{
	if(fa[x]!=x)	return fa[x]=findfa(fa[x]);
	return fa[x];
}

void merge(int x,int y)	//合并
{
	x=findfa(x);
	y=findfa(y);
	fa[y]=x;	//更新父亲节点
}

int main()
{
	while(~scanf("%d",&N))
	{
		for(int i=1;i<=N;i++)	//初始化父亲节点
			fa[i]=i;
		tt=sum=0;
		for(int i=1;i<=N;i++)
		{
			for(int j=1;j<=N;j++)
			{
				scanf("%d",&G[i][j]);
			}
		}
		scanf("%d",&Q);
		while(Q--)
		{
			scanf("%d%d",&u,&v);
			G[u][v]=G[v][u]=0;
		}
		for(int i=1;i<N;i++)
		{
			for(int j=i+1;j<=N;j++)
			{
				e[tt].from=i;
				e[tt].to=j;
				e[tt++].dist=G[i][j];
			}
		}
		sort(e,e+tt);
		for(int i=0;i<tt;i++)
		{
			int fafrom=findfa(e[i].from);
			int fato=findfa(e[i].to);
			if(fafrom!=fato)
			{
				merge(e[i].from,e[i].to);
				sum+=e[i].dist;	//更新最小生成树上边权之和 
			}
		}
		printf("%d\n",sum);
	}
	return 0;
}

---

I - How Many Tables (HDU-1213)

Today is Ignatius’ birthday. He invites a lot of friends. Now it’s dinner time. Ignatius wants to know how many tables he needs at least. You have to notice that not all the friends know each other, and all the friends do not want to stay with strangers.
One important rule for this problem is that if I tell you A knows B, and B knows C, that means A, B, C know each other, so they can stay in one table.
For example: If I tell you A knows B, B knows C, and D knows E, so A, B, C can stay in one table, and D, E have to stay in the other one. So Ignatius needs 2 tables at least.
Input
The input starts with an integer T(1<=T<=25) which indicate the number of test cases. Then T test cases follow. Each test case starts with two integers N and M(1<=N,M<=1000). N indicates the number of friends, the friends are marked from 1 to N. Then M lines follow. Each line consists of two integers A and B(A!=B), that means friend A and friend B know each other. There will be a blank line between two cases.
Output
For each test case, just output how many tables Ignatius needs at least. Do NOT print any blanks.

Sample Input	Sample Output
2 5 3 1 2 2 3 4 5 5 1 2 5	2 4

分析

有 $T$ 组输入。每组输入给你 $N$ 个点 和 $M$ 条关系，有关系的两个点在同一个集合（ $A$ 和 $B$ 有关系， $B$ 和 $C$ 有关系，那么 $A$ 和 $C$ 也有关系）。问你共需要几个集合。

这题就需要用并查集。把有关系的点都归为同一个父亲点上，最后只需要统计它的父亲就是它自己的点的个数有几个，就说明需要几个集合。

代码

#include
typedef long long ll;
const ll maxn=1010;

int T,N,M,sum,u,v;
int fa[maxn];

int findfa(int x)	//寻找父亲节点
{
	if(fa[x]!=x)	return fa[x]=findfa(fa[x]);
	return fa[x];
}

void merge(int x,int y)	//合并
{
	x=findfa(x);
	y=findfa(y);
	fa[y]=x;	//更新父亲节点
}

int main()
{
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d%d",&N,&M);
		for(int i=1;i<=N;i++)	//初始化父亲节点
			fa[i]=i;
		sum=0;
		for(int i=1;i<=M;i++)
		{
			scanf("%d%d",&u,&v);
			merge(u,v);
		}
		for(int i=1;i<=N;i++)
		{
			if(findfa(i)==i)
			{
				sum++;
			}
		}
		printf("%d\n",sum);
	}
	return 0;
}