LeetCode题解——数组、链表、跳表
如有问题,敬请指正!
最近做的一些LeetCode题目的解答,参考了题解部分内容。
283.移动零
1. 解法一
class Solution {
// 将非零元素全部移动到前面,后面直接用0来填充
public void moveZeroes(int[] nums) {
if (nums == null || nums.length == 0) return;
int insertPos = 0;
for (int num : nums) {
if (num != 0) nums[insertPos ++] = num;
}
while (insertPos < nums.length) {
nums[insertPos ++] = 0;
}
}
}
2.解法二
class Solution {
// 记录第一个0出现的位置,然后和后面不是0的元素进行交换位置
public void moveZeroes(int[] nums) {
int k = 0;
for (int i = 0;i < nums.length;i ++) {
if (nums[i] != 0) {
swap(nums, i, k ++);
}
}
}
private void swap(int[] arr, int i, int j) {
if (i == j) return;
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
70.爬楼梯
1.解法一:记忆化递归、剪枝
class Solution {
private int[] memo; // 初始化一个记忆数组
public int climbStairs(int n) {
// 使用记忆化递归方法
if (n <= 1) return 1;
memo = new int[n + 1];
memo[0] = 1;
memo[1] = 1;
int res = helper(n);
return res;
}
private int helper(int n) {
if (n <= 1) return memo[n];
// 如果这个数出现过,就直接返回值;否则记录下来,然后递归操作
if (memo[n] != 0)
return memo[n];
else {
memo[n] = helper(n - 1) + helper(n - 2);
return memo[n];
}
}
}
2.解法二:动态规划
class Solution {
// 动态规划,自底向上递推
public int climbStairs(int n) {
if (n <= 1) return 1;
int[] memo = new int[n + 1];
memo[0] = 1;
memo[1] = 1;
for (int i = 2;i <= n;i ++) {
// 递归公式
memo[i] = memo[i - 1] + memo[i - 2];
}
return memo[n];
}
}
11.盛最多水的容器
1.解法一
class Solution {
public int maxArea(int[] height) {
if (height == null || height.length == 0) return 0;
// 设计两个指针,一前一后
int i = 0, j = height.length - 1;
int res = 0;
int area = 0;
while (i < j) {
area = Math.min(height[i], height[j]) * (j - i);
res = Math.max(res, area);
// 只有往大的一边移动才可能出现更大的面积
if (height[i] < height[j]) {
i ++;
} else {
j --;
}
}
return res;
}
}
15.三数之和
1.解法一
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
if (nums == null || nums.length < 3)
return res;
// 需要先对数组进行排序
Arrays.sort(nums);
for (int i = 0;i < nums.length - 2; i ++) {
// 如果最小的数大于0,则直接跳出,不可能得到结果为0了
if (nums[i] > 0) break;
if (i > 0 && nums[i] == nums[i - 1]) continue;
int L = i + 1, R = nums.length - 1;
while (L < R) {
int sum = nums[i] + nums[L] + nums[R];
if (sum == 0) {
res.add(Arrays.asList(nums[i], nums[L], nums[R]));
// 去重
while (L < R && nums[L] == nums[L + 1]) L ++;
while (L < R && nums[R] == nums[R - 1]) R --;
// 还需要再跳一步
L ++;
R --;
} else if (sum < 0) {
// 结果不够大
L ++;
} else {
// 结果不够小
R --;
}
}
}
return res;
}
}
2.解法二
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
if (nums == null || nums.length < 3)
return res;
// 需要先对数组进行排序
Arrays.sort(nums);
for (int i = 0;i < nums.length - 2;i ++) {
// 对第一个元素进行去重
if (i == 0 || (i > 0 && nums[i] != nums[i - 1])) {
int L = i + 1, R = nums.length - 1;
// 避免解法一中每一次while循环都新建一个目标数
int target = 0 - nums[i];
while (L < R) {
if (target == nums[L] + nums[R]) {
res.add(Arrays.asList(nums[i], nums[L], nums[R]));
while (L < R && nums[L] == nums[L + 1]) L ++;
while (L < R && nums[R] == nums[R - 1]) R --;
L ++;
R --;
} else if (target < nums[L] + nums[R]) {
R --;
} else {
L ++;
}
}
}
}
return res;
}
}
206.反转链表(背住)
1.解法一:迭代
class Solution {
public ListNode reverseList(ListNode head) {
// 记录前一个节点
ListNode prev = null;
// 当前节点
ListNode curr = head;
while (curr != null) {
// 因为要往后遍历,所以要记录一下当前节点的下一个节点
ListNode next = curr.next;
curr.next = prev;
prev = curr;
curr = next;
}
return prev;
}
}
2.解法二:递归
class Solution {
public ListNode reverseList(ListNode head) {
// 递归终止条件
if (head == null || head.next == null) return head;
ListNode prev = reverseList(head.next);
head.next.next = head;
head.next = null; // 自身顺序指向下一个节点置为空
return prev;
}
}
24.两两交换链表中的节点
1.解法一:迭代法
class Solution {
public ListNode swapPairs(ListNode head) {
if (head == null || head.next == null) return head;
ListNode dummy = new ListNode(-1);
dummy.next = head;
ListNode prev = dummy;
while (head != null && head.next != null) {
prev.next = head.next;
head.next = head.next.next;
prev.next.next = head;
prev = prev.next.next;
head = head.next;
}
return dummy.next;
}
}
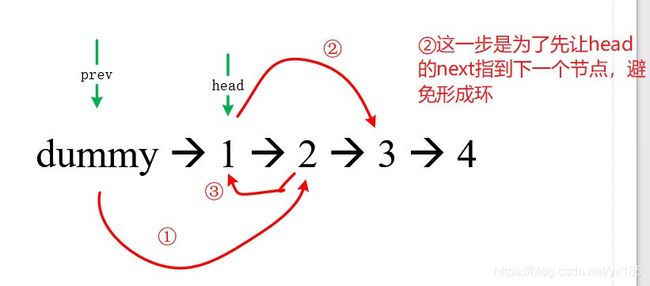
1.画图解:
2.解法二:递归
class Solution {
public ListNode swapPairs(ListNode head) {
// 递归终止条件
if (head == null || head.next == null) return head;
ListNode next = head.next;
head.next = swapPairs(next.next);
next.next = head;
return next;
}
}
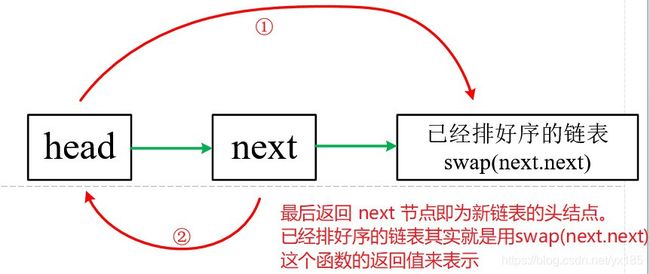
1.画图解:
- 递归就是将大问题分解为小问题,在这里就是假设现在只有三部分了,将这三部分重新排序就可以得到新的逆序链表
141.环形链表
1.解法一:快慢指针
如果在链表中存在环,慢指针一次走一步,快指针一次走两步,快指针总会追上慢指针。
public class Solution {
// 使用快慢指针
public boolean hasCycle(ListNode head) {
if (head == null || head.next == null) return false;
ListNode slow = head;
ListNode fast = head.next;
while (fast != null) {
if (slow.val == fast.val) {
return true;
}
slow = slow.next;
// 这个地方容易出现空指针异常
if (fast.next != null)
fast = fast.next.next;
else
return false;
}
return false;
}
}
// 下面的双指针更加简洁
public class Solution {
// 使用快慢指针
public boolean hasCycle(ListNode head) {
if (head == null || head.next == null) return false;
ListNode slow = head;
ListNode fast = head.next;
while (slow != fast) {
if (fast == null || fast.next == null) {
return false;
}
slow = slow.next;
fast = fast.next.next;
}
return true;
}
}
// 简洁
public class Solution {
public boolean hasCycle(ListNode head) {
if (head == null) return false;
ListNode slow = head;
ListNode fast = head;
while (fast.next != null && fast.next.next != null) {
slow = slow.next;
fast = fast.next.next;
if (slow == fast) return true;
}
return false;
}
}
- 在第13行进行的判断是因为,快指针一次走两步,如果不先判断
fast.next是否为空,就直接进行fast.next.next操作,可能就会出现null.next即空指针异常; - 加一个判断,如果出现
fast.next == null的情况,说明链表已经遍历完了,还没有发现环,则说明这个链表没有环。
1.时间复杂度:O(n)
2.空间复杂度:O(1)
2.解法二:哈希表
- 使用一个 HashSet 来存储遍历过的头结点 head,如果这个头结点已经计算过,说明存在环
- 时间空间复杂度都为 O(n),但是在
LeetCode中效率远低于快慢指针
public class Solution {
public boolean hasCycle(ListNode head) {
Set<ListNode> nodeSet = new HashSet<>();
while (head != null) {
if (nodeSet.contains(head)) {
return true;
} else {
nodeSet.add(head);
head = head.next;
}
}
return false;
}
}
142.环形链表2
1. 解法一:哈希表
public class Solution {
public ListNode detectCycle(ListNode head) {
if (head == null || head.next == null) return null;
Set<ListNode> set = new HashSet<>();
while (head != null) {
// 判断一下这个头结点出现过没有,如果出现过,则环肯定是在这个位置环上的
if (set.contains(head)) {
return head;
}
// 将遍历过的头结点放入一个set集合
set.add(head);
head = head.next;
}
return null;
}
}
2.解法二:Floyd算法
public class Solution {
public ListNode detectCycle(ListNode head) {
if (head == null || head.next == null) return null;
// 首先判断有没有环,有环的话记录一下快慢指针第一次相遇的节点
ListNode slow = head;
ListNode fast = head;
ListNode meet = null;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
if (slow == fast) {
meet = fast;
break;
}
}
// 这个条件判断是否有环,如果没有环就返回空
if (meet == null) {
return null;
}
// 有环就要进入下一步
ListNode ptr1 = head;
while (ptr1 != meet) {
ptr1 = ptr1.next;
meet = meet.next;
}
return meet;
}
}
1.时间复杂度 O(n),因为引入常数个数指针,所以空间复杂度 O(1)
2.分析
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-e4Fzlq8l-1580651913729)(F:\Java视频\极客时间-算法训练营\题解\pic\142-2.jpg)]
-
首先慢指针一次移动一步,快指针一次移动两步;
-
如果有环,两个指针第一次相遇于点 h
-
此时可以得到如下公式
2 * Distance(slow) = Distance(fast) 2 * (F + a) = F + a + b + a F = b -
所以,从第一次相遇的点 h 和头结点开始,一次移动一个位置,两个指针会在环的入口处相遇
25.K个一组翻转链表
1.解法一
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
if (k == 1) return head;
ListNode dummy = new ListNode(-1);
dummy.next = head;
ListNode prev = dummy, end = dummy;
while (end.next != null) {
for (int i = 0;i < k && end != null;i ++) end = end.next;
if (end == null) break;
ListNode start = prev.next;
ListNode next = end.next;
end.next = null; // 将前面链表和后面链表断开,next当成一个新的链表头
prev.next = reverse(start);
start.next = next;
// 更新 prev和start,开始下一次翻转
prev = start;
end = prev;
}
return dummy.next;
}
// 翻转一个链表,返回这个链表的链表头
private ListNode reverse(ListNode head) {
ListNode prev = null;
ListNode curr = head;
while (curr != null) {
ListNode next = curr.next;
curr.next = prev;
prev = curr;
curr = next;
}
return prev;
}
}
26.删除排序数组中的重复项
1.解法一:双指针
class Solution {
public int removeDuplicates(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int i = 0;
for (int j = 1;j < nums.length;j ++) {
// 用不重复的项去覆盖第一个重复的项
if (nums[j] != nums[i]) {
i ++;
nums[i] = nums[j];
}
}
return i + 1;
}
}
2.解法二
class Solution {
public int removeDuplicates(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int count = 0; // count 记录的是在当前索引指向的位置之前有多少个重复的元素,所有重复的元素
for (int i = 1;i < nums.length;i ++) {
if (nums[i] == nums[i - 1]) count ++;
else nums[i - count] = nums[i];
}
return nums.length - count;
}
}
189.旋转数组
1.解法一
时间复杂度和空间复杂度都为 O(n),且没有达到题目要求的原地算法。就是单纯的重新新建一个数组进行辅助
class Solution {
public void rotate(int[] nums, int k) {
// 最笨的方法
if (nums == null || nums.length <= 1) return;
k = k % nums.length;
int[] aux = new int[nums.length];
for (int i = 0;i < nums.length;i ++) {
aux[ (i+k) % nums.length ] = nums[i];
}
for (int i = 0;i < aux.length;i ++) {
nums[i] = aux[i];
}
}
}
2.解法二:使用反转
-
这个方法基于事实:当我们旋转一个数组 k 次, k % n 个尾部元素会被移动到头部,剩下的元素会被向后移动。在这个方法中,我们首先将所有元素反转。然后反转前 k 个元素,再反转后面 n-kn−k 个元素,就能得到想要的结果。
假设 n = 7, k = 3
原始数组 : 1 2 3 4 5 6 7 反转所有数字后 : 7 6 5 4 3 2 1 反转前 k 个数字后 : 5 6 7 4 3 2 1 反转后 n-k 个数字后 : 5 6 7 1 2 3 4 --> 结果
class Solution {
public void rotate(int[] nums, int k) {
int L = nums.length;
if (nums == null || L <= 1) return;
k = k % L;
reverse(nums, 0, L - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, L - 1);
}
private void reverse(int[] nums, int start, int end) {
while (start < end) {
int tmp = nums[start];
nums[start] = nums[end];
nums[end] = tmp;
end --;
start ++;
}
}
}
3.解法三:环状数组(未做)
- 将数组元素直接放在他的最终的位置上,但这会导致放的位置的老元素被覆盖,所以需要处理的就是保存这个老元素,将这个老元素放在他该在的位置上。
21.合并两个有序链表
1.解法一:双指针,其实也是一种归并的思想,不容易造成栈溢出
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode dummy = new ListNode(-1);
ListNode prev = dummy;
while (l1 != null && l2 != null) {
if (l1.val < l2.val) {
prev.next = l1;
l1 = l1.next;
} else {
prev.next = l2;
l2 = l2.next;
}
// 将每一个节点连接起来
prev = prev.next;
}
// 确保两个链表都被遍历完了,可以进行优化
while (l1 != null) {
prev.next = l1;
l1 = l1.next;
prev = prev.next;
}
while (l2 != null) {
prev.next = l2;
l2 = l2.next;
prev = prev.next;
}
return dummy.next;
}
}
2.对解法一后半部分的优化
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode dummy = new ListNode(-1);
ListNode prev = dummy;
while (l1 != null && l2 != null) {
if (l1.val < l2.val) {
prev.next = l1;
l1 = l1.next;
} else {
prev.next = l2;
l2 = l2.next;
}
prev = prev.next;
}
// 如果 l1 短,则返回l2
// 如果 l1 不短(要么长,要么相等),则返回 l1 就行
prev.next = l1 == null ? l2 : l1;
return dummy.next;
}
}
3.解法三:递归
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
// 递归终止条件
if (l1 == null) {
return l2;
// 递归终止条件
} else if (l2 == null) {
return l1;
// 如果两个都不为空,就可以判断l1的下一个节点了
// l1的下一个节点其实就是l1.next和l2合并之后返回的头结点
// 连接好后就可以返回l1了
} else if (l1.val < l2.val) {
l1.next = mergeTwoLists(l1.next, l2);
return l1;
// 同上
} else {
l2.next = mergeTwoLists(l1, l2.next);
return l2;
}
}
}
88.合并两个有序数组
1.解法一
1.时间复杂度O(m + n)
2.空间复杂度O(nums1.length)
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
// 还是使用两个指针来完成
// 先使用额外空间
int[] aux = new int[nums1.length];
int p1 = 0, p2 = 0, count = 0;
while (p1 < m && p2 < n) {
// if (nums1[p1] <= nums2[p2]) {
// aux[count ++] = nums1[p1];
// p1 ++;
// } else {
// aux[count ++] = nums2[p2];
// p2 ++;
// }
aux[count ++] = (nums1[p1] < nums2[p2]) ? aux[count ++] = nums1[p1 ++] : aux[count ++] = nums2[p2 ++];
}
while (p1 < m) {
aux[count ++] = nums1[p1 ++];
}
while (p2 < n) {
aux[count ++] = nums2[p2 ++];
}
for (int i = 0;i < aux.length;i ++) {
nums1[i] = aux[i];
}
}
}
2.解法二:从后往前遍历,优化空间复杂度为 O(1)
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
// 从后往前遍历,节省空间
int len1 = m - 1;
int len2 = n - 1;
int len = m + n - 1;
// 在可以移动的范围内把大数全部放到nums1的末尾
while (len1 >= 0 && len2 >= 0) {
nums1[len --] = nums1[len1] > nums2[len2] ? nums1[len1 --] : nums2[len2 --];
}
// 因为最后是把所有数合并到nums1中
// 为了避免nums2中还有数没有进行合并,需要把nums2中还没有合并的数拷贝到nums1中
// 比如nums1 = {4,5,6,7,0,0,0}
// nums2 = {1,2,3}
System.arraycopy(nums2, 0, nums1, 0, len2 + 1);
}
}
66.加一
1.解法一
class Solution {
public int[] plusOne(int[] digits) {
int carry = 0;
for (int i = digits.length - 1;i >= 0; i --) {
// 如果小于9,说明不会有进位
// if (digits[i] < 9) {
// digits[i] ++ ;
// return digits;
// 如果等于9,那么就有进位,再接着计算前面一位
// } else {
// digits[i] = 0;
// carry = 1;
// }
// 下面三行代码实现的也是上面注释掉的部分的功能
digits[i] ++;
digits[i] = digits[i] % 10; // 判断是否有进位
if (digits[i] != 0) return digits;
}
// 前面都没有返回的话说明全是9
int[] res = new int[digits.length + 1];
res[0] = 1;
return res;
}
}