计算机组成原理——数据的机器级表示
数据的机器级表示
|| 数制与编码
原码、补码、反码和移码。
通常将数值数据在计算机内部编码表示的数称为机器数，而机器数真正的值（即现实世界中带有正负号的数）称为机器数的真值。
-
原码
一个数的原码表示由符号位直接后跟数值位构成，因此，也称“符号-数值” （sign and magnitude）
缺点是 0 的表示不唯一，给使用带来不便。更重要的是，原码加减运算法则复杂。在进行原码加减运算过程中，要判定是否是两个异号数相加或两个同号数相减，若是，则必须判定两个数绝对值大小，根据判断结果决定结果符号，并用绝对值大的数减去绝对值小的数。所以现代计算机中不用原码来表示整数，只用定点原码小数来表示浮点数的尾数部分。
-
补码
补码可以实现加减运算的统一，用加法来实现减法运算。
正数的补码是它本身，负数的补码等于模与该负数绝对值之差。
对于任意一个数XT，【XT】补 = M + XT （mod M）
※ 真值——> 补码？
正数为本身；负数为各位取反加1；
※ 补码——>真值？
符号位为0那么真值就是其本身；符号位为1说明此数是负数，那么将数值位各位取反加1，符号位负。
※ 如何根据【Xt】补 求【-Xt】补？
（注意最小负数取负后会溢出，参考补码的表示范围就能理解这里的原因了！）
-
移码
主要用于表示浮点数的指数部分，方便对阶。
|| 整数的表示
- 无符号整数的表示
编码的所有二进位都用来表示数值 - 带符号整数的表示
补码表示；范围是 -2^(n-1) ~ 2^(n-1)-1
|| 实数的表示
计算机内部进行数据存储、运算和传送的部件位数有限，因而用定点数表示数值数据时，其表示范围很小。对n位带符号数，其表示范围为-2^(n-1) ~ 2^(n-1)-1 ，运算结果很容易溢出，此外，用定点数也无法表示大量带有小数点的实数。
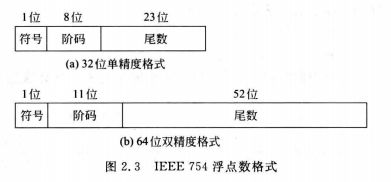
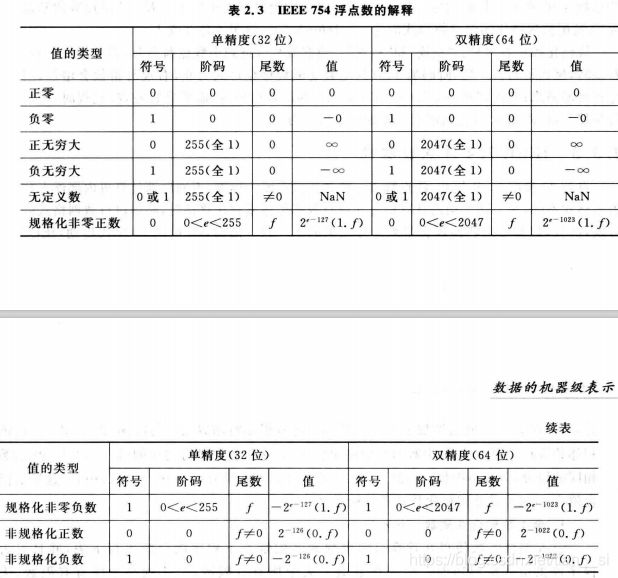
- IEEE754 （浮点数的规格化）
##############################
- 例题
############################# - IEEE754 （浮点数的具体解释）
|| 数据的宽度和存储
|| 数据校验码
数据在计算机内部进行计算、存取和传送过程中，由于元器件故障或噪音干扰等原因会出现差错。为了减少和避免这些错误，一方面要从计算机硬件本身的可靠性入手，在电路、电源、布线等各方面采取必要的措施，提高计算机的抗干扰能力；另一方面要采取相应的数据检错和校正措施，自动地发现并纠正错误。
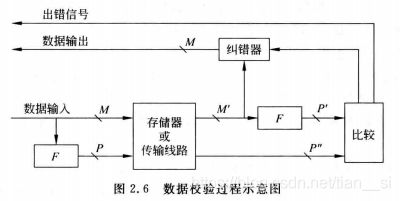
在数据校验码中，一个码字是指数据位和校验位按照某种规律排列得到的代码。将两个码字逐位比较，具有不同代码的位的个数叫做这两个码字间的距离，也成为海明距离。
-
奇偶校验码
使用步骤：
码距是2，它只能发现奇数位出错，不能发现偶数位出错，而且也不能确定发生错误的位置，不具有纠错能力。但是奇偶校验法所用的开销小，它常被用于存储器读写检查或按字节传输过程中的数据校验。因为一字节长的代码中一位出错的概率相对较大，两位以上出错则很少，所以奇偶校验码用于检验一字节长的代码还是很有效的。
-
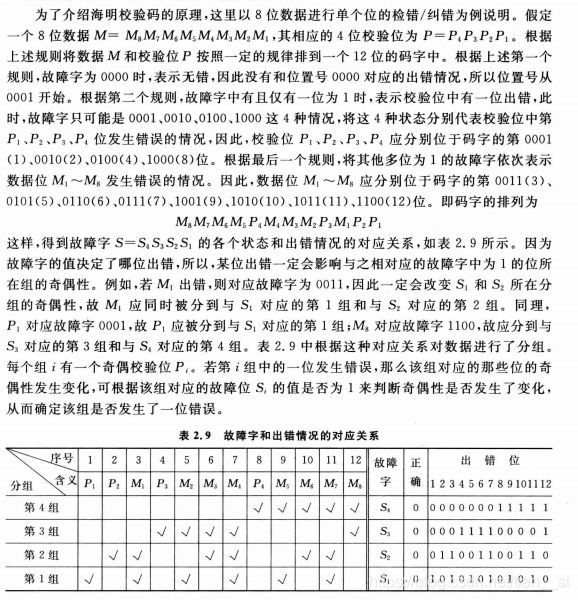
海明校验码
海明校验码实质上就是一种多重奇偶校验码。
^ 校验位的位数的确定
^ 分组方式的确定
^ 检验位的生成和检错、纠错
例：
|| 第二章作业
（更改数据：R1——0000017A R2——FFFFF895）
解：
（1）无符号
R1=（17A）H R2 = （FFFFF895）H
（2）带符号
R1 = （0000 0000 0000 0000 0000 0001 0111 1010）2
R2 = （1111 1111 1111 1111 1111 1000 1001 0101）2
可以看出R1为正数，所以真值就是他本身 （17A）H
R2为负数，现在需要把补码的形式转换为它的真值
R1 = -(0000 0000 0000 0000 0000 0111 0110 1010+1) 2 =
-(0000 0000 0000 0000 0000 0111 0110 1011)2 = -(76B）H
（3）单精度浮点数
R1 = （0 00000000 0000 0000 0000 0010 1111 010）
根据规则，阶码全0，尾数非0的是非规格化数。
0.0002F4 H * 2^(-126)
R2 = （1 11111111 11111111111100010010101）
全1阶码非0尾数 NaN
设一个变量的值为-6144 ，要求分别用32位补码整数和IEEE754单精度浮点格式表示该变量（结果用十六进制表示），并说明哪种表示其值完全正确，哪种表示是近似值？
解： （6144）10 = （0000 0000 0000 0000 0001 1000 0000 0000）2
（-6144）10= （1111 1111 1111 1111 1110 0111 1111 1111+1）=
（1111 1111 1111 1111 1110 1000 0000 0000）=（FFFFE800）H
浮点数：-1.1 * 2^12
阶码：（12+127）=（1000 1011）2
尾数1000 0000 0000 0000 0000 000
是 1100 0101 1100 0000 0000 0000 0000 0000
（C5C00000）H
32位补码形式表示完全正确，浮点数表示是近似值，因为低位被截断。
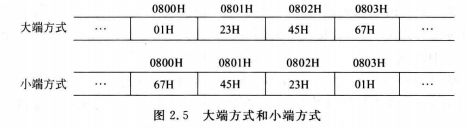
假定在一个程序中定义了变量x、y和i，其中，x和y是float型变量（用IEEE754单精度浮点数表示），i 是16位 short 型变量（用补码表示）。程序执行到某一时刻，x = -10.125 , y = 12 , i = -125 它们都被写入到了主存（按字节编址），其地址分别是 100、108 和 112。请分别画出在大端机器和小端机器上变量 x 、y 和 i 在内存的存放位置。
先处理数据：
x = -1.01001 * 2^3
阶码： （3+127） = （1000 0010）
尾数： 0100 0100 0000 0000 0000 000
符号：1
x = 1100 0001 0010 0010 0000 0000 0000 0000
（C1 22 00 00）H
y = 1.100 * 2^3
阶码： （3+127）=（1000 0010）
尾数： 1000 0000 0000 0000 0000 000
符号： 0
y = 0100 0001 0100 0000 0000 0000 0000 0000
（41 40 00 00）H
125 = （ 0000 0000 0111 1101）
-125 = （1111 1111 1000 0011）=（FF 83）H
大端方式： 小端方式：
100 C1 00
101 22 00
102 00 22
103 00 C1
108 41 00
109 40 00
110 00 40
111 00 41
112 FF 83
113 83 FF
（修改：采用偶校验码，接收校验位 1010）
解：
传输信息 ： 10001111 00111100 10101011 10010110
校验位 1010
接收信息 10000111 00111100 10101011 10010110
P^ 0010
P^^ = 1000 说明数据的第一个字节发生错误，对照传输前后，8F变成了87，说明确实发生了传输错误，验证正确。