prim算法
这几个概念清楚就别看了
完全图:任意两个顶点间都有直达的边相连的无向图。
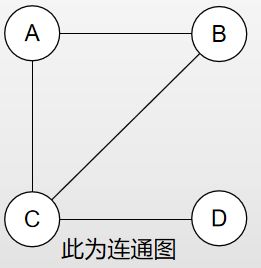
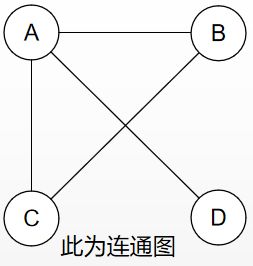
连通图:任意两个顶点间都有路径相通的无向图。
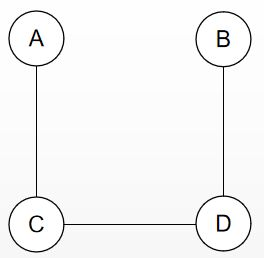
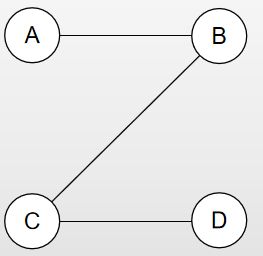
生成树:一个连通图的生成树是指一个极小连通子图,含有图中的全部n个顶点,但只有足以构成一棵树的n-1条边。
为什么是n个顶点和n-1条边呢?
我们知道树的结构,一个节点可以通过一根树支访问它的父节点,所以一个节点对应一根树枝,但树的根是没有父节点的,所以是n个节点对应n-1根树枝。若这些树枝不仅可以由子节点访问父节点,也可以由父节点访问子节点,这样的话整棵树任意两个节点都可以有路径相通,所以生成树就是一个通过顶点来确定边数使之最少的连通图。
可以发现,连通图的生成树可能并不唯一:
例:某公司想在各个办公室之间铺设通讯网络,每两个办公室之间距离不同,若想达到最低开销该怎么办?
完全图花费太大显然不行,那就先铺设代价最小的边,再铺设次之的边,直到铺完了n-1条边,过程中要保持连通且不能构成回路(有回路必定不连通),最终会确定一个花费最小的极小连通图,也就是这个连通图的最小生成树。
那么如何用算法找到这个最小生成树呢?
在上面的分析中可以发现,解决最小生成树的问题有两个:
(1):尽可能选取权值最小的边且不构成回路;
(2):选n-1条边连n个节点。
此时就说到prim算法了。这个思想还是直接用图画出来(写也写不清0.0):
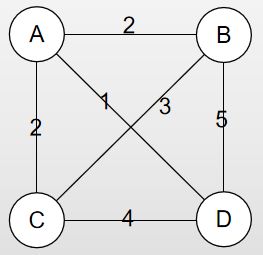
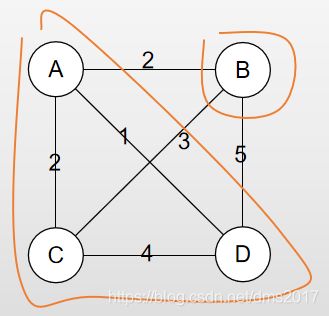
完全图是这样:
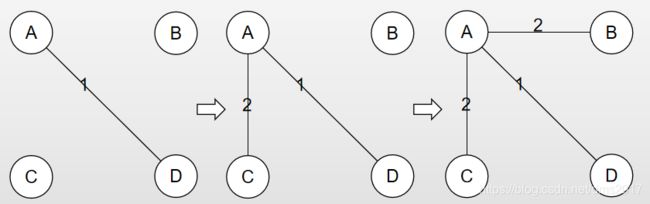
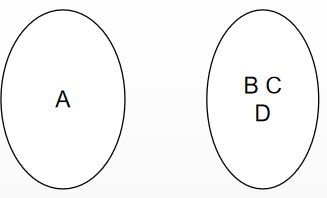
先在其中选一个顶点作为生成树的根:
此时可以将完全图看成两个图:
找到两个图之间权值最小的边(A,D),将D加入到生成树:
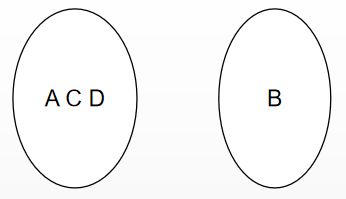
再将完全图看成两个图并找到它们之间权值最小的边(A,C)和(A,B)(随便选一个):
将C加入到生成树上,找到最小权值的边(A,B):
加入B到生成树上,此时加完了4-1=3条边得到最小生成树:
prim算法的思想是这样的,但具体怎么实现呢?
我们需要设置一个辅助对象数组closedges[],closedges[i].adjvex存储与i离得最近的节点,closedges[i].lowcost存储边(adjvex,i)的权值。
我们列表来看:
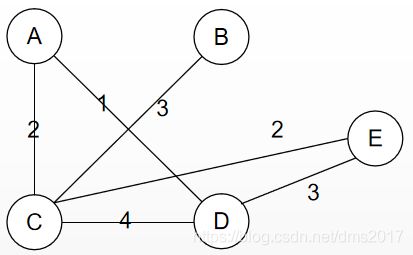
由于前面的例子太特殊,所以重新举一个例子:
| i | A | B | C | D | E | (u,v) |
| adjvex lowcost |
0 |
A
|
A 2 |
A 1 |
A
|
(A,D) |
| adjvex lowcost |
0 |
A
|
A 2 |
0 |
D 3 |
(D,C) |
| adjvex lowcost |
0 |
C 3 |
0 |
0 |
C 2 |
(C,E) |
| adjvex lowcost |
0 |
C 3 |
0 |
0 |
0 |
(C,B) |
| adjvex lowcost |
0 |
0 |
0 |
0 |
0 |
注解:第一行以A为起始点初始化closedges[],lowcost存储与A相连的顶点之间的权值,![]() 代表顶点间无路径相连,0代表此顶点已加入最小生成树,之后挑选了D作为最小生成树的第二个顶点(权值最小)。
代表顶点间无路径相连,0代表此顶点已加入最小生成树,之后挑选了D作为最小生成树的第二个顶点(权值最小)。
到第二行closedges[E]发生了变化,因为第一行选中了D作为第二个加入最小生成树的顶点,两个图之间各路径的最小权值发生了变化,所以更新数组,再次挑选两个图之间的最小权值得顶点E,之后由此类推......
存储:
图的数据结构(邻接矩阵);
class Graph {
private int vexnum ; //顶点数
private int arcnum ; //边数
private int[] vexs ; //顶点
private int[][] costs ; //邻接矩阵
private int[][] status ; //存储边的状态(1:在使用0:停用)
public Graph(int vexnum, int arcnum){ //构造方法
this.arcnum = arcnum ;
this.vexnum = vexnum ;
this.costs = new int[vexnum+1][vexnum+1] ;
this.vexs = new int[vexnum+1] ;
this.status = new int[vexnum+1][vexnum+1] ;
int i ;
for(i=1; i<=vexnum; i++){
vexs[i] = i ;
}
}
public void createGraph(){ //读入图的信息
Scanner input = new Scanner(System.in) ;
int a, b, cost, statu, i, j ;
for(i=1; i<=vexnum; i++){
for(j=1; j<=vexnum; j++){
this.costs[i][j] = Integer.MAX_VALUE ;
}
}
for(i=1; i<=this.arcnum; i++){
a = input.nextInt() ;
b = input.nextInt() ;
cost = input.nextInt() ;
this.costs[a][b] = cost ;
this.costs[b][a] = cost ;
this.status[a][b] = statu ;
}
}
public void printGraph(){ //打印图的信息
int i, j ;
for(i=1; i<=vexnum; i++){
for(j=1; j<=vexnum; j++){
System.out.printf("%11d ", costs[i][j]) ;
}
System.out.println();
}
}
public int getVexnum() {
return vexnum;
}
public int getArcnum() {
return arcnum;
}
public int getCosts(int i, int j) {
return costs[i][j];
}
}设置一个辅助对象数组closedges[],它的结构如下:
class Closedge {
private int adjvex ; //closedges[i].adjvex存储与i离得最近的节点
private int lowcost ; //closedges[i].lowcost存储边(adjvex,i)的权值
public Closedge(int adjvex, int lowcost){
this.adjvex = adjvex ;
this.lowcost = lowcost ;
}
public void setAdjvex(int adjvex) {
this.adjvex = adjvex;
}
public void setLowcost(int lowcost) {
this.lowcost = lowcost;
}
public int getAdjvex() {
return adjvex;
}
public int getLowcost() {
return lowcost;
}
}prim算法如下:思想理解后,结合前面的表格理解算法很简单,我就不再一一赘述了,代码有注释,哪里有问题随时问我,共同探讨!0.0
public static void prim(Graph g, int start){ //closeages[k].lowcost==0表示k节点已经加入到最小生成树的节点中
Closedge[] closedges = new Closedge[g.getVexnum()+1] ;
closedges[start] = new Closedge(start, 0) ;
//System.out.printf("加入的节点:%d ", start) ;
//对出发点以外的顶点初始化对应的closeages数组
int i, j, min, m = 0 ;
for(i=1; i<=g.getVexnum(); i++){
if(i != start){
closedges[i] = new Closedge(start, g.getCosts(start, i)) ;
}
}
//打印closedges
for(i=1; i<=g.getVexnum(); i++){
System.out.printf("adjvex:") ;
System.out.printf("%d ", closedges[i].getAdjvex()) ;
System.out.printf("lowcost:") ;
System.out.printf("%d ", closedges[i].getLowcost()) ;
}
System.out.println();
int sum = 0 ; //记录最小生成树的总权值
for(j=1; j<=g.getVexnum()-1; j++) {
//选择最小权的边
min = Integer.MAX_VALUE;
for (i = 1; i <= g.getVexnum(); i++) {
if (closedges[i].getLowcost() != 0 && closedges[i].getLowcost() < min) { //找出与i相关的边中的最小权值的边
m = i;
min = closedges[i].getLowcost();
}
}
sum += closedges[m].getLowcost();
closedges[m].setLowcost(0); //将m顶点加入生成树
//System.out.printf("%d ", m);
//由于新加入的m顶点导致当前生成树U与集合V-U连接的最小权值的边可能发生变化,所以更新closeages数组的值
for (i = 1; i <= g.getVexnum(); i++) {
if (i != m && g.getCosts(m, i) < closedges[i].getLowcost()) {
closedges[i].setLowcost(g.getCosts(m, i));
closedges[i].setAdjvex(m); //因为与m相连接,所以赋值m
}
}
//打印closedges数组
for(i=1; i<=g.getVexnum(); i++){
System.out.printf("adjvex:") ;
System.out.printf("%d ", closedges[i].getAdjvex()) ;
System.out.printf("lowcost:") ;
System.out.printf("%d ", closedges[i].getLowcost()) ;
}
System.out.println();
}
System.out.println();
System.out.printf("最小生成树的权值:%d", sum) ;
}
运行结果: