【数据结构】拓扑排序与关键路径求解

拓扑排序

拓扑排序是关键路径求解的前提条件，与拓扑排序相关的数据结构叫做AOV网（activity on vertex network），即活动在顶点上的网，在网中若有从顶点i出发，指向顶点j的一条边，那么称顶点i为顶点j的前驱，顶点j为顶点i的后继，作为时间来表示的话那么就表示顶点i表示的事件完成了之后才能开始顶点j的事件。

拓扑排序就是用来求解一个行之有效的工作序列的算法。

算法描述如下：

（1）随机取一个没有入度的顶点，将其和从其出发的边删除（也就是有些顶点的入度需要减一）

（2）重复（1）的步骤直到没有顶点位置，如果还有顶点有入度没有删除，那么就证明图有环，不存在拓扑序列

 

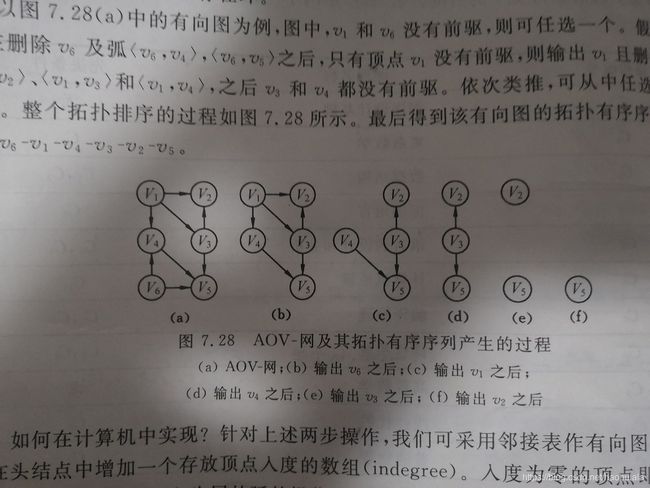
如上图是书上的一个例子

用邻接表存储的图的拓扑排序代码

//拓扑排序//
void TopologicalSort(AdjGraph *G) {
	EdgeNode *e;
	int i, k, gettop;
	int top = 0;//栈顶指针
	int count = 0;//计数器
	int *stack;
	stack = (int *)malloc(G->Vex_num * sizeof(int));//分配一个栈的内存空间
	for (i = 0; i < G->Vex_num; i++) {
		//将入度为0的结点都入栈
		if (G->adjlist[i].in == 0) {
			stack[++top] = i;//入栈
		}
	}
	printf("拓扑排序的结果为：\n");
	gettop = stack[top--];//取出栈顶元素
	printf("%d", G->adjlist[gettop].data);
	count++;//进行计数
	for (e = G->adjlist[gettop].firstedge; e; e = e->next) {
		//对该顶点弧表进行遍历减去入度
		k = e->adjvex;
		G->adjlist[k].in--;
		if (G->adjlist[k].in == 0) {
			//如果入度为0就入栈
			stack[++top] = k;
		}
	}
	while (top != 0) {
		//栈不空的话
		gettop = stack[top--];//取出栈顶元素
		printf(" -> %d", G->adjlist[gettop].data);
		count++;//进行计数
		for (e = G->adjlist[gettop].firstedge; e; e = e->next) {
			//对该顶点弧表进行遍历减去入度
			k = e->adjvex;
			G->adjlist[k].in--;
			if (G->adjlist[k].in == 0) {
				//如果入度为0就入栈
				stack[++top] = k;
			}
		}
	}
	printf("\n");
	if (count == G->Vex_num) {
		printf("该图无环路，拓扑排序完成\n");
	}
	else {
		printf("该图存在环路，拓扑排序失败\n");
	}
}

关键路径

关键路径涉及到的数据结构是AOE网（activity on edge），其中顶点表示事件，或者（表示活动的开始或者结束），边的权值为活动所需要的时间。

开始的事件为源点，其入度为0；结束的事件为汇点，其出度为0。

所谓关键路径就是指最晚开始时间和最早开始时间相等的活动所构成的一条路径。

在这里我们把路径长度定义为所经过边的权值之和。

为了求得关键路径，我们需要求4个变量，他们分别是 事件的最早开始时间ve ，事件的最晚开始时间vl 活动的最早开始时间ee 和活动的最晚开始时间el

接下里我们来介绍四个变量的值

事件最早开始时间ve：源点的ve为0，假设要求ve(j)，那么ve(j)=max{ve(i) + wij} ,其中wij为从i到j的边的权值

事件最晚开始时间vl：汇点的最晚开始时间为其ve值，那么ve(j)=min{vl(k) - wjk},其中wjk为从j到k的边的权值

活动的最早开始时间ee：对于活动ai，其边是从i指向j的一条权重为wij的边，那么ee(i)=ve(i)

活动的最晚开始时间el：对于活动aj，其边是从j指向k的一条权重为wjk的边，那么el(j)=vl(k)-wjk

一个鲜活的例子（考试应该就是这样解题了）

这个up讲的很不错的，需要视频的小伙伴可以去b站看这个up讲的课。

关键路径求解代码

同样使用的是邻接表存储的图结构

//关键路径//
int *etv, *ltv;//表示事件最早发生时间和时间最迟发生时间
int *stack2;//为最迟事件发生时间提供存储
int top2;//stack2的栈顶指针
 
//改进版的拓扑排序
void TopologiaclSortPro(AdjGraph *G) {
	EdgeNode *e;
	int i, k, gettop;
	int top = 0;
	int count = 0;
	int *stack1;//拓扑排序的栈
	stack1 = (int *)malloc(G->Vex_num * sizeof(int));
	for (i = 0; i < G->Vex_num; i++) {
		//初始化stack1堆栈
		if(G->adjlist[i].in == 0)
		stack1[++top] = i;
	}
	top2 = 0;
	etv = (int *)malloc(G->Vex_num * sizeof(int));//事件最早发生时间
	for (i = 0; i < G->Vex_num; i++) {
		etv[i] = 0;//初始化事件最早发生时间
	}
	stack2 = (int *)malloc(G->Vex_num * sizeof(int));
	printf("拓扑排序的结果为：\n");
	gettop = stack1[top--];
	count++;
	stack2[++top2] = gettop;//出栈了之后如stack2，为的是计算事件最晚开始时间
	printf(" %d", G->adjlist[gettop].data);
	for (e = G->adjlist[gettop].firstedge; e; e = e->next) {
		//这里实际上是检索所有入度为0顶点有关联的边
		k = e->adjvex;
		G->adjlist[k].in--;
		if (G->adjlist[k].in == 0) {
			//入栈
			stack1[++top] = k;
		}
		if (etv[gettop] + e->weight > etv[k]) {
			//最早开始时间应该是最大的那个路径，因为所有准备工作完成才能开始
			etv[k] = etv[gettop] + e->weight;
		}
	}
	while (top != 0) {
		//当stack1不空的时候
		gettop = stack1[top--];
		count++;
		stack2[++top2] = gettop;//出栈了之后如stack2，为的是计算事件最晚开始时间
		printf(" -> %d",G->adjlist[gettop].data);
		for (e = G->adjlist[gettop].firstedge; e; e = e->next) {
			//这里实际上是检索所有入度为0顶点有关联的边
			k = e->adjvex;
			G->adjlist[k].in--;
			if (G->adjlist[k].in == 0) {
				//入栈
				stack1[++top] = k;
			}
			if (etv[gettop] + e->weight > etv[k]) {
				//最早开始时间应该是最大的那个路径，因为所有准备工作完成才能开始
				etv[k] = etv[gettop] + e->weight;
			}
		}
	}
	if (count == G->Vex_num) {
		printf("\n没有回路，排序完成\n");
	}
	else {
		printf("\n存在回路，排序失败\n");
	}
	printf("事件最早开始时间为：\n");
	for (int i = 0; i < G->Vex_num; i++) {
		printf("V%d\t", i);
	}
	printf("\n");
	for (int i = 0; i < G->Vex_num; i++) {
		printf("%d\t", etv[i]);
	}
	printf("\n");
}
 
//关键路径
void CriticalPath(AdjGraph *G) {
	EdgeNode *e;
	int i, gettop, k, j, count = 0;
	int ete, lte;//活动最早发生时间和活动最晚发生时间
	TopologiaclSortPro(G);//排序，获得stack2堆栈
	ltv = (int *)malloc(G->Vex_num * sizeof(int));//事件最迟发生时间
	for (i = 0; i < G->Vex_num; i++) {
		//用汇点最早开始时间来初始化ltv
		ltv[i] = etv[G->Vex_num - 1];
	}
	printf("关键路径为：\n");
	while (top2 != 0) {
		//只要把stack2弹出干净就行了
		gettop = stack2[top2--];
		for (e = G->adjlist[gettop].firstedge; e; e = e->next) {
			//逐一往后退来计算事件最晚发生时间
			k = e->adjvex;
			if (ltv[k] - e->weight < ltv[gettop]) {
				//k表示从后面往前判定
				ltv[gettop] = ltv[k] - e->weight;
			}
		}
		//计算ete和lte来判断关键路径
		//这两个实际上就是边		
		for (j = 0; j < G->Vex_num; j++) {
			//从每个顶点出发
			for (e = G->adjlist[j].firstedge; e; e = e->next) {
				k = e->adjvex;
				ete = etv[j];//活动最早开始时间就是顶点的最早开始时间
				lte = ltv[k] - e->weight;
				count++;
				//如果两个相等代表这是关键路径
				if (ete == lte) {
					printf("V%d -> V%d  length：%d\n", G->adjlist[j].data, G->adjlist[k].data, e->weight);
				}
			}
		}
	}
	printf("\n");
	printf("事件最晚开始时间为：\n");
	for (int i = 0; i < G->Vex_num; i++) {
		printf("V%d\t", i);
	}
	printf("\n");
	for (int i = 0; i < G->Vex_num; i++) {
		printf("%d\t", ltv[i]);
	}
}