3D图形学基础 基本概念

转载：https://zhuanlan.zhihu.com/p/27846162

3D图形学基础

Lingtonke（柯灵杰）

 

1 前言

现在AR、VR技术正值风口，催生了一大批相关的APP，使得3D图像学不再是游戏开发人员的专属知识，而是更多的普及开来。

本文主要针对一些对3D有兴趣的同学，普及图形学知识，不涉及深入的技术探讨和样例介绍。对于不是从事相关开发的同学也能了解相关的知识

部分材料来源于网络和书籍。

2 什么是图形学

图形学也称计算机图形学（ComputerGraphics），简称CG。它是研究图形的输入、模型(图形对象)的构造和表示、图形数据库管理、图形数据通信、图形的操作、图形数据的分析，以及如何以图形信息为媒介实现人机交互作用的方法、技术和应用的一门学科。它包括图形系统硬件(图形输入-输出设备、图形工作站)图形软件、算法和应用等几个方面。

图形学的研究内容非常广泛，如图形硬件、图形标准、图形交互技术、光栅图形生成算法、曲线曲面造型、实体造型、真实感图形计算与显示算法，以及科学计算可视化、计算机动画、自然景物仿真、虚拟现实等。

平时我们开发游戏或者VR应用用到的，属于其中的一个分支：实时渲染（RealtimeRendering）

渲染（render，或称“绘制”）在电脑绘图中，是指：用软件从模型生成图像的过程。模型是用语言或者数据结构进行严格定义的三维物体或虚拟场景的描述，它包括几何、视点、纹理、照明和阴影等信息。图像是数字图像或者位图图像。渲染用于描述：计算视频编辑软件中的效果，以生成最终视频的输出过程。

渲染是三维计算机图形学中的最重要的研究课题之一，并且在实践领域它与其它技术密切相关。在图形流水线中，渲染是最后一项重要步骤，通过它得到模型与动画最终显示效果。自从二十世纪七十年代以来，随着计算机图形的不断复杂化，渲染也越来越成为一项重要的技术。

渲染的应用领域有：计算机与视频游戏、模拟、电影或者电视特效以及可视化设计，每一种应用都是特性与技术的综合考虑。作为产品来看，现在已经有各种不同的渲染工具产品，有些集成到更大的建模或者动画包中，有些是独立产品，有些是开放源代码的产品。从内部来看，渲染工具都是根据各种学科理论，经过仔细设计的程序，其中有：光学、视觉感知、数学以及软件开发。

实时渲染经常用于三维视频游戏，通常依靠图形处理器（GPU）完成这个过程。

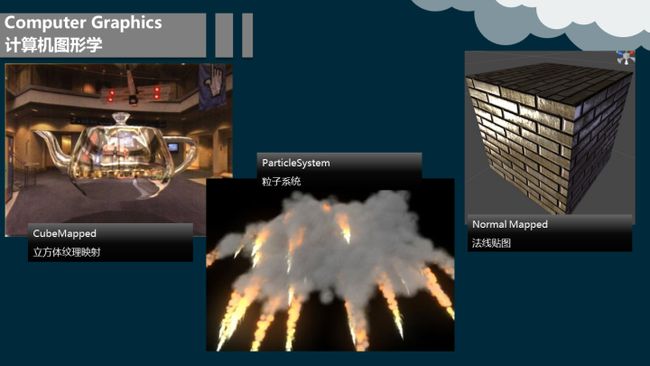
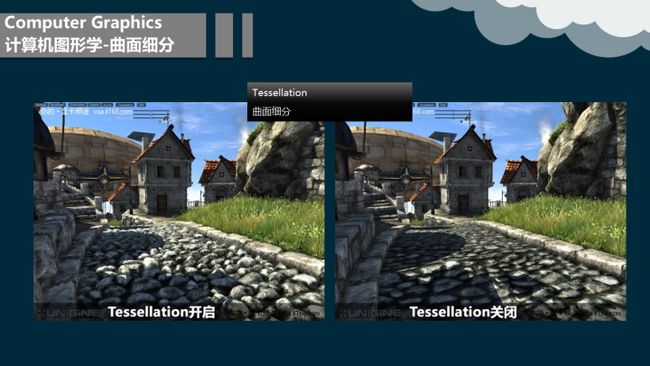
3 效果展示

 

 

 

 

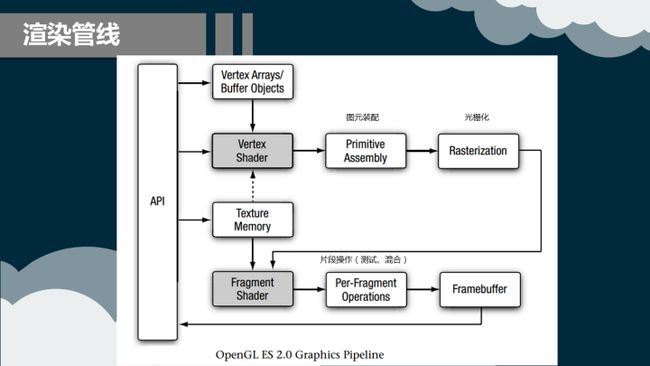
4 渲染管线

 

 

4.1 什么是渲染管线

渲染管线也称为渲染流水线或像素流水线或像素管线，是显示芯片内部处理图形信号相互独立的的并行处理单元。在某种程度上可以把渲染管线比喻为工厂里面常见的各种生产流水线，工厂里的生产流水线是为了提高产品的生产能力和效率，而渲染管线则是提高显卡的工作能力和效率。

渲染管线就是显示核心中负责给图形配上颜色的一组专门通道。它是显示核心中单独设计的一组电路，拥有单独的晶体管。渲染管线越多，那么所绘出的图形它的填充效率就越高，自然我们看到的画面也就越流畅越精美。这就是为什么渲染管线越多越好的原因。如果少了，那么自然就会使显卡的性能下降。当然渲染管线越多，显示核心就会越大，因为它所使用的晶体管数目增加了。

4.2 渲染管线的流程

4.2.1 总流程图

 

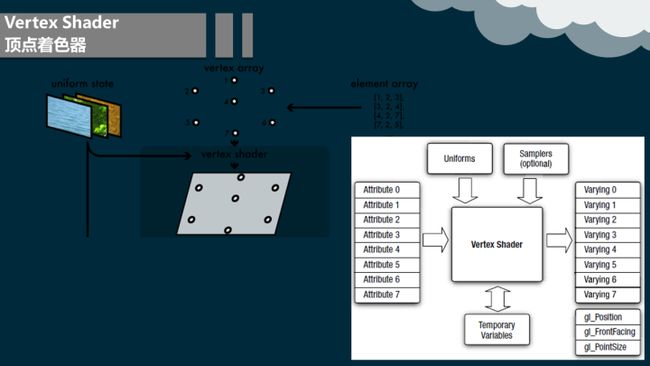
4.2.2 顶点着色器

 

 

为了实现逼真的场景，仅渲染对象的形状和位置是不足够的，它们的外观亦需要模拟。这些描述包括第每对象材质，以及光源照射对象产生的特效。模拟材质和光源的方法有很多种，包括从最简单的颜色到精细的物理特性描述。

决定光和材质特效的操作称为着色。它包括了计算不同点的着色方程。典型的某些这类的计算运行在几何阶段的模型顶点数组上，另外一些则运行在逐象素的光珊化阶段。各类的材质数据，例如点所在位置，法向量，颜色或其它着色方程需用到的数值信息，可储存在每个顶点中。顶点着色的结果（这可能是颜色，向量，纹理坐标或其它种类的着色数据）会被送进光珊化阶段去插值。

着色阶段通常被认为是发生在世界空间。在实践中，有时则将相应的实体（例如摄像机和光源）变换到其它空间（例如模型或视觉空间）并在那运行计算更为方便。因为如果所有包含在着色计算中的对象均被变换到同一空间，则光源、摄像机和模型的相对关系是保留的。

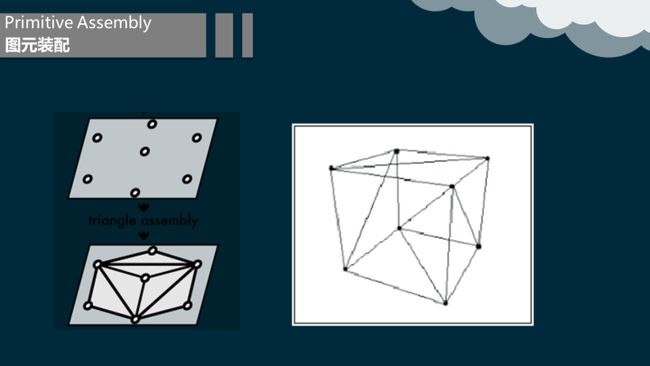
4.2.3 图元装配

 

经过变换的顶点流按照顺序被送到下一个被称为图元装配的阶段。首先，在图元装配阶段根据伴随顶点序列的几何图元分类信息把顶点装配成几何图元。这将产生一序列的三角形、线段和点。这些图元需要经过裁剪到可视平截体（三维空间中一个可见的区域）和任何有效地应用程序指定的裁剪平面。

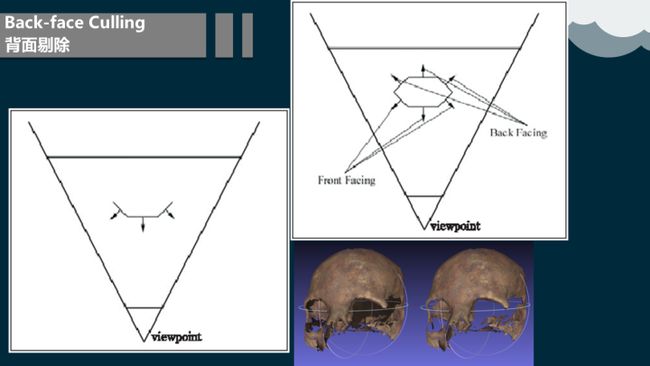
4.2.4 背面剔除

 

 

我们知道，渲染的基本单位是一个个的三角形面片。无论多么复杂的3D 模型都是由一个个基本的三角型的面片组成的。既然是一个面片，那必然就有两个面，如果其中有一个面被称为正面，那相应的另一面就被称为背面。

同一时刻我们在看见某一面的同时，另外一面则必然是看不的。在这里我们可以想象一个封闭的不透明的几何体，我们肉眼只能看到它的外面，而它的内部我们是看不见的。如果没有开启表面剔除，则可能有很多从一般常识上看来是看不见的那一面（比如几何体内部），它也会去渲染。这显然会大大降低渲染效率和增加不必要的系统开销。

渲染中通过顶点的排列顺序来决定正反面

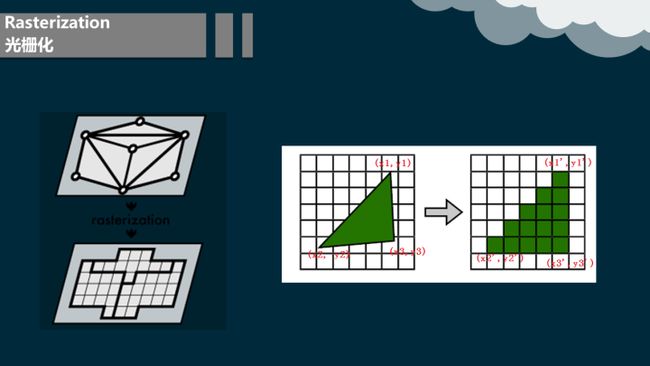
4.2.5 光栅化

 

 

得到已变换及投影后的顶点及与之相关联的着色数据，光珊阶段的目标是计算并设置像素的颜色。这个过程叫光珊化或扫描变换，即从二维顶点所处的屏幕空间（所有顶点都包含Z值即深度值，及各种与相关的着色信息）到屏幕上的像素的转换。

4.2.6 测试和混合

 

 

4.2.6.1 裁剪测试

将超出屏幕的部分裁剪掉，无需后续运算

4.2.6.2 采样

 

 

采样（sampling）又称取样，指把时间域或空间域的连续量转化成离散量的过程。

抗锯齿（英语：anti-aliasing，简称AA），也译为边缘柔化、消除混叠、抗图像折叠有损等。它是一种消除显示器输出的画面中图物边缘出现凹凸锯齿的技术，那些凹凸的锯齿通常因为高分辨率的信号以低分辨率表示或无法准确运算出3D图形坐标定位时所导致的图形混叠（aliasing）而产生的，反锯齿技术能有效地解决这些问题。它通常被用在在数字信号处理、数字摄影、电脑绘图与数码音效及电子游戏等方面，柔化被混叠的数字信号。

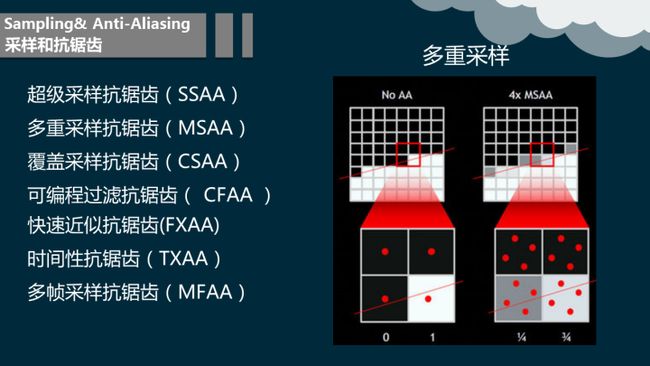
4.2.6.2.1 超级采样抗锯齿（SSAA）

超级采样抗锯齿（Super-Sampling Anti-aliasing，简称SSAA）此是早期抗锯齿方法，比较消耗资源，但简单直接，先把图像映射到缓存并把它放大，再用超级采样把放大后的图像像素进行采样，一般选取2个或4个邻近像素，把这些采样混合起来后，生成的最终像素，令每个像素拥有邻近像素的特征，像素与像素之间的过渡色彩，就变得近似，令图形的边缘色彩过渡趋于平滑。再把最终像素还原回原来大小的图像，并保存到帧缓存也就是显存中，替代原图像存储起来，最后输出到显示器，显示出一帧画面。这样就等于把一幅模糊的大图，通过细腻化后再缩小成清晰的小图。如果每帧都进行抗锯齿处理，游戏或视频中的所有画面都带有抗锯齿效果。而将图像映射到缓存并把它放大时，放大的倍数被用于分别抗锯齿的效果，如：图1，AA后面的x2、x4、x8就是原图放大的倍数。 超级采样抗锯齿中使用的采样法一般有两种：

1.顺序栅格超级采样（Ordered Grid Super-Sampling，简称OGSS），采样时选取2个邻近像素。

2.旋转栅格超级采样（Rotated Grid Super-Sampling，简称RGSS），采样时选取4个邻近像素。

4.2.6.2.2 多重采样抗锯齿（MSAA）

多重采样抗锯齿（MultiSampling Anti-Aliasing，简称MSAA）是一种特殊的超级采样抗锯齿（SSAA）。MSAA首先来自于OpenGL。具体是MSAA只对Z缓存（Z-Buffer）和模板缓存(Stencil Buffer)中的数据进行超级采样抗锯齿的处理。可以简单理解为只对多边形的边缘进行抗锯齿处理。这样的话，相比SSAA对画面中所有数据进行处理，MSAA对资源的消耗需求大大减弱，不过在画质上可能稍有不如SSAA。

4.2.6.2.3 覆盖采样抗锯齿（CSAA）

覆盖采样抗锯齿（CoverageSampling Anti-Aliasing，简称CSAA）是nVidia在G80及其衍生产品首次推向实用化的AA技术，也是目前nVidia GeForce 8/9/G200系列独享的AA技术。CSAA就是在MSAA基础上更进一步的节省显存使用量及带宽，简单说CSAA就是将边缘多边形里需要取样的子像素坐标覆盖掉，把原像素坐标强制安置在硬件和驱动程序预先算好的坐标中。这就好比取样标准统一的MSAA，能够最高效率的执行边缘取样，效能提升非常的显著。比方说16xCSAA取样性能下降幅度仅比4xMSAA略高一点，处理效果却几乎和8xMSAA一样。8xCSAA有着4xMSAA的处理效果，性能消耗却和2xMSAA相同。[1]

4.2.6.2.4 可编程过滤抗锯齿(CFAA)

可编程过滤抗锯齿（Custom Filter Anti-Aliasing）技术起源于AMD-ATI的R600家庭。简单地说CFAA就是扩大取样面积的MSAA，比方说之前的MSAA是严格选取物体边缘像素进行缩放的，而CFAA则可以通过驱动和谐灵活地选择对影响锯齿效果较大的像素进行缩放，以较少的性能牺牲换取平滑效果。显卡资源占用也比较小。

4.2.6.2.5 快速近似抗锯齿(FXAA)

快速近似抗锯齿(Fast Approximate Anti-Aliasing) 它是传统MSAA(多重采样抗锯齿)效果的一种高性能近似值。它是一种单程像素着色器，和MLAA一样运行于目标游戏渲染管线的后期处理阶段 。

4.2.6.2.6 时间性抗锯齿（TXAA）

让电影画质的游戏体验达到逼真水平。

TXAA 抗锯齿: 比 MSAA和FXAA 以及 CSAA 的画质更高，制作CG电影的电影制片厂会在抗锯齿方面花费大量的计算资源，从而可确保观众不会因不逼真的锯齿状线条而分心。如果想要让游戏接近这种级别的保真度，那么开发商需要全新的抗锯齿技术，不但要减少锯齿状的线条，而且要减少锯齿状闪烁情形，同时还不降低性能。为了便于开发商实现这种保真度的提升，英伟达设计了画质更高的抗锯齿模式，名为TXAA.该模式专为直接集成到游戏引擎中而设计。与CG电影中所采用的技术类似，TXAA集MSAA的强大功能与复杂的解析滤镜于一身，可呈现出更加平滑的图像效果，远远超越了所有同类技术。此外，TXAA还能够对帧之间的整个场景进行抖动采样，以减少闪烁情形，闪烁情形在技术上又称作时间性锯齿。目前，TXAA有两种模式：TXAA 2X和TXAA 4X。TXAA 2X可提供堪比8X MSAA的视觉保真度，然而所需性能却与2X MSAA相类似；TXAA 4X的图像保真度胜过8XMSAA，所需性能仅仅与4X MSAA相当。[2]

4.2.6.2.7 多帧采样抗锯齿（MFAA）

NVIDIA（英伟达）根据MSAA改进出的一种抗锯齿技术。目前只有使用 Maxwell 架构GPU的显卡才可以使用。在 Maxwell 上，英伟达推出了用于光栅化的可编程采样位置，它们被存储在随机存取存储器 (RAM) 中。如此一来便为更灵活、更创新的全新抗锯齿技术创造了机会，这类抗锯齿技术能够独特地解决现代游戏引擎所带来的难题，例如高画质抗锯齿对性能的更高要求。只要在NVIDIA控制面板里为程序开启MFAA并在游戏中选择MSAA就可以开启。画面表现明显强于同级别的MSAA，这种全新抗锯齿技术在提升边缘画质的同时能够将性能代价降至最低。通过在时间和空间两方面交替使用抗锯齿采样格式，4xMFAA 的性能代价仅相当于 2xMSAA，但是抗锯齿效果却与 4xMSAA相当。

4.2.6.3 模板测试

 

 

模板测试是所有测试中比较复杂的一种

在模板缓冲区中为每个像素保存了一个“模板值”，当像素需要进行模板测试时，将设定的模板参考值与该像素的“模板值”进行比较，符合条件的通过测试，不符合条件的则被丢弃，不进行绘制。

条件的设置与Alpha测试中的条件设置相似。但注意Alpha测试中是用浮点数来进行比较，而模板测试则是用整数来进行比较。比较也有八种情况：始终通过、始终不通过、大于则通过、小于则通过、大于等于则通过、小于等于则通过、等于则通过、不等于则通过。

4.2.6.4 深度测试

 

 

4.2.6.5 什么是深度？

深度其实就是该象素点在3d世界中距离摄象机的距离（绘制坐标），深度缓存中存储着每个象素点（绘制在屏幕上的）的深度值！

深度值（Z值）越大，则离摄像机越远。

深度值是存贮在深度缓存里面的，我们用深度缓存的位数来衡量深度缓存的精度。深度缓存位数越高，则精确度越高，目前的显卡一般都可支持16位的Z Buffer，一些高级的显卡已经可以支持32位的Z Buffer，但一般用24位Z Buffer就已经足够了。

4.2.6.6 为什么需要深度？

在不使用深度测试的时候，如果我们先绘制一个距离较近的物体，再绘制距离较远的物体，则距离远的物体因为后绘制，会把距离近的物体覆盖掉，这样的效果并不是我们所希望的。而有了深度缓冲以后，绘制物体的顺序就不那么重要了，都能按照远近（Z值）正常显示，这很关键。

实际上，只要存在深度缓冲区，无论是否启用深度测试，在像素被绘制时都会尝试将深度数据写入到缓冲区内。这些深度数据除了用于常规的测试外，还可以有一些有趣的用途，比如绘制阴影等等。

4.2.7 混合

 

 

“混合”是指两种颜色的叠加方式。在新图片将要渲染画到屏幕上的时候，将用在新图片中的红、绿、蓝和透明度信息，与屏幕上已经存在的图片颜色信息相融合。

说的具体一点，就是把某一像素位置上原来的颜色和将要画上去的颜色，通过某种方式混在一起，从而实现特殊的效果。

把源颜色和目标颜色各自取出，并乘以一个系数（源颜色乘以的系数称为“源因子”，目标颜色乘以的系数称为“目标因子”），然后相加，这样就得到了新的颜色。

4.2.8 抖动

 

 

4.2.8.1 什么是抖动

对于可用颜色较少的系统，可以以牺牲分辨率为代价，通过颜色值的抖动来增加可用颜色数量。抖动操作是和硬件相关的，允许程序员所做的操作就只有打开或关闭抖动操作。实际上，若机器的分辨率已经相当高，激活抖动操作根本就没有任何意义。默认情况下，抖动是激活的。

4.2.8.2 如何抖动

图案化使用图案来表示象素的灰度，那么我们来做一道计算题。假设有一幅240×180×8bit的灰度图，当用分辨率为300dpi×300dpi的激光打印机将其打印到12.8×9.6英寸的纸上时，每个象素的图案有多大？

这道题很简单，这张纸最多可以打(300×12.8) ×(300×9.6)=3840×2880个点，所以每个象素可以用(3840/240)×(2880/180)=16×16个点大小的图案来表示，即一个象素256个点。如果这16×16的方块中一个黑点也没有，就可以表示灰度256；有一个黑点，就表示灰度255；依次类推，当都是黑点时，表示灰度0。这样，16×16的方块可以表示257级灰度，比要求的8bit共256级灰度还多了一个。所以上面的那幅图的灰度级别完全能够打印出来。

这里有一个图案构成的问题，即黑点打在哪里？比如说，只有一个黑点时，我们可以打在正中央，也可以打16×16的左上角。图案可以是规则的，也可以是不规则的。一般情况下，有规则的图案比随即图案能够避免点的丛集，但有时会导致图象中有明显的线条。

如下图所示，2×2的图案可以表示5级灰度，

 

 

当图象中有一片灰度为的1的区域时，如下所示，有明显的水平和垂直线条。

 

 

如果想存储256级灰度的图案，就需要256×16×16的二值点阵，占用的空间还是相当可观的。有一个更好的办法是：只存储一个整数矩阵，称为标准图案，其中的每个值从0到255。图象的实际灰度和阵列中的每个值比较，当该值大于等于灰度时，对应点打一黑点。下面举一个25级灰度的例子加以说明。

 

 

上图，左边为标准图案，右边为灰度为15的图案，共有10个黑点，15个白点。其实道理很简单，灰度为0时全是黑点，灰度每增加1，减少一个黑点。要注意的是，5×5的图案可以表示26种灰度，当灰度是25才是全白点，而不是灰度为24时。

下面介绍一种设计标准图案的算法，是由Limb在1969年提出的。

先以一个2×2的矩阵开始：设

 

 

通过递归关系有：

 

 

其中Mn和Un均为2n×2n的方阵，Un的所有元素都是1。根据这个算法，可以得到

 

 

为16级灰度的标准图案。

M3(8×8阵)比较特殊，称为Bayer抖动表。M4是一个16×16的矩阵。

根据上面的算法，如果利用M3一个象素要用8×8的图案表示，则一幅N×N的图将变成8N×8N大小。如果利用M4，就更不得了，变成16N×16N了。能不能在保持原图大小的情况下利用图案化技术呢？一种很自然的想法是：如果用M2阵，则将原图中每8×8个点中取一点，即重新采样，然后再应用图案化技术，就能够保持原图大

小。实际上，这种方法并不可行。首先，你不知道这8×8个点中找哪一点比较合适，另外，8×8的间隔实在太大了，生成的图象和原图肯定相差很大，就象下图最右边的那幅图一样。

 

 

我们可以采用这样的做法：假设原图是256级灰度，利用Bayer抖动表，做如下处理

if (g[y][x]>>2) > bayer[y&7][x&7] then 打一白点 else 打一黑点

其中，x,y代表原图的象素坐标，g[y][x]代表该点灰度。首先将灰度右移两位，变成64级，然后将x，y做模8运算，找到Bayer表中的对应点，两者做比较，根据上面给出的判据做处理。

我们可以看到，模8运算使得原图分成了一个个8×8的小块，每个小块和8×8的Bayer表相对应。小块中的每个点都参与了比较，这样就避免了上面提到的选点和块划分过大的问题。

 

 

5 坐标变换

 

 

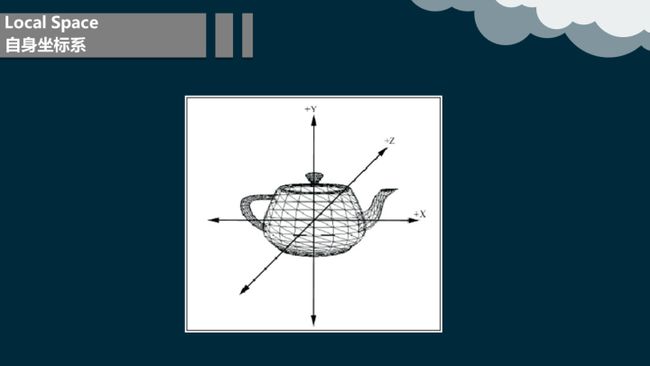
5.1 自身坐标系

 

 

自身坐标系又叫做建模空间，这是我们定义物体的三角形列的坐标系。自身坐标系简化了建模的过程。在物体自己的坐标系中建模比在世界坐标系中直接建模更容易。例如，在自身坐标系中建模不像在世界坐标系中要考虑本物体相对于其他物体的位置、大小、方向关系。

 

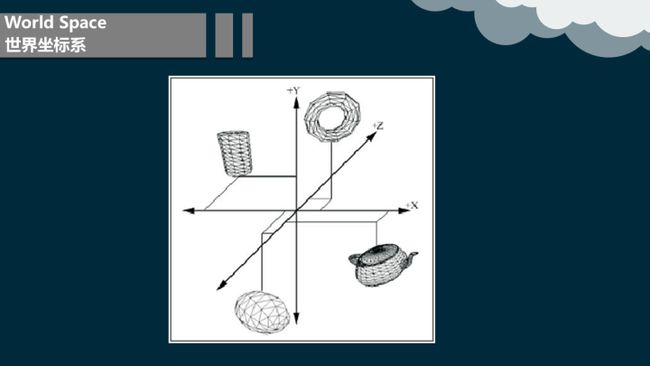
5.2 世界坐标系

 

 

一旦我们构造了各种模型，它们都在自己的自身坐标系中，但是我们需要把它们都放到同一个世界坐标系中。物体从自身坐标系到世界坐标系中的换叫做世界变换。世界变换通常是用平移、旋转、缩放操作来设置模型在世界坐标系中的位置、大小、方向。世界变换就是通过各物体在世界坐标系中的位置、大小和方向等相互之间的关系来建立所有物体。

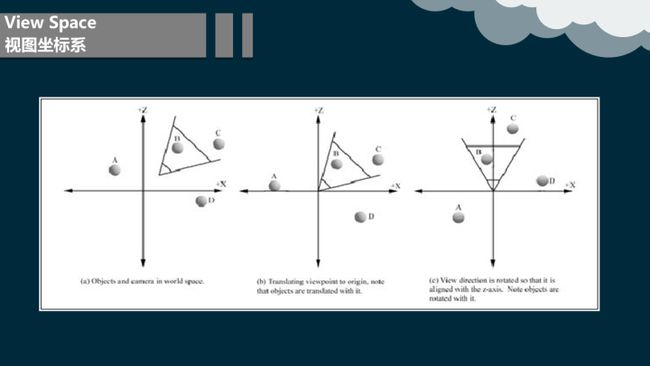
5.3 视图坐标系

 

 

世界坐标系中的几何图与照相机是相对于世界坐标系而定义的，如图2.10所示。然而在世界坐标系中当照相机是任意放置和定向时，投影和其它一些操作会变得困难或低效。为了使事情变得更简单，我们将照相机平移变换到世界坐标系的源点并把它的方向旋转至朝向Z轴的正方向，当然，世界坐标系中的所有物体都将随着照相机的变换而做相同的变换。这个变换就叫做视图坐标系变换（view space transformation）。

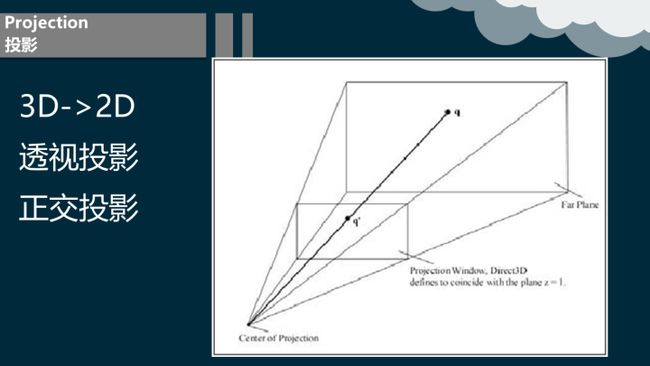
5.4 投影

 

 

视图坐标系的主要任务就是将3D场景转化为2D图像表示。这种从n维转换成n-1维的过程就叫做投影。投影的方法有很多种，但是我们只对一种特殊的投影感兴趣，那就是透视投影。因为透视投影可以使离照相机越远的物体投影到屏幕上后就越小，这可以使我们把3D场景更真实的转化为2D图像。

投影变换的实质就是定义可视体，并将可视体内的几何图形投影到投影窗口上去。

6 色彩和纹理

 

 

一个纹理实际上就是一个位图。从这个意义上来讲，当纹理一词被用于计算机图形学时，它就有了一个明确的定义。从语义学角度来讲，纹理一词既是指一个物体上颜色的模式，又是指物体表面是粗糙的还是光滑的。

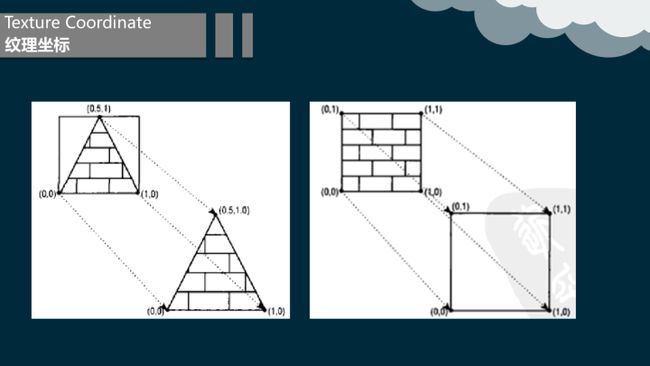
6.1 纹理坐标

 

 

纹理实际上是一个二维数组，它的元素是一些颜色值。单个的颜色值被称为纹理元素（texture elements）或纹理像素（texel）。每一个纹理像素在纹理中都有一个唯一的地址。这个地址可以被认为是一个列（column）和行（row）的值，它们分别由U和V来表示。

纹理坐标位于纹理空间中。也就是说，它们和纹理中的(0,0)位置相对应。当我们将一个纹理应用于一个图元时，它的纹理像素地址必须要映射到对象坐标系中。然后再被平移到屏幕坐标系或像素位置上。

6.2 纹理过滤

渲染一个图元时，会将三维图元映射到二维屏幕上。如果图元有纹理，就必须用纹理来产生图元的二维渲染图象上每个像素的颜色。对于图元在二维屏幕上图象的每个像素来说，都必须从纹理中获得一个颜色值。我们把这一过程称为纹理过滤（texture filtering）

进行纹理过滤时，正在使用的纹理通常也正在被进行放大或缩小。换句话说，这个纹理将被映射到一个比它大或小的图元的图象上。纹理的放大会导致许多像素被映射到同一个纹理像素上。那么结果看起来就会使矮矮胖胖的。纹理的缩小会导致一个像素被映射到许多纹理像素上。其结果将会变得模糊或发生变化。要解决这些问题，我们可以将一些纹理像素颜色融合到一个像素颜色上。

每种类型的纹理过滤都有各自的优缺点。例如，线性过滤会产生锯齿状的边缘和矮胖的效果。但是，它对系统的消耗却是最小的。另一方面，mipmap过滤的效果通常是最好的，特别是和各项异性过滤混合使用时。但是它却需要很大的内存消耗。

6.2.1 双线性过滤

 

 

线性过滤方法是双线性过滤（bilinear filtering）。和最近点采样一样，双线性过滤首先要计算一个纹理像素的地址，这个地址通常不是整数地址。然后，找到一个地址最接近的整数地址纹理像素。另外，渲染模块还要计算与最近采样的点相邻的四个纹理像素的加权平均（weighted average）。

6.2.2 各项异性过滤

 

 

各向异性是对一个三维物体纹理像素的可见的变形，这个物体的表面朝向屏幕平面，并与之有一定的角度。各向异性图元的像素在映射到纹理像素时，它的形状会发生变形。

各向异性纹理过滤可以和线性过滤或mipmap过滤联合使用。

6.2.3 Mipmap

 

 

一个mipmap就是一系列的纹理，每一幅纹理都与前一幅是相同的图样，但是分辨率都要比前一幅有所降低。mipmap中的每一幅或者每一级图象的高和宽都比前一级小二分之一。Mipmap并不一定必须是正方形。

 

　　高分辨率的mipmap图象用于接近观察者的物体。当物体逐渐远离观察者时，使用低分辨率的图象。Mipmap可以提高场景渲染的质量，但是它的内存消耗却很大。

6.3 纹理环绕

 

 

一般来说，分配的U、V纹理坐标值都在0.0到1.0范围内（包括它们）。但是，如果我们分配了超出这个范围的纹理坐标，可能会得到一些特别的纹理效果。

通过设置纹理寻址模式，我们就可以在纹理坐标超出范围时进行控制。

6.3.1 重复

图象在表面上重复出现。忽略纹理坐标的整数部分，并将纹理图的拷贝粘贴在物体表面上,这样才能做到无缝连接。

6.3.2 截取

将大于1.0的数值设置为1.0，将小于0.0的数值设置为0.0，即将超出[0.0,1.0]范围的数值截取到[0.0,1.0]范围内，

这样会导致纹理边缘的重复。

6.3.3 镜像重复

图象在物体表面上不断重复，但是每次重复的时候对图象进行镜像或者反转。这样在纹理边缘处比较连贯。

6.3.4 边界截取

在[0.0,1.0]范围外的参数值用单独定义的边界颜色或纹理边缘进行绘制。适合于绘制物体表面的贴花纸。

 

6.3.5 边缘截取

总是忽略边界。处于纹理边缘或者靠近纹理边缘的纹理单元都用作纹理计算，但是不包括边界上的纹理单元。

 

6.4 立方体纹理

 

 

立方体纹理是一种特殊的纹理技术，它用6幅二维纹理图像构成一个以原点为中心的纹理立方体。对于每个片段，纹理坐标(s, t, r)被当作方向向量看待，每个纹素(texel)都表示从原点所看到的纹理立方体上的图像。

基本上说cubemap它包含6个2D纹理，这每个2D纹理是一个立方体（cube）的一个面，也就是说它是一个有贴图的立方体。你可能会奇怪这样的立方体有什么用？为什么费事地把6个独立纹理结合为一个单独的纹理，只使用6个各自独立的不行吗？这是因为cubemap有自己特有的属性，可以使用方向向量对它们索引和采样。想象一下，我们有一个1×1×1的单位立方体，有个以原点为起点的方向向量在它的中心。

6.5 点精灵

 

 

6.5.1 什么是点精灵

openGL的图形由顶点构成，以后利用顶点进行纹理的映射。点精灵就是，一个顶点被当作一个精灵来处理。特别之处就是，一个顶点也可进行纹理贴出。例如，原来是个顶点构成的一个矩形，现在一个顶点就可以完成了。瞬间我们就可以想想，粒子效果，那些云雾水流火花什么的用了点精灵，就可以瞬间减少3个顶点的计算，glDrawArrays使用GL_POINT就可以了，完全也不需要什么顶点索引了。这是非常诱人的效率。

6.5.2 点精灵的局限

一个顶点缩放都必须是矩形。并且大小的最大最小值是有范围的。既然是一个纹理映射到一个顶点上，那么纹理映射就和原来完全不同，有些复杂。可能会抵消掉一些性能的优势。

6.6 纹理压缩

 

 

贴图是在 3D 场景中，增加真实性的一个重要的工具。就像一般的影像一样，贴图的大小愈大，它的图像就愈精细。事实上，贴图往往需要比一般的影像更大。因为，在 3D 场景中，观察者可能会很靠近贴图，使得贴图需要放大很多倍，而造成模糊的现象。所以，一般来说，如果可能的话，贴图愈大就愈好。

不过，贴图是非常占用内存空间的。

常用的图像文件格式有BMP，TGA，JPG，GIF，PNG等；

不过象JPG这种常见图像压缩格式对于多数应用的内存占用和显示总线带宽占用并没有直接的好处，因为还得解压缩成原始像素再传给显卡，而且还有加载时的解碼计算负担。这是因为显卡的纹理解碼硬件不理解JPG格式。所以，在没有显卡硬件支持的情况下，用压缩格式保存纹理没什么意义，特别是对于手持移动设备来说，解碼象JPG这种复杂格式是很浪费电的。

考虑到现代游戏对纹理图片的严重依赖，及相应的对视频总线的巨大压力，硬件实时解压缩获得了广泛的支持，不过这个还没有一种格式获得多个厂家的支持。纹理数据的格式则没有标准，要参考厂商的SDK或文档获得format值。这也就意味着，使用了压缩纹理之后就不能跨平台了。

纹理格式是能被GPU所识别的像素格式，能被快速寻址并采样。

在Beers，Agrawala和Chaddha于1996发表的一篇影响深远的论文基于已压缩纹理的渲染[1]中，他们列举四项纹理压缩的特点，使其不同于其他图像压缩技术。

解压速度：由于最好能直接从已压缩的纹理直接渲染，为了尽可能地不影响性能，解压缩要尽可能快。

随机访问：由于几乎不可能预测纹素被访问的顺序，任何纹理压缩算法必须允许对其中纹素的随机访问。所以几乎所有的纹理压缩算法都以块为单位压缩和存储纹素，当某一纹素被访问时，只有同一块中若干纹素被读取和解压缩。这项需求也排除了很多压缩率较高的图像压缩方式，例如JPEG和行程长度编码。

压缩率和图像质量：由于人眼的不精确性，相比于其他应用领域，图像渲染更适宜使用有损数据压缩。

编码速度：纹理压缩对压缩速度要求不高，因为绝大多数情况下，纹理只需要进行一次压缩。

由于其数据访问模式是事先知道的，纹理压缩常作为整个绘图管线的一部分，在绘制时对动态地已压缩数据进行解压缩。而反过来绘制管线也可以通过纹理压缩技术来降低对于带宽和存储的需求。在纹理贴图中，已压缩纹理和没有经过压缩的纹理使用起来基本没有区别，都可以被用来存储颜色数据或其他数据，例如凹凸贴图或法线贴图，也都可以和Mipmapping或各向异性过滤等共同使用。

6.6.1 主要GPU厂商及支持的纹理压缩算法

 

 

7 粒子系统

 

 

7.1 效果预览

 

 

粒子系统表示三维计算机图形学中模拟一些特定的模糊现象的技术，而这些现象用其它传统的渲染技术难以实现的真实感的效果。经常使用粒子系统模拟的现象有火、爆炸、烟、水流、火花、落叶、云、雾、雪、尘、流星尾迹或者象发光轨迹这样的抽象视觉效果等等。

 

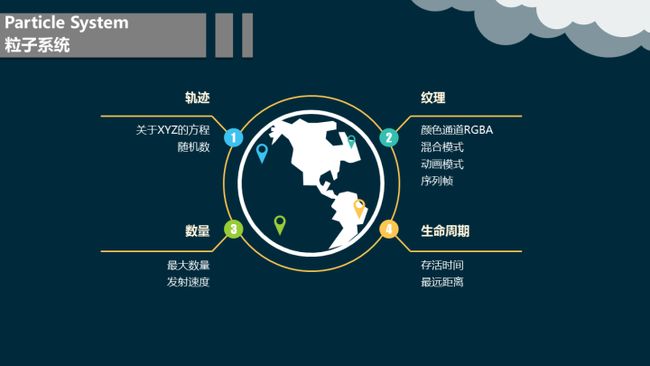
7.2 主要参数

 

 

什么是粒子系统？粒子系统是由总体具有相同的表现规律，个体却随机表现出不同的特征的大量显示元素构成的集合。

这个定义有几个要素：

1、 群体性：粒子系统是由“大量显示元素”构成的。因此，用粒子系统来描述一群蜜蜂是正确的，但描述一只蜜蜂没有意义。

2、 统一性：粒子系统的每个元素具有相同的表现规律。比如组成火堆的每一个火苗，都是红色，发亮，向上跳动，并且会在上升途中逐渐变小以至消失。

3、 随机性：粒子系统的每个元素又随机表现出不同特征。比如蜂群中的每一只蜜蜂，它的飞行路线可能会弯弯曲曲，就象布郎运动一般无规则可寻，但整个蜂群，却是看起来直线向一个方向运动（这就是上一点所说的统一性）。

 

8 数学基础

 

 

这一部分是很简单的，对于不同数学知识背景的读者来说都容易阅读。对于想了解更多更全的这方面信息的读者，请查看有关线性代数和高等数学的书籍。

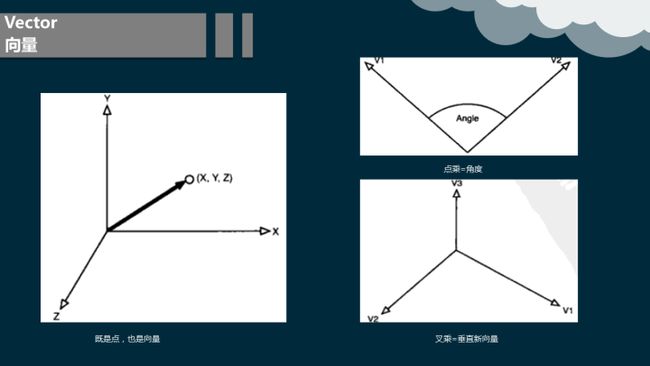
8.1 向量

 

 

几何学中，我们用有向线段表示向量。向量的两个属性是他的长度和他的顶点所指的方向。因此，可以用向量来模拟既有大小又有方向的物理模型。例如，以后我们要实现的粒子系统。我们用向量来模拟粒子的速度和加速度。在3D计算机图形学中我们用向量不仅仅模拟方向。例如我们常常想知道光线的照射方向，以及在3D世界中的摄象机。向量为在3维空间中表示方向的提供了方便。

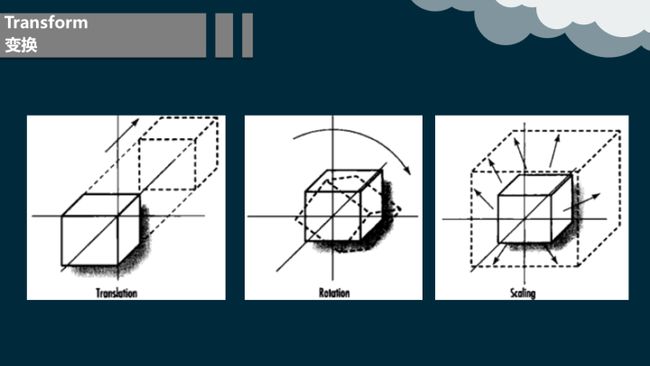
8.2 变换

 

 

3D空间中最常用的变换主要是，平移，旋转，缩放

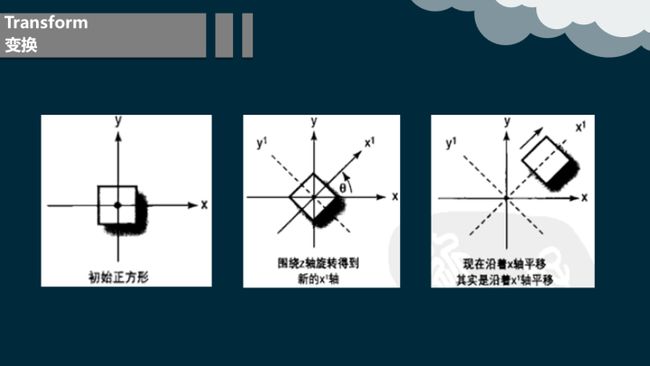
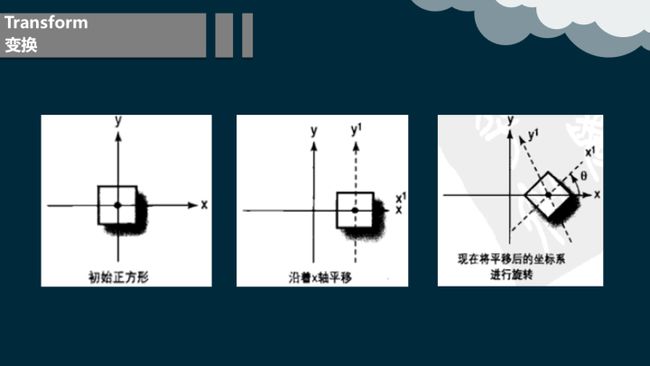
8.2.1 变换的顺序

 

 

变换作用的顺序会影响变换最终的结果。

 

 

通过使用矩阵相乘把3个变换矩阵合成一个矩阵。注意我们必须按实际应用的顺序来进行矩阵相乘。

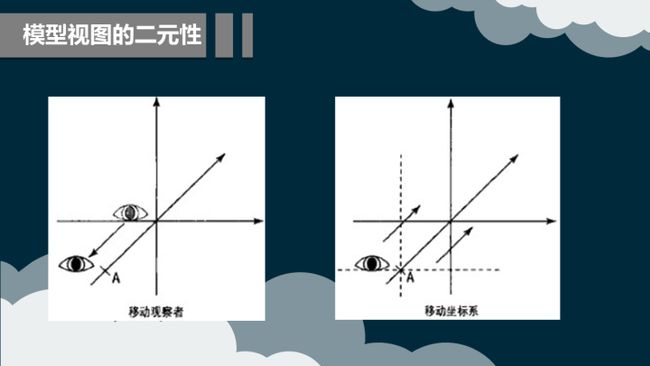
8.2.2 模型视图的二元性

 

 

视图和模型变换对场景外部的最终效果来看是一样的，将两者区分开纯粹是为了程序员方便。将对象向后移动和将参考坐标系向前移动在视觉上没有区别。

 

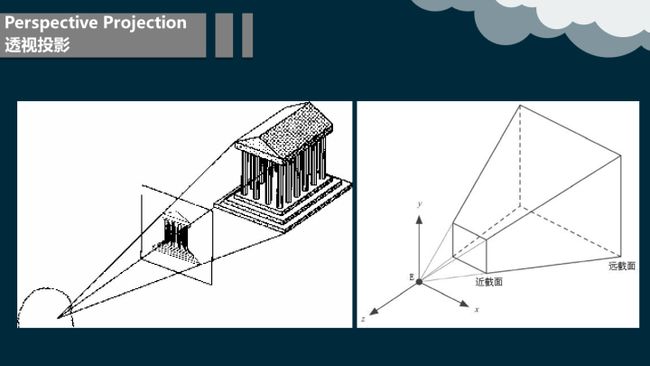
8.2.3 透视投影

 

 

透视投影属于中心投影。透视投影图简称为透视图或透视，它是从某个投射中心将物体投射到单一投影面上所得到的图形。透视图与人们观看物体时所产生的视觉效果非常接近，所以它能更加生动形象地表现建筑外貌及内部装饰。在已有实景实物的情况下，通过拍照或摄像即能得到透视图；对于尚在设计、规划中的建筑物则作图（手工或计算机）的方法才能画出透视图。透视图以渲染、配景，使之成为形象逼真的效果图。

透视投影符合人们心理习惯，即离视点近的物体大，离视点远的物体小，远到极点即为消失，成为灭点。它的视景体类似于一个顶部和底部都被切除掉的棱椎，也就是棱台。这个投影通常用于动画、视觉仿真以及其它许多具有真实性反映的方面。

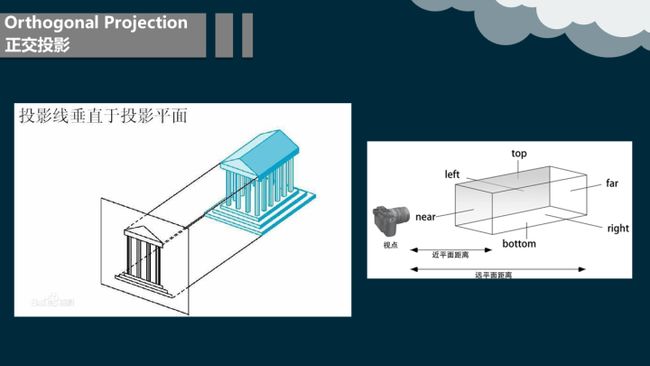
8.2.4 正交投影

 

 

投影线垂直于投影面的投影属于正交投影 ，属于平行投影的一种。