一、关于三次作业的思路
虽然说经过了寒假里两次pre项目的练习,但也只是熟悉了一下java的基本语法和idea的用法,但是对面向对象这样的一种全新的编程模式还是很不熟悉。上过课后虽然有增加了关于面向对象的基础知识,但是在完成作业的时候思路还是不自主的往面向过程的方向去靠拢,这一点希望在今后的学习中有所改进。
第一次作业:简单多项式求导
可以看到第一次作业还是非常面向过程的,我的思路是在PolyComputer这个主类先对输入进来的字符串形式的多项式进行预处理:
- 通过parsePoly方法,将输入进来的字符串进行解析,返回一个List,List中的每一项是用来连接项的正负号(排除了可能出现指数中带符号整数的符号)和项本身,并且考虑到在下一步中对符号的运算会牵扯到List中的添加元素的删除元素,在此使用了删除和添加元素效率较高的数据结构linkedlist;
- 将解析好的linkedlist传入到simplify方法中,对连续出现的符号进行化简,使得每一项之间都由一个单独的符号来连接
接下来就是遍历经过预处理后,储存多项式的linkedlist,根据符号,转换为Poly对象,而Poly中的每一项是一个Item对象,然后求导,合并同类项,输出。
由于第一次作业非常简单,加上对面向对象的不熟悉,就采用了这样一种十分粗暴(我认为刚开始对多项式字符串的处理十分粗暴,并没有按照指导书中的形式化表述来解析多项式)并且粗糙的方式来进行,互测阶段被hack的一个点是由于粗心大意,在Item的toString方法中对系数为1的情况造成了类似“1x**2”这样的format error,也算是在输出阶段没有考虑周全的一个表现吧。
下面是复杂度分析表:
可以看出由于使用了这种粗糙的处理方式,整体复杂度偏高,也是今后需要改进的一个地方。
第二次作业:包含了幂函数的简单三角函数的多项式求导
第二次作业加入了对WRONG FORMAT的判断,所以不得不使用正则表达式来的对输入的多项式进行判断格式。最先想到的方法就是对指导书中的形式化表述进行向正则表达式的翻译,通过一步一步的迭代,最终得到了一个能够匹配整个多项式的正则表达式,故在第一次作业的基础上,只要在对多项式字符串的预处理之前进行一次对输入字符串的匹配过程(PolyComputer中的checkFormat()方法)就可以了,匹配成功则正常进行预处理,否则输出“WRONG FORMAT!”
第二次作业在第一次作业的基本思路上差别不大,只是并没有对按照我们平时的链式法则以及乘法法则进行求导,而是将每一项都格式化为"c*x**n*sin(x)**m*cos(x)**k"的形式,每一项的求导只需要在这个基础上进行系数的指数的相应变换即可。
相对于第一次作业来说改进的地方在与使用了简单工厂模式,在工厂中对每一个因子进行识别,从而返回不同类型的因子,再加入多项式中。
互测中被hack的一个点是由于在组成Poly类的过程中就将三个变量因子的指数进行了合并,导致对于一些原本输入时没有超过10000,但是合并后超过10000的样例错误地输出了WF。
下面是复杂度分析:
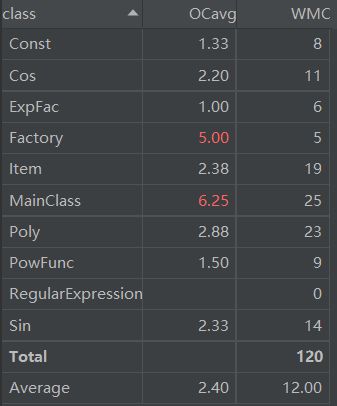
第三次作业:支持嵌套的多项式求导
第三次作业由于在三角函数中支持嵌套,这给在解析表达式以及判断WRONG FORMAT的时候增加了不小的挑战,在翻阅讨论区各位dalao各显神通的解决方法后,我采取了一种将三角函数因子中的内容换成@,表达式因子替换成#的方法,再对原来的正则表达式进行一些小小的改动,即可还使用原来的大正则,对整个表达式进行直接的格式判断。
解析完成后则是通过一个Factor接口来对常数因子Const、表达式因子ExpFac、幂函数因子PowFunc、三角函数因子Sin和Cos进行归一化的处理,由这五个因子来分别实现Factor接口。
下面是复杂度分析:
二、心得体会
总体来说的话对这一单元作业的完成情况是不满意的,主要是每次都在周五才开始进行,这样严重导致了时间的不足,无法在如此短的时间内进行充分的思考和设计,就更没有时间来进行在本地的自动化测试,就开始从匆匆上手,除了第一次作业的由于非常简单,其他的两次作业的结构都非常的混乱。并且在第一次作业中甚至是第二次作业中都没有考虑后面作业可能会出现的状况,留下一些扩展性的空间,因此在每一周的的作业进行之前都要进行一定程度上的重构,导致了这三次作业之间的迭代程度并不是很高。