Matlab计算协方差矩阵时,维度用列表示还是用行表示

均值、方差和标准差计算公式

均值：
$$\overline{X}=\frac{{\sum }_{i=1}^n(x_i-\overline{x})}{n}$$

方差：
$$s^2=\frac{{\sum }_{i=1}^n(x_i-\overline{x}{)}^2}{n}$$

标准差：
$$s=\sqrt{\frac{{\sum }_{i=1}^n(x_i-\overline{x}{)}^2}{n}}$$

方差是衡量随机变量或一组数据时离散程度的度量。方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。（摘自百度百科）

补充：有方差来描述变量与均值的偏离程度，那又搞出来个标准差干什么呢？
方差与要处理的数据的量纲是不一致的，虽然能很好的描述数据与均值的偏离程度，但是处理结果是不符合我们的直观思维的。
举个例子：一个班级里有60个学生，平均成绩是70分，标准差是9，方差是81，成绩服从正态分布，那么我们通过方差不能直观的确定班级学生与均值到底偏离了多少分，通过标准差我们就很直观的得到学生成绩分布在[61,79]范围的概率为0.6826，即约等于下图中的34.2%*2

总的来说，均方差是数据序列与均值的关系，而均方误差是数据序列与真实值之间的关系。
参考

---

协方差矩阵

标准差和方差一般是用来描述一维数据的，但现实生活我们常常遇到含有多维数据的数据集。比如统计多个学科的考试成绩。面对这样的数据集，我们当然可以按照每一维独立的计算其方差，但是通常我们还想了解这几科成绩之间的关系，这时，我们就要用协方差，协方差就是一种用来度量两个随机变量关系的统计量，其定义为：
$$cov(X,Y)=\frac{{\sum }_{i=1}^n(X_i-\overline{x})(Y_i-\overline{Y})}{n-1}$$

【协方差是衡量两个变量同时变化的变化程度。协方差大于0表示 $x$ 和 $y$ 若一个增，另一个也增；小于0表示一个增，一个减。如果 $x$ 和 $y$ 是统计独立的，那么二者之间的协方差就是０。但是协方差是０，并不能说明 $x$ 和 $y$ 是独立的。协方差绝对值越大，两者对彼此的影响越大，反之越小。协方差是没有单位的量。】

从协方差的定义上，也可以看出一些显而易见的性质，如：
$(1)cov(X,X)=var(X)—表示X的方差$
$(2)cov(X,Y)=cov(Y,X)$

需要注意的是，协方差也只能处理二维问题，那维数多了自然就需要计算多个协方差。从而引入协方差矩阵，其定义为：
$$C_{n\ast n}=（c_{i,j},c_{i,j}=cov(Di{m}_i,Di{m}_j)）$$

举例：假设数据集 $x,y,z$三个维度，则协方差矩阵为：

可见，协方差矩阵是一个对称的矩阵，而且对角线是各个维度上的方差。

个人遇到的困惑：在使用Maltab的cov、eig和pca等各函数时，传入的参数究竟是列表示维度还是行表示维度

首先必须明确的一点是：协方差矩阵计算的是不同维度之间的协方差，而不是不同样本之间的。
其次：样本矩阵的每行是一个样本，每列为一个维度。

---

上代码说明：
(1)用Matlab自带的数据

load('hald','ingredients')
ingredients = ingredients';

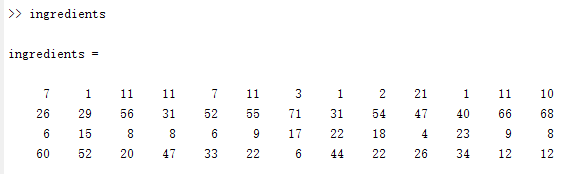
此时，ingredients表示4个样本，每个样本的所包含的维度是13维。（即13列）

(2)去均值
在方差、标准差和协方差的计算公式中都可发现，每一维的数据 $x_i$ 需要减去该维度的均值 $\overline{x}$。
因此，首先将每一维数据的减去均值以后，代入方差、标准差和协方差计算公式时，只需要对每个数据直接求平方和即可。

meanValue = mean(ingredients);   % 计算每一维度的均值
meanValueMatrix = repmat(meanValue,size(ingredients,1),1);
ingredients = ingredients - meanValueMatrix; % 每个数据减去对应维度的均值

(3)计算协方差矩阵
【这儿我并没有根据协方差的公式去计算，即第一列维度与其它各列维度的相乘求和以后在除以样本数。采用了另外一个计算方式：$\frac{1}{n-1}{X}^{T}X$】

这儿还有一个小坑：
假设 $X$ 为 $m\ast n$ 的矩阵，
有的文章对协方差的计算写为： $协方差矩阵=\frac{1}{n-1}X{X}^T$
而有的文章写为：$协方差矩阵=\frac{1}{n-1}{X}^{T}X$

其实上述两者都没有错。只是在第一种计算里面，$X$ 的每一列是一个样本，而行数表示的是维度（n=样本个数，m=维度）
在第二种计算里面，$X$ 的每一行是一个样本，而列数表示的是维度（m=样本个数，n=维度）

协方差计算：

% 协方差矩阵.其中n=size(ingredients,1),n是样本个数
covMatrix = ingredients' * ingredients / (size(ingredients,1) - 1); 

(4)使用cov函数验证
需要注意的是：matlab计算协方差的函数cov，是按列表示维度，减去每列均值然后计算协方差矩阵的。

load('hald','ingredients')
ingredients = ingredients';
test = cov(ingredients)

---

Matlab的pca函数

仍然使用上面的例子。求出协方差矩阵以后，即可得到协方差矩阵的特征值和特征向量。当特征值按照从大到小排列，取前面k个特征值所对应的特征向量所形成的矩阵，即可对原数据降维。(pca)

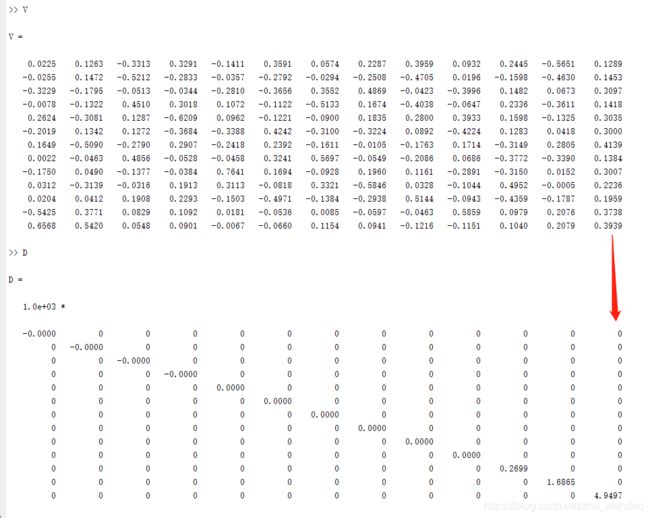
(1)求协方差矩阵的特征值和特征向量

% D是对角矩阵，其对角上的值是特征值。V的每一列对应D上的每一个特征值。如下图箭头
[V,D] = eig(covMatrix);

(2)pca函数对原数据降维

load('hald','ingredients')
ingredients = ingredients';
% coeff是特征向量组成的矩阵,score是降维后的新数据,latent是特征值
[coeff,score,latent] = pca(ingredients);  

特征值和特征向量：

latent与D相比发现，latent是特征值按照从大到小排序，而在D中，特征值是按照从小到大排序。
特征向量一样。