022 囚徒困境中的均衡-----从一篇经典论文说起

1.囚徒困境

　　囚徒困境（Prisoner’s Dilemma）是博弈论的非零和博弈中具代表性的例子，反映个人最佳选择并非团体最佳选择。或者说在一个群体中，个人做出理性选择却往往导致集体的非理性。虽然困境本身只属模型性质，但现实中的价格竞争、环境保护等方面，也会频繁出现类似情况。
　　1950年，由就职于兰德公司的梅里尔·弗勒德（Merrill Flood）和梅尔文·德雷希尔（Melvin Dresher）拟定出相关困境的理论，后来由顾问艾伯特·塔克（Albert Tucker）以囚徒方式阐述，并命名为“囚徒困境”。
　　囚徒困境是博弈论中最经典的一个问题。

2.计算机仿真

　　1992年Martin A. Nowak 和 Rebort M. May在Nature上发表了一篇论文Evolutionary games and spatial chaos,论文采用了一种极为简单的规则就囚徒困境做了仿真。具体内容大家可以查阅这篇文献。下面是核心代码（MATLAB实现）：
　　

% 获取个编辑框以及按钮的数值
var = get(handles.popupmenu2, 'Value');
T = get(handles.edit1, 'String');
R = get(handles.edit2, 'String');
P = get(handles.edit3, 'String');
S = get(handles.edit4, 'String');
L = get(handles.edit5, 'String');
TimeStep = get(handles.edit6, 'String');
T = str2double(T);
R = str2double(R);
P = str2double(P);
S = str2double(S);
L = str2num(L);
TimeStep = str2num(TimeStep);

% 获取初始时刻的模式：随机还是几何对称
if get(handles.Regular, 'Value');
    flag = 1;
elseif get(handles.Random, 'Value')
    flag = 0;
end

%获取初始格局
%CurrrentPayers是当前格局
CurrentPlayers = InitMatrix(flag, L, var);

%TempPlayers是博弈时临时存储当前格局的矩阵
TempPlayers = CurrentPlayers;

%存储策略改变信息的矩阵
Changes = zeros(L);

% Payoff记录当前格局中每个点博弈所获得的总收益（与8个邻居及自己）
%每个个体的收益初始化为0

Payoff = zeros(L);
for t = 1:TimeStep
    Frequency = sum(sum(CurrentPlayers))/(L*L);
    Frequency = roundn(Frequency, -3);
    set(handles.Output, 'String', Frequency);
    axes(handles.axes2);
    axis([0, TimeStep, 0, 1]);
    plot(t, Frequency, '.');
    hold on
    % 同时博弈
    %原论文使用非周期边界

    % 没开始一轮新的博弈，上一局的利益是要清零的。
    % 经常忘记！！！！！！！
    Payoff = zeros(L);
    for i = 1:L
        for j = 1:L
           for m = -1:1
              for n = -1:1%注意T\R\P\S对应的情况
                  % 自己不与自己博弈
                  I = i + m;
                  J = j + n;
                  %无周期边界的编程实现！！！如何最简洁描述
                  if I>0 && I<=L && J>0 && J<=L                                        
                      if CurrentPlayers(i, j)==1 && CurrentPlayers(I, J)==1
                          Payoff(i, j) = Payoff(i, j) + R;
                      elseif CurrentPlayers(i, j)==1 && CurrentPlayers(I, J)==0
                          Payoff(i, j) = Payoff(i, j) + S;
                      elseif CurrentPlayers(i, j)==0 && CurrentPlayers(I, J)==1
                          Payoff(i, j) = Payoff(i, j) + T;
                      elseif CurrentPlayers(i, j)==0 && CurrentPlayers(I, J)==0
                          Payoff(i, j) = Payoff(i, j) + P;
                      end
                  end
              end
           end
        end
    end
    %这么多循环，我想自尽！！！
    for i = 1:L
        for j = 1:L
            TempPayoff = Payoff(i, j);
           for m = -1:1
              for n = -1:1
                  % 自己没必要跟自己再做选择，想清楚！！
                  if m~=0 || n~=0
                      I = i + m;
                      J = j + n;

                      %无周期边界的编程实现！！！如何最简洁描述


                      % 以下代码有一个问题
                      % 实际博弈中人不是一个一个看的
                      % 这里就有一个矛盾了
                      % 语言不便于描述
                      % 这里提出一个 我自己 假设的 理性假设：
                      % 假设最大利益相同时，人更倾向于选择合作。
                      % 当然了，也可以尝试更倾向于背叛，因为背叛可以保证自己不被背叛

                     if I>0 && I<=L && J>0 && J<=L
                          if Payoff(I, J) > TempPayoff
                              TempPlayers(i, j) = CurrentPlayers(I, J);
                              % 这一句也非常容易遗漏
                              %并且注意，不能直接对该位置的收益赋值，因为其还要用来被比较
                              TempPayoff = Payoff(I, J);
                              % 这里最大利益相同时，是选择最大的背叛还是最大的合作？？
                          elseif Payoff(I, J) == TempPayoff && CurrentPlayers(I, J)==0
                              TempPlayers(i, j) = CurrentPlayers(I, J);
                          end
                      end
                  end
              end
           end
        end
    end

    %画策略改变图
    for i = 1:L
        for j = 1:L
            if CurrentPlayers(i, j) == 1 && TempPlayers(i, j) == 1
                Changes(i, j) = 1;
            elseif CurrentPlayers(i, j) == 1 && TempPlayers(i, j) == 0
                Changes(i, j) = 2;
            elseif CurrentPlayers(i, j) == 0 && TempPlayers(i, j) == 1
                Changes(i, j) = 3;
            elseif CurrentPlayers(i, j) == 0 && TempPlayers(i, j) == 0
                Changes(i, j) = 4;
            end
        end
    end
    %指定颜色
    Map = [0 0 1;1 1 0;0 1 0;1 0 0];
    axes(handles.axes1);
    colormap(Map);
    imagesc(Changes);
    drawnow 
    %同步
    CurrentPlayers = TempPlayers;
    % 如需控制速度
    % 这个功能也可以加到GUI上，考虑到空间不够用，
    % 速度也没有特殊要求，可直接在源代码中设定
    pause(0);
end

　　源文件是个GUI,完整文件我可在我的资源或GitHub上找到。

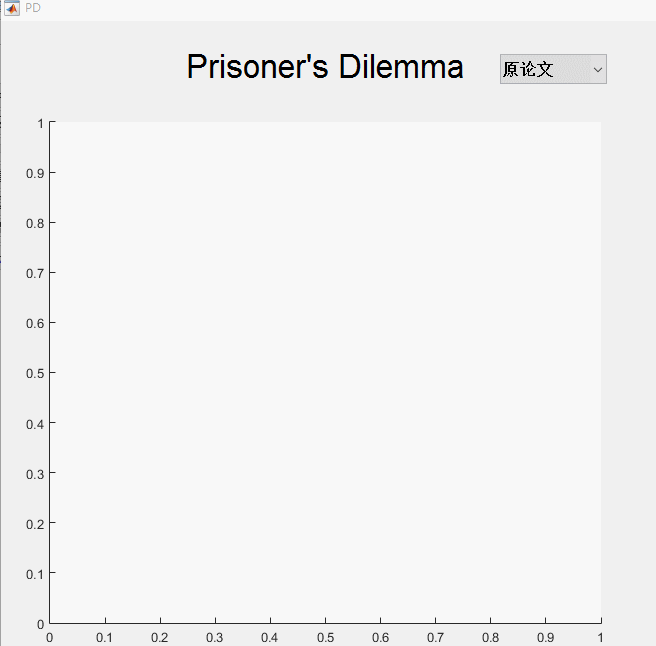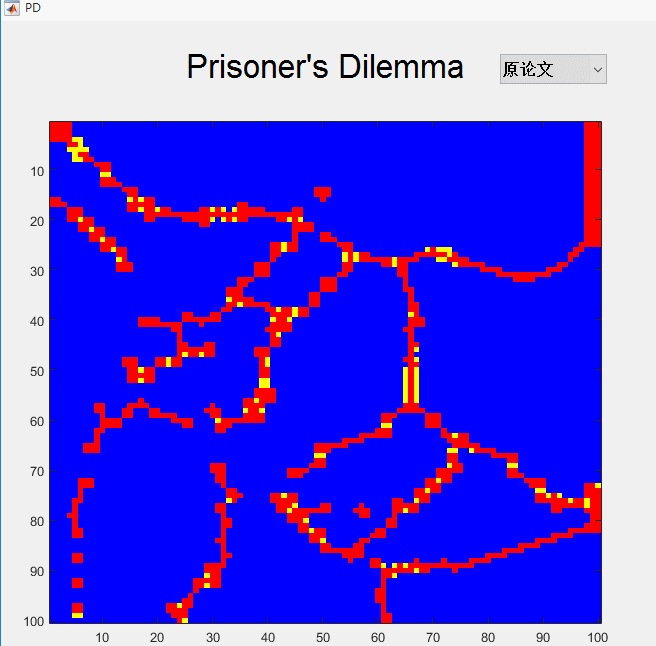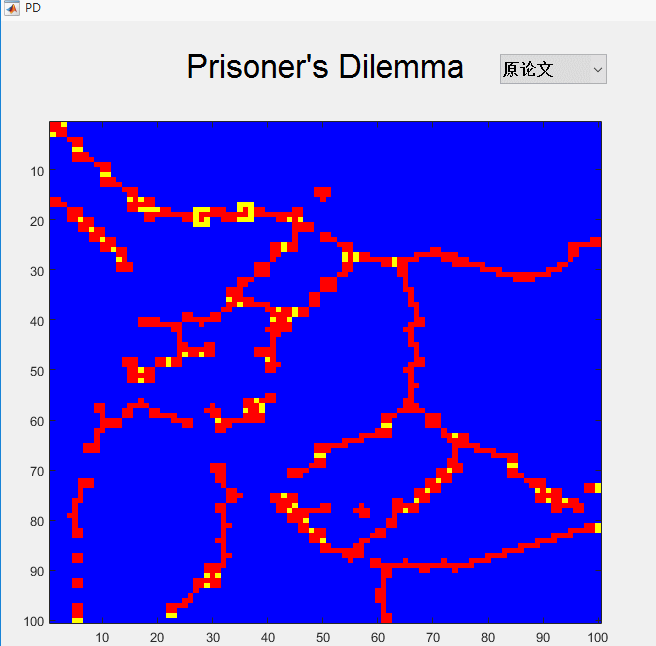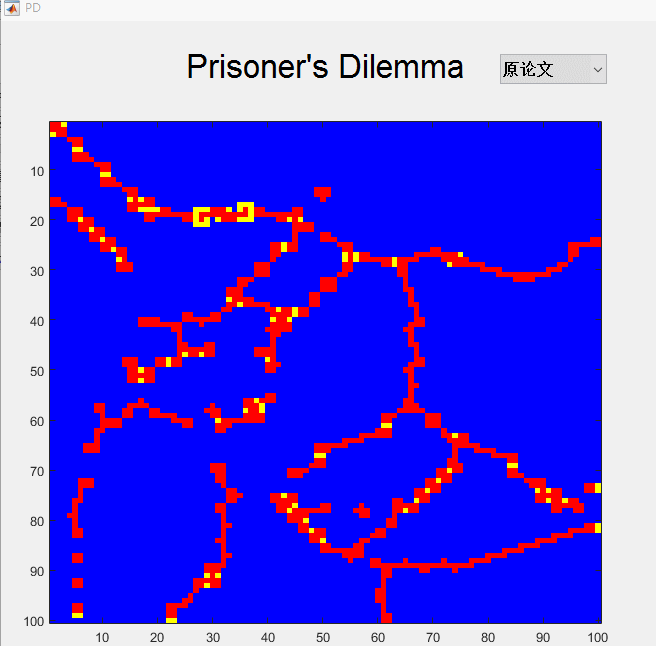
• 稍微放几张仿真图纪念一下，当然了，没看Nowak那篇论文还是看不懂得。。。。。

　　

　　

总结

　　最重要的还是总结，其实这种仿真程序逻辑上并不是太难，主要还是要理清关系，对论文描述的模型有一个深刻的理解，编程是才能不费吹灰之力。以下十几个我遇到的bug：

    % 没开始一轮新的博弈，上一局的利益是要清零的。
    % 经常忘记！！！！！！！
    Payoff = zeros(L);

TempPlayers(i, j) = CurrentPlayers(I, J);
% 这一句也非常容易遗漏
%并且注意，不能直接对该位置的收益赋值，因为其还要用来被比较
TempPayoff = Payoff(I, J);

% 这里最大利益相同时，是选择最大的背叛还是最大的合作
% 这个问题不注意就会导致图形不对称！
% 应先全部比较，然后从中选择，所有的顺序比较都是不对的！