2018-2019赛季多校联合新生训练赛第三场 18-12-08

Problem B：

题目描述
麻雀帕西和青蛙弗洛格是好玩伴，它们经常一起比赛唱歌。但冬天来了，青蛙弗洛格冬眠了，它的睡眠深度是D。麻雀帕西觉得好无聊，于是它想办法要唤醒弗洛格。麻雀帕西只会唱N首歌，第i首歌的音量是Si。每听完一首歌，青蛙弗洛格的睡眠深度就会减少，减少的值等于它听到的歌的音量。当青蛙弗洛格的睡眠深度大于0的时候，它会继续冬眠，当睡眠深度小于或者等于0时，它就会被唤醒了。麻雀帕西会从第1首歌开始唱，唱完第1首歌后如果弗洛格还没醒就接着唱第2首歌，如果唱完第2首歌弗洛格还没醒就接着唱第3首歌，依次类推，如果唱完第N首歌后弗洛格还没醒，那么麻雀帕西又重新从第1首歌开始唱，就像循环播放音乐一样，一直到青蛙弗洛格被唤醒为止，那么麻雀帕西总共唱了多少首歌？

输入
第一行，两个整数： D 和 N。
第二行，N个整数，空格分开，第i个整数就是第i首歌的音量Si。

输出
一个整数，麻雀帕西总共唱了多少首歌后，弗洛格会被唤醒？

样例输入

13  3
5  2  4

样例输出

4

提示

麻雀帕西唱完第2首歌后，青蛙弗洛格睡眠深度变成6，
麻雀帕西唱完第3首歌后，青蛙弗洛格睡眠深度变成2，
麻雀帕西再次唱完第1首歌后，青蛙弗洛格睡眠深度变成-3，青蛙弗洛格会被唤醒。

对80%的数据，1 ≤ D ≤ 10000，1 ≤ N ≤ 50，1 ≤ Si ≤ 100。
另外20%的数据，1 ≤ D ≤ 2000000000，1 ≤ N ≤ 50，1 ≤ Si ≤ 3。

分析：这个题看起来比较简单，似乎暴力模拟就可以出答案，一次一次减，唱完一遍再从第一首开始唱，一直唱到睡眠深度为零或小于零时。
但很不幸，这个题会超时，从那20%的数据就可以看出，题目的目的并不只是想让你完全暴力，所以必须优化。
我们发现，再这几首歌完全唱完以后，如果睡眠深度足够大的话，他可能要继续唱很多遍，所以我的优化方法是：把睡眠深度对所有歌唱一遍的时间取模，然后再加上最后要唱的歌进行模拟。这样会快速很多。

#include
using namespace std;
int main()
{
    long long d,n;
    cin>>d>>n;
    long long a[60];
     int i=0;
    long long t=0;
    long long sum=0;
    for(i=0;i<n;i++)
    {
        cin>>a[i];
        sum+=a[i];
    }
    if(d>sum)
        t=d/sum;
    d%=sum;
    t*=n;
    i=0;
    while(d>0)
    {
        d-=a[i];
        t++;
        i++;
        if(i==n)
            i=0;
    }
    cout<<t;
    return 0;
}

Problem C:进制转化

题目描述
乐乐正在学进制转换，但他老是搞不清楚到底自己是否做对，请你编一程序实现两种不同进制之间的数据转换，帮他检验。

输入
共有三行，第一行是一个正整数，表示需要转换的数的进制n(2≤n≤16)，第二行是一个n进制数，若n>10则用大写字母A～F表示数码10～15，并且该n进制数对应的十进制的值不超过1000000000，第三行也是一个正整数，表示转换之后的数的进制m(2≤m≤16)。

输出
仅一行，包含一个正整数，表示转换之后的m进制数。

样例输入
16
FF
2
样例输出
11111111

分析：这个题是比较基础的进制转化，比较良心的是对应的十进制数都不超过long long ，先转化为10进制，然后再用整除取余的方法，存入栈，然后再把栈中的元素转出来，超过10的用字母输出。

#include
using namespace std;
int main()
{
    int n,m;
    cin>>n;
    string a;
    cin>>a;
    cin>>m;
    int shu[1000];
    int lena=a.size();
    for(int i=0;i<lena;i++)
    {
        if(a[i]<='9')
            shu[i]=a[i]-'0';
        else if(a[i]>='A')
            shu[i]=a[i]-'A'+10;
    }//先把输入数中的每一位，存入数组。
    long long sum=0;
    for(int i=lena-1;i>=0;i--)
    {
        sum+=shu[lena-i-1]*pow(n,i);//转化为10进制，，庆幸不超过long long，超了就不会了。
    }//sum正确
    stack<int> zh;
    while(sum!=0)
    {
        zh.push(sum%m);//入栈
        sum/=m;
    }
    while(!zh.empty())
    {
        if(zh.top()>=10)
            cout<<char('A'-10+zh.top());
        else if(zh.top()<=9)
            cout<<char(zh.top()+'0');
        zh.pop();
    }
    return 0;
}

Problem E :取数排列

题目描述
取1到N共N个连续的数字（1≤N≤9），组成每位数不重复的所有可能的N位数，按从小到大的顺序进行编号。当输入一个编号M时，就能打印出与该编号对应的那个N位数。例如，当N＝3时，可组成的所有三位数为：

那么，输入编号M＝2时，则输出132。

输入
包括两个数，即正整数N（1 <= N <= 9）和正整数M（1 <= M <= 362880）。

输出
只有一行，即与输入的编号M对应的那个N位数。

样例输入

3 2

样例输出

132

分析：这个题就是将数字进行全排列，利用dfs，只需要每次出一个数后m减一，一直到0就可以了。

#include
using namespace std;
int a[10],book[10],n;
int m;
void dfs(int step)
{
	int i;
	if(step==n+1)
	{
	    m--;
	    if(m==0)
		for(i=1;i<=n;i++)
		{
			cout<<a[i];
		}
		return;
	}
	for(i=1;i<=n;i++)
	{
		if(book[i]==0)
		{
			a[step]=i;
			book[i]=1;
			dfs(step+1);
			book[i]=0;
		}
	}
	return;
}
int main()
{
	cin>>n>>m;
	dfs(1);
	return 0;
}

Problem E：懒洋洋找朋友

题目描述
最近电视上热播“喜羊羊与灰太狼”，大家都说“做人要做懒羊羊”，为什么呢？因为他不愿意多做一个动作、不愿意多动一个脑筋，甚至懒得张嘴吃饭，简直是懒的无与伦比！

话说羊村的羊还真多啊！每周一早晨，羊村老村长慢羊羊同志学着人类的学校，把所有羊列队在广场上进行思想教育，主要是保持警惕防止狼类的攻击，当然也包括对懒羊羊之类的“异类”进行批评教育。

羊群列队成一个 m*n 的方阵，每只羊站在一个格子里，而且是长期固定的，便于点名啊：）晕倒！当然，这样一来的好处是，大家都知道自己的朋友站在哪个位置，虽然它们可能互相看不见，但心里都知道，并且在老村长进行无聊的训教时，大家都还想赶快结束赶快找离自己最近的朋友交流周末的开心事呢？

懒羊羊也想尽快找到自己的好朋友聊天，但是他既不愿意多走路、又不愿意动脑筋去想怎么走，所以就请智羊羊同学帮它编个程序，以便快速定位找到离它最近的一位好朋友。

如果你是智羊羊，你怎么完成这个任务呢？

输入
第 1 行为两个整数 m 和 n，2<=m,n<=100。
第 2 行为懒羊羊的位置 x,y，表示在第 x 行 y 列。
以 下 m 行 为一 个 m*n 的数字 方阵，所 有 a[i,j]的 值相等的表示是好 朋友，1<=a[i,j]<=100。
每行的两个数之间都有一个空格分隔。

输出
输出一行两个数 x1,y1，表示懒羊羊最近的一个朋友的位置在第 x1 行 y1 列，之间用一个空格隔开。
如果最近的的朋友不只一个，则输出 x1 最小的，如果还不唯一则输出 y1 最小的。
数据保证懒羊羊一定有朋友。

样例输入
4 4
1 2
2 1 2 1
1 3 1 3
2 1 2 2
2 2 1 3
样例输出
1 4

提示
懒羊羊（1，2）有 5 个朋友，其中 3 个朋友（2，1）、（2，3）、（1，4）离它的距离都是一样的（2），但是其中的 x1=1 是最小的。
分析：这个题再读题的时候出现了偏差，对那个距离理解错了，，我一开始以为周围一圈距离都是最近的，实际上d=|x-i|+|y-k|这是距离。距离不会表示，而且最后的排序规则也不会写，再次参考了马鸿儒同学的题解。https://www.cnblogs.com/baccano-acmer/p/10089592.html

#include
using namespace std;
struct node
{
    int x,y,d;
}ans[100];
bool com(node a,node b)
{
    return a.d==b.d?a.x==b.x?a.y<b.y:a.x<b.x:a.d<b.d;//排序规则，优先级从左到右，满足条件时往左一个判断。
}
int Map[110][110];

int main()
{
    int m,n;
    cin>>m>>n;
    int x,y;
    cin>>x>>y;
    for(int i=1;i<=n;i++)
        for(int k=1;k<=m;k++)
    {
        cin>>Map[i][k];
    }
    int t=0;
    for(int i=1;i<=n;i++)
        for(int k=1;k<=m;k++)
        {
            if(Map[x][y]==Map[i][k]&&!(x==i&&y==k))
            {
                ans[t].x=i;
                ans[t].y=k;//存坐标
                ans[t].d=abs(x-i)+abs(y-k);//计算距离
                t++;
            }
        }
    sort(ans,ans+t-1,com);//排序规则
    cout<<ans[0].x<<' '<<ans[0].y;
}

Problem G:求满足条件的数

题目描述
输入N(n<=32767)，输出N以内的整数(包括N)，使其数字之和为15，每行输出8个数。输出场宽为6。

输入
只包括一个整数N。

输出
符合条件的数。

样例输入

200

样例输出

   69    78    87    96   159   168   177   186
  195

分析：对每一个数取各个位数相加为15即满足条件，重点为场宽为6，需要用printf("%6d",a)输出。

#include
using namespace std;
int main()
{
    int n;
    cin>>n;
    int k=0;
    int a;
    for(int i=0;i<=n;i++)
    {
        a=i;
        int sum=0;
        while(a!=0)
        {
            sum+=a%10;
            a/=10;
        }
        if(sum==15)
        {
            printf("%6d",i);//场宽6
            k++;
        }
        if(k==8)//8个数换行
        {
            cout<<endl;
            k=0;
        }
    }
    return 0;
}

Problem K：移动次数最少

题目描述

有n堆糖果（2≤n≤200），排成一行，编号分别为1,2,…n。
已知每堆糖果有一定的颗数，且颗数之和均为n的倍数。移动各堆中的任意颗糖果，使每堆的数量达到相同，且移动次数最少。
移动规则：
每次可以移动任意的糖果颗数，第1堆可以移向第2堆，第2堆可以移向第1堆或第3堆,。。。。。。 第n 堆只可以移向第n -1堆。
例如，当n=4时：
堆号 1 2 3 4
颗数 9 8 17 6
移动的方法有许多种， 其中的一种方案：
① 第3堆向第4堆移动4颗，成为：9 8 13 10
② 第3堆向第2堆移动3颗，成为：9 11 10 10
③ 第2堆向第1堆移动1颗，成为：10 10 10 10
经过三次移动，每堆都成为10颗。

输入

有两行。
第一行一个整数n。
第二行n个整数，用空格分隔。

输出

一个整数（表示最少移动次数）。

样例输入
9　8　17　6

样例输出
3

这个题实在是想不到怎么贪心，后来参考lyj的题解，从第一堆开始，不够的用右边的填，一直达到平均数，多的往右挪，一直到平均数。至于为啥这个就是最少的情况：我的理解是没有出现重复或者说来回搬动的情况，需要移动的每一份糖果都没有走重复的路线，所以最后移动次数最少。

#include
using namespace std;
int main()
{
    int n;
    cin>>n;
    int a[210];
    int sum=0;
    for(int i=0;i<n;i++)
    {
        cin>>a[i];
        sum+=a[i];
    }
    int pj;
    pj=sum/n;
    int t=0;
    for(int i=0;i<n-1;i++)
    {
        if(a[i]==pj)
            continue;
        if(a[i]!=pj)
        {
            a[i+1]+=a[i]-pj;
            t++;
        }
    }
    cout<<t;
    return 0;
}

Problem N:小球

题目描述
有R个红色盒子和B个蓝色盒子，还有R个红色小球和B个蓝色小球。每个盒子只能装一个小球，每个小球都要放在一个盒子里。如果把一个红色小球放在一个红色盒子里，那么得分是C。如果把一个蓝色小球放在一个蓝色盒子里，那么得分是D。如果把一个红色小球放在一个蓝色盒子里，那么得分是E。如果把一个蓝色小球放在一个红色盒子里，那么得分也是E。现在给出R，B，C，D，E。应该如何放置这些小球进盒子，才能使得总得分最大？输出最大的总得分。

输入
一行，5个整数，分别是R，B，C，D，E。（1 ≤ R ≤ 100，1 ≤ B ≤ 100， -1000 ≤ C，D，E ≤ 1000）

输出
一个整数，最大总得分。

样例输入
2  3  100  400  200
样例输出
1400

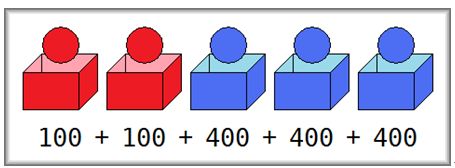
分析：因为相同颜色的球与盒的数目相同，所以只要有蓝球放入红盒，那么就一定有相同数量的红球入蓝盒，所以只有两种情况：1.完全颜色相同，2.数量少的全部放入不同色的盒子，然后这两种情况进行比较，输出最小的即可。

#include
using namespace std;
int main()
{
    int R,B,C,D,E;
    cin>>R>>B>>C>>D>>E;//红放对c，蓝放对d，放错e
    int a,b;
    if(R>B)
        a=B*2*E+(R-B)*C;
    else
        a=R*2*E+(B-R)*D;
    b=R*C+B*D;
    cout<<max(a,b);
    return 0;
}