「洛谷5017」「NOIP2018」摆渡车【DP，经典好题】

前言

在考场被这个题搞自闭了，那个时候自己是真的太菜了。qwq
现在水平稍微高了一点，就过来切一下这一道$DP$经典好题。
附加一个题目链接：【洛谷】

正文

虽然题目非常的简短，但是解法有很多。
我按照时间复杂度来写一下一些做法。
博主只考虑了一些基于时间的做法，其他的再补。。

时间复杂度：$O(t^{2}n)$

借鉴sooke大佬的想法，把问题抽象成一个数轴。
每一个人上车的时间就是在数轴上可能重合的一个点，一辆公交车抽象成在数轴上的一条长度为m的线段进行一次覆盖。
因为考虑到上下车时间忽略不计，那么就把这个线段看成一个左开右闭的线段。
那么问题就变成了，所有人到覆盖这个点的线段右端点的距离之和，我们的任务就是让这个和最小。
如果文字看不懂，那么就看下图：

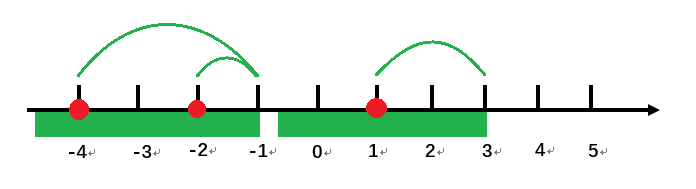
上图中的绿色方块部分就是线段覆盖的区间。
因为我们将公交车抽象成了一个左开右闭的线段，下一辆车最早可以出发的时间。
至于为什么要左开右闭，是因为可以正向的做$DP$。
转化出来了一个非常经典的模型。
$f_i$表示最后一段的右端点是$i$，对于每一个$i$我们需要找到转移到$f_i$的决策。
枚举$j$也就是前一段。
可以得到一个基础的$DP$方程：$f_i=min(f_j+{\sum }_{j<tk\le i}^{}i-t_k)$
其中的$t_k$是每一个人到的时间。也就是数轴上的各个点。
什么优化都没有的$DP$，枚举$i,j,k$。
期望得分：30分

时间复杂度：$O(t^2)$

考虑优化上述$DP$。
先把式子搬下来
$$f_i=min(f_j+\sum _{j<tk\le i}i-t_k)$$
由$\sum$可以发现可以用前缀和优化。
那么我们就试着把这个$\sum$拆成前缀和的形式。
$$\sum _{j<tk\le i}i-t_k=\sum _{j<tk\le i}i-\sum _{j<tk\le i}{t}_k=(psu{m}_i-psu{m}_j)\times i-(tsu{m}_i-tsu{m}_j)$$
其中的$psum$表示的是在区间内符合的个数，$tsum$表示的是在区间内符合的时间的总和。

#include 
using namespace std;
namespace IOstream {
    #define gc getchar
    template <typename T>
    inline void read(T &x) {
        x = 0; T fl = 1; char c = 0;
        for (; c < '0' || c > '9'; c = gc()) if (c == '-') fl = -1;
        for (; c >= '0' && c <= '9'; c = gc()) x = (x << 1) + (x << 3) + (c ^ 48);
        x *= fl;
    }
    #undef gc
} using namespace IOstream;
const int N = 4e6 + 506;
const int inf = 0x3f3f3f3f;
int psum[N], tsum[N], f[N];
int n, m, t;
int main() {
    read(n); read(m);
    if (m == 1) { puts("0"); return 0; }
    for (int i = 1, x; i <= n; i ++) {
        read(x); t = max(x, t);
        psum[x] ++; tsum[x] += x;
    }
    for (int i = 0; i < t + m; i ++) {
        tsum[i] += tsum[i - 1]; 
        psum[i] += psum[i - 1];
    }
    memset(f, inf, sizeof(f));
    for (int i = 0; i < t + m; i ++) {
        f[i] = psum[i] * i - tsum[i];
        for (int j = 0; j + m <= i; j ++) {
            f[i] = min(f[i], f[j] + (psum[i] - psum[j]) * i - (tsum[i] - tsum[j]));
        }
    }
    int ans = inf;
    for (int i = t; i < t + m; i ++) ans = min(ans, f[i]);
    cout << ans << endl; 
    return 0;
}

时间复杂度：$O(t)$

再是这个式子
$$f_i=min(f_j+\sum _{j<tk\le i}i-t_k)$$
可以发现这个东西和斜率优化的基本套路是一样的。
那么稍微推导一下
将前缀和的式子拿出来$f_i=f_j+(psu{m}_i-psu{m}_j)\times i-(tsu{m}_i-tsu{m}_j)$
把和$i$有关的项都放到一边，把其他的$j$和$k$的项放到另外一边。
最终可以化简为
$${\underline{f_j+tsu{m}_j}}_y={\underline{i}}_k\times {\underline{psu{m}_i}}_x+{\underline{(f_i+psu{m}_j\times i-tsu{m}_i)}}_b$$

对应下面这个东西
$$y=kx+b$$

开始斜率优化。
可以发现斜率$i$递增，然后维护下凸包。

#include 
using namespace std;
namespace IOstream {
    #define gc getchar
    template <typename T>
    inline void read(T &x) {
        x = 0; T fl = 1; char c = 0;
        for (; c < '0' || c > '9'; c = gc()) if (c == '-') fl = -1;
        for (; c >= '0' && c <= '9'; c = gc()) x = (x << 1) + (x << 3) + (c ^ 48);
        x *= fl;
    }
    #undef gc
} using namespace IOstream;
typedef double db;
const int N = 4e6 + 506;
const int inf = 0x3f3f3f3f;
int psum[N], tsum[N], f[N], q[N << 1]; 
// psum记录的是人数前缀和，tsum表示总时间的前缀和
int n, m, T;
db Y(int i) { return 1.0 * (- f[i] - tsum[i]); }
db X(int i) { return 1.0 * (- psum[i]); }
db slope(int i, int j) { return (Y(i) - Y(j)) / (psum[i] == psum[j] ? 1e-9 : (X(i) - X(j))); }
int main() {
    read(n); read(m);
    if (m == 1) { puts("0"); return 0; }
    for (int i = 1, x; i <= n; i ++) {
        read(x); T = max(x, T);
        psum[x] ++; tsum[x] += x;
    }
    for (int i = 0; i < T + m; i ++) {
        tsum[i] += tsum[i - 1]; 
        psum[i] += psum[i - 1];
    }
    int h = 1, t = 0; 
    for (int i = 0; i < T + m; i ++) {
        if (i >= m) {
            while (h < t && slope(q[t - 1], q[t]) >= slope(q[t], i - m)) t --;
            q[++ t] = i - m; 
        }
        while (h < t && slope(q[h], q[h + 1]) <= i) h ++; 
        f[i] = psum[i] * i - tsum[i];
        int j = q[h];
        if (h <= t) f[i] = min(f[i], f[j] + (psum[i] - psum[j]) * i - (tsum[i] - tsum[j])); 
    }
    int ans = inf;
    for (int i = T; i < T + m; i ++) ans = min(ans, f[i]);
    cout << ans << endl; 
    return 0;
}