论文笔记Revisiting the Sibling Head in Object Detector

1. 论文标题及来源

Revisiting the Sibling Head in Object Detector, CVPR, 2020
下载地址：https://arxiv.org/abs/2003.07540

2. 拟解决问题

分类和回归的过程中特征不对齐问题，如下图所示(颜色越暖越好)

即当使用同一个特征进行分类和回归时，它的性能不能很好地得到平衡

3. 解决方法

3.1 算法流程

a. 将图片输入骨干网络提取特征
b. 通过RPN得到响应图
c. 通过Sibling head生成proposal
d. 将生成的每个proposal输入到Spatial distanglement模块分别得到用于分类的proposal和用于回归的proposal，即每个proposal会生成两个proposal，一个用于分类，另一个用于回归
e. 将用于分类的propostal输入分类分支得到分类得分；将用于回归的proposal输入回归分支得到回归偏移
f. 通过nms得到最终结果

3.2 task-aware空间解耦模块

如上图b所示，将proposal的ROI特征输入到上图b中，然后使用一个3层的全连接网络生成两个proposal，一个用于分类，一个用于回归。该模块通过下述公式学习相应的特征偏移。
$\Delta R=\gamma F_r(F;{\theta }_r)\cdot (w,h)$
$\stackrel{⌢}{P_r}=P+\Delta R$
通过上述公式生成用于回归的progosal，$\gamma$是一个超参数，用于控制贡献程度，$\Delta R\in R^{1\times 1\times 2}$

$\Delta C=\gamma F_c(F;{\theta }_c)\cdot (w,h)$
$${\stackrel{⌢}{F}}_c(x,y)=\sum _{p\in G(x,y)}\frac{F_B(p_0+\Delta C(x,y,1),p1+\Delta C(x,y,2))}{|G(x,y)|}$$
通过上述公式生成分类的特征偏移，然后通过线性插值获得用于分类的proposal，$\Delta C\in R^{k\times k\times 2}$，$G(x,y)$响应图上坐标为(x, y)的锚点(anchor)，$|G(x,y)|$表示采样的总锚点数，$(p_x,p_y)$表示采样点在网格G(x, y)的坐标，$F_B$表示线性插值函数

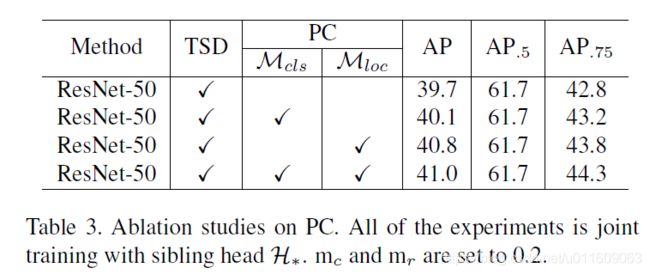
3.3 渐进式约束

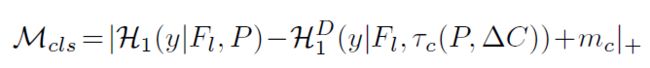
$H_1(y|\cdot )$表示类别y的得分，$|\cdot {|}_{+}$类似于Relu方式。

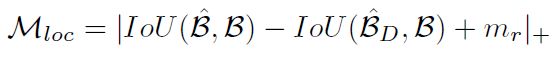
4. 实验结果

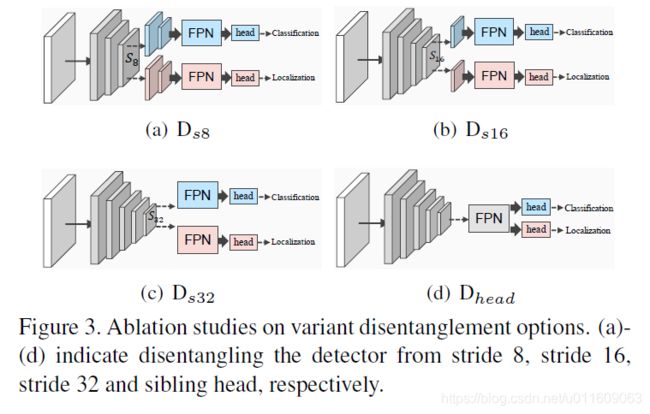
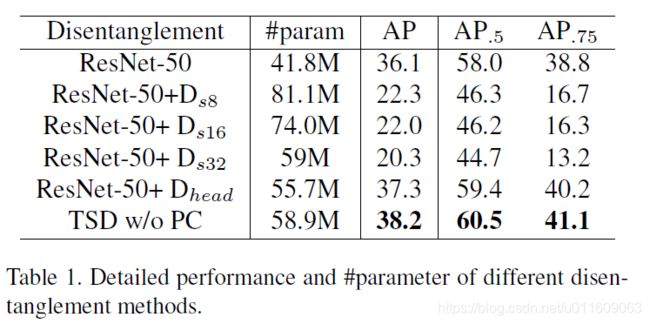
4.1 消融实验

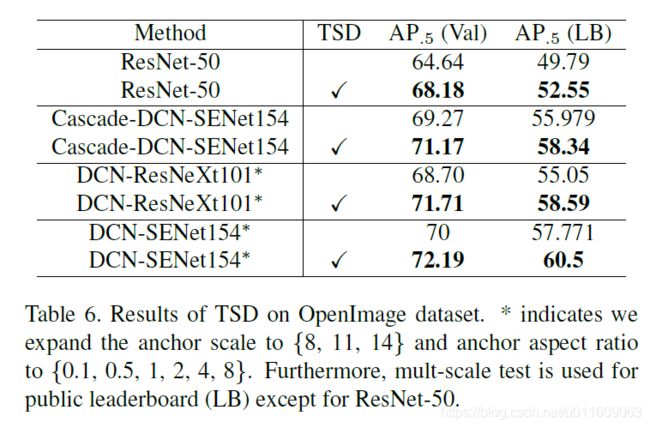
4.2 OpenImage实验结果

4.3 COCO实验结果

5. 总结

该算法通过实验发现分类和回归任务使用的特征不一样，提出使用解耦操作分别处理分类和回归，即通过一个原始的proposal生成两个proposal，一个用于分类，另一个用于回归，使它们能生成各自需要的特征，通过渐进性约束进一步提升算法性能。