IMU模型与标定
文章目录
- IMU传感器
- 旋转运动学
- 测量模型与运动模型
- MEMS加速度计
- 陀螺仪
- IMU误差模型
- 确定性误差
- 确定性误差标定方法——六面法
- 温度相关
- 随机误差
- 随机误差的标定方法——Allan方差法
- 数学模型
- 加速度计
- 陀螺仪
- VIO中模型
- 运动模型
- 离散积分方法
- 欧拉法
- 中值法(mid-point)
- 四阶龙格库塔(RK4)
- 总的标定流程
IMU传感器
旋转运动学
旋转的线速度为:
r ˙ = ( − a θ ˙ sin θ , a θ ˙ cos θ , 0 ) ⊤ = [ 0 − θ ˙ 0 θ ˙ 0 0 0 0 0 ] [ a cos θ a sin θ h ] = ω × r (1) \begin{aligned} \dot{\mathbf{r}} &=(-a \dot{\theta} \sin \theta, a \dot{\theta} \cos \theta, 0)^{\top} \\ &=\left[\begin{array}{ccc}{0} & {-\dot{\theta}} & {0} \\ {\dot{\theta}} & {0} & {0} \\ {0} & {0} & {0}\end{array}\right]\left[\begin{array}{c}{a \cos \theta} \\ {a \sin \theta} \\ {h}\end{array}\right] \\ &=\boldsymbol{\omega} \times \mathbf{r} \end{aligned} \tag{1} r˙=(−aθ˙sinθ,aθ˙cosθ,0)⊤=⎣⎡0θ˙0−θ˙00000⎦⎤⎣⎡acosθasinθh⎦⎤=ω×r(1)
取模得到角速度和线速度之间的关系:
∣ r ˙ ∣ = ∣ ω ∣ ∣ r ∣ sin ϕ = a ∣ θ ˙ ∣ (2) |\dot{\mathbf{r}}|=|\boldsymbol{\omega}||\mathbf{r}| \sin \phi=a|\dot{\theta}| \tag{2} ∣r˙∣=∣ω∣∣r∣sinϕ=a∣θ˙∣(2)
从Body系和Inertial系分别看旋转运动得到的速度关系为:
r ˙ I = R I B r ˙ B + R ˙ I B r B = R I B r ˙ B + [ R I B ω b ] × r = R I B v b + ω × r (3) \begin{aligned} \dot{\mathbf{r}}_{I} &=\mathbf{R}_{I B} \dot{\mathbf{r}}_{B}+\dot{\mathbf{R}}_{I B} \mathbf{r}_{B} \\ &=\mathbf{R}_{I B} \dot{\mathbf{r}}_{B}+\left[\mathbf{R}_{I B} \boldsymbol{\omega}_{b}\right]_{ \times} \mathbf{r} \\ &=\mathbf{R}_{I B} \mathbf{v}_{b}+\boldsymbol{\omega} \times \mathbf{r} \end{aligned} \tag{3} r˙I=RIBr˙B+R˙IBrB=RIBr˙B+[RIBωb]×r=RIBvb+ω×r(3)
v I ≡ R I B v b + ω × r ⇔ R I B v b ≡ v I − ω × r (4) \mathbf{v}_{I} \equiv \mathbf{R}_{I B} \mathbf{v}_{b}+\omega \times \mathbf{r} \Leftrightarrow \mathbf{R}_{I B} \mathbf{v}_{b} \equiv \mathbf{v}_{I}-\boldsymbol{\omega} \times \mathbf{r} \tag{4} vI≡RIBvb+ω×r⇔RIBvb≡vI−ω×r(4)
对公式(3)中速度求导得到加速度:
r ¨ I = R I B v ˙ B + R ˙ I B v B + ω × r ˙ + [ R ˙ I B ω b + R I B ω ˙ b ] × r = R I B a B + 2 ω × v + ω × ( ω × r ) + ω ˙ × r (5) \begin{aligned} \ddot{\mathbf{r}}_{I} &=\mathbf{R}_{I B} \dot{\mathbf{v}}_{B}+\dot{\mathbf{R}}_{I B} \mathbf{v}_{B}+\boldsymbol{\omega} \times \dot{\mathbf{r}}+\left[\dot{\mathbf{R}}_{I B} \boldsymbol{\omega}_{b}+\mathbf{R}_{I B} \dot{\boldsymbol{\omega}}_{b}\right]_{ \times} \mathbf{r} \\ &=\mathbf{R}_{I B} \mathbf{a}_{B}+2 \boldsymbol{\omega} \times \mathbf{v}+\boldsymbol{\omega} \times(\boldsymbol{\omega} \times \mathbf{r})+\dot{\boldsymbol{\omega}} \times \mathbf{r} \end{aligned} \tag{5} r¨I=RIBv˙B+R˙IBvB+ω×r˙+[R˙IBωb+RIBω˙b]×r=RIBaB+2ω×v+ω×(ω×r)+ω˙×r(5)
对公式(5)进行变形得到:
a = a I − 2 ω × v ⏟ 科 氏 力 − ω ˙ × r ⏟ 欧 拉 力 − ω × ( ω × r ) ⏟ 离 心 力 (6) \mathbf{a}=\mathbf{a}_{I}-\underbrace{2 \boldsymbol{\omega} \times \mathbf{v}}_{\text 科氏力}- \underbrace{\dot{\boldsymbol{\omega}} \times \mathbf{r}}_{\text 欧拉力}- \underbrace{\boldsymbol{\omega} \times(\boldsymbol{\omega} \times \mathbf{r})}_{\text 离心力} \tag{6} a=aI−科氏力 2ω×v−欧拉力 ω˙×r−离心力 ω×(ω×r)(6)
其中: v = R I B v b \mathbf{v}=\mathbf{R}_{I B} \mathbf{v}_{b} v=RIBvb, a = R I B a b \mathbf{a}=\mathbf{R}_{I B} \mathbf{a}_{b} a=RIBab,它们表示body下的速度或加速度在Inertial系下的表示。要区别这几种表示,习惯了找一个真实值,只不过是不同系下的不同表示罢了
测量模型与运动模型
MEMS加速度计
使用电容或者电阻桥来进行测量,注意有可能测出来的加速度计值方向是与实际力相反的,因为是使用弹簧测出的惯性力。
- 加速度计的质量块没有高速运动,不受科氏力影响
陀螺仪
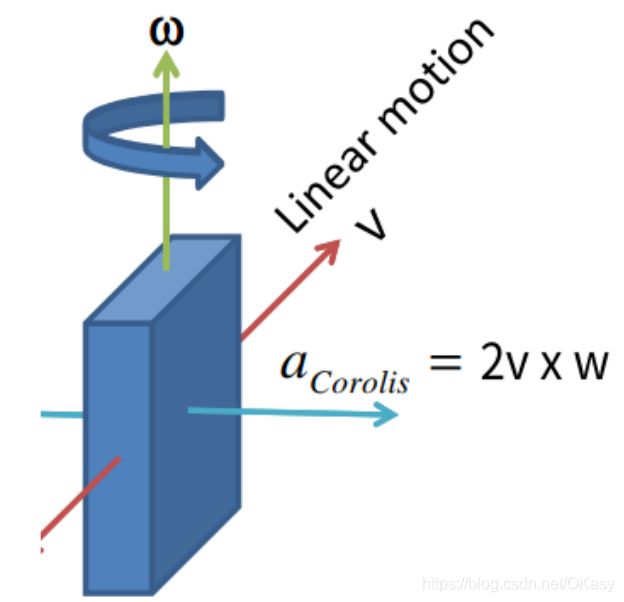
- 振动陀螺仪使用的是科氏力作用来测得旋转,一个主运动轴+一个敏感轴,与运动方向垂直方向(敏感轴方向)受一个科氏力。
- 一般使用两个运动方向相反的质量块来侧科氏力,这样可以抵消加速度的影响。若质量不一致会导致有差别。
IMU误差模型
分为:确定性误差,随机误差。前者可以提前标定,后者建模成高斯分布。
确定性误差
- 偏差bias
- 尺度因子Scale
- 轴偏差(非正交误差)
- Run-to-Run Bias/Scale Factor 即每次上电启动的值都不一样
- In Run (Stability) Bias/Scale Factor 即在运行过程中也会发生变化
- Temperature-Dependent Bias/Scale Factor 即受温度影响的变化值
尺度因子和非对称误差为:
[ l a x l a y l a z ] = [ s x x m x y m x z m y x s y y m y z m z x m z y s z z ] [ a x a y a z ] (7) \left[\begin{array}{l}{l_{a x}} \\ {l_{a y}} \\ {l_{a z}}\end{array}\right]=\left[\begin{array}{lll}{s_{x x}} & {m_{x y}} & {m_{x z}} \\ {m_{y x}} & {s_{y y}} & {m_{y z}} \\ {m_{z x}} & {m_{z y}} & {s_{z z}}\end{array}\right]\left[\begin{array}{c}{a_{x}} \\ {a_{y}} \\ {a_{z}}\end{array}\right] \tag{7} ⎣⎡laxlaylaz⎦⎤=⎣⎡sxxmyxmzxmxysyymzymxzmyzszz⎦⎤⎣⎡axayaz⎦⎤(7)
确定性误差标定方法——六面法
对于加速度计;
三轴分别朝上朝下放置一段时间,如果考虑为都是正交的,相加相减就可以得到:
b = l f u p + l f d o w n 2 S = l f u p − l f d o w n 2 ⋅ g (8) \begin{aligned} b &=\frac{l_{f}^{u p}+l_{f}^{d o w n}}{2} \\ S &=\frac{l_{f}^{u p}-l_{f}^{d o w n}}{2 \cdot g} \end{aligned} \tag{8} bS=2lfup+lfdown=2⋅glfup−lfdown(8)
考虑轴间误差时,实际值与测量值之间的关系为
[ l a x l a y l a z ] = [ s x x m x y m x z m y x s y y m y z m z x m z y s z z ] [ a x a y a z ] + [ b a x b a y b a z ] (9) \left[\begin{array}{l}{l_{a x}} \\ {l_{a y}} \\ {l_{a z}}\end{array}\right]=\left[\begin{array}{lll}{s_{x x}} & {m_{x y}} & {m_{x z}} \\ {m_{y x}} & {s_{y y}} & {m_{y z}} \\ {m_{z x}} & {m_{z y}} & {s_{z z}}\end{array}\right]\left[\begin{array}{c}{a_{x}} \\ {a_{y}} \\ {a_{z}}\end{array}\right]+\left[\begin{array}{c}{b_{a x}} \\ {b_{a y}} \\ {b_{a z}}\end{array}\right] \tag{9} ⎣⎡laxlaylaz⎦⎤=⎣⎡sxxmyxmzxmxysyymzymxzmyzszz⎦⎤⎣⎡axayaz⎦⎤+⎣⎡baxbaybaz⎦⎤(9)
变为齐次坐标得到:
[ l a x l a y l a z ] = [ s x x m x y m x z b a x m y x s y y m y z b a y m z x m z y s z z b a z ] [ a x a y a z 1 ] (10) \left[\begin{array}{l}{l_{a x}} \\ {l_{a y}} \\ {l_{a z}}\end{array}\right]=\left[\begin{array}{lll}{s_{x x}} & {m_{x y}} & {m_{x z}} &{b_{a x}} \\ {m_{y x}} & {s_{y y}} & {m_{y z}} &{b_{a y}} \\ {m_{z x}} & {m_{z y}} & {s_{z z}} &{b_{a z}}\end{array}\right]\left[\begin{array}{c}{a_{x}} \\ {a_{y}} \\ {a_{z}} \\ 1\end{array}\right] \tag{10} ⎣⎡laxlaylaz⎦⎤=⎣⎡sxxmyxmzxmxysyymzymxzmyzszzbaxbaybaz⎦⎤⎣⎢⎢⎡axayaz1⎦⎥⎥⎤(10)
然后再进行转置,标准的加速度值已知,利用最小二乘求解12个参数即可。
对于陀螺仪;
也可以使用六面法,需要高精度转台提供真实值,六个值分别为绕各个轴的顺时针和逆时针的角速度。
温度相关
进行温度补偿,获得不同温度时的bias和scale值,绘制成曲线。
- soak 方法:控制不同的恒温值,测得传感器数据。
- ramp 方法:记录一段时间内线性升温和降温时传感器数据。
随机误差
高斯白噪声建模成均值为0,方差 σ \sigma σ的各时刻独立的高斯过程,一般是由AD转换器引起的外部噪声。
E [ n ( t ) ] ≡ 0 E [ n ( t 1 ) n ( t 2 ) ] = σ 2 δ ( t 1 − t 2 ) (11) \begin{array}{l}{E[n(t)] \equiv 0} \\ {E\left[n\left(t_{1}\right) n\left(t_{2}\right)\right]=\sigma^{2} \delta\left(t_{1}-t_{2}\right)}\end{array} \tag{11} E[n(t)]≡0E[n(t1)n(t2)]=σ2δ(t1−t2)(11)
其中 δ ( ) \delta() δ()表示狄拉克函数。
离散的数据噪声,与连续的高斯白噪声方差之间的转换关系为:
n d [ k ] ≜ n ( t 0 + Δ t ) ≃ 1 Δ t ∫ t 0 t 0 + Δ t n ( τ ) d t E ( n d [ k ] 2 ) = E ( 1 Δ t 2 ∫ t 0 t 0 + Δ t ∫ t 0 t 0 + Δ t n ( τ ) n ( t ) d τ d t ) = E ( σ 2 Δ t 2 ∫ t 0 t 0 + Δ t ∫ t 0 t 0 + Δ t δ ( t − τ ) d τ d t ) = E ( σ 2 Δ t ) (12) n_{d}[k] \triangleq n\left(t_{0}+\Delta t\right) \simeq \frac{1}{\Delta t} \int_{t_{0}}^{t_{0}+\Delta t} n(\tau) d t \\\begin{aligned} E\left(n_{d}[k]^{2}\right) &=E\left(\frac{1}{\Delta t^{2}} \int_{t_{0}}^{t_{0}+\Delta t} \int_{t_{0}}^{t_{0}+\Delta t} n(\tau) n(t) d \tau d t\right) \\ &=E\left(\frac{\sigma^{2}}{\Delta t^{2}} \int_{t_{0}}^{t_{0}+\Delta t} \int_{t_{0}}^{t_{0}+\Delta t} \delta(t-\tau) d \tau d t\right) \\ &=E\left(\frac{\sigma^{2}}{\Delta t}\right) \end{aligned} \tag{12} nd[k]≜n(t0+Δt)≃Δt1∫t0t0+Δtn(τ)dtE(nd[k]2)=E(Δt21∫t0t0+Δt∫t0t0+Δtn(τ)n(t)dτdt)=E(Δt2σ2∫t0t0+Δt∫t0t0+Δtδ(t−τ)dτdt)=E(Δtσ2)(12)
所以离散的高斯白噪声为:
n d [ k ] = σ d w [ k ] (13) n_{d}[k]=\sigma_{d} w[k] \tag{13} nd[k]=σdw[k](13)
其中: w [ k ] ∼ N ( 0 , 1 ) w[k] \sim \mathcal{N}(0,1) w[k]∼N(0,1), σ d = σ 1 Δ t \sigma_{d}=\sigma \frac{1}{\sqrt{\Delta t}} σd=σΔt1
随机游走可以把它看做是一种布朗运动,或者将其称之为维纳过程。该模型可以看做是高斯白噪声的积分。该噪声参数一般是由传感器的内部构造、温度等变化量综合影响下的结果。建模成导数为高斯分布的噪声。
b ˙ ( t ) = n ( t ) = σ b w ( t ) (14) \dot{b}(t)=n(t)=\sigma_{b} w(t) \tag{14} b˙(t)=n(t)=σbw(t)(14)
同样离散的和连续的之间转换为:
b d [ k ] ≜ b ( t 0 ) + ∫ t 0 t 0 + Δ t n ( t ) d t E ( ( b d [ k ] − b d [ k − 1 ] 2 ) = E ( ∫ t 0 t 0 + Δ t ∫ t 0 t 0 + Δ t n ( t ) n ( τ ) d τ d t ) = E ( σ b 2 ∫ t 0 t 0 + Δ t ∫ t 0 t 0 + Δ t δ ( t − τ ) d τ d t ) = E ( σ b 2 Δ t ) (15) \begin{aligned} b_{d}[k] \triangleq & b\left(t_{0}\right)+\int_{t_{0}}^{t_{0}+\Delta t} n(t) d t \\ E\left(\left(b_{d}[k]-b_{d}[k-1]^{2}\right)\right.&=E\left(\int_{t_{0}}^{t_{0}+\Delta t} \int_{t_{0}}^{t_{0}+\Delta t} n(t) n(\tau) d \tau d t\right) \\ &=E\left(\sigma_{b}^{2} \int_{t_{0}}^{t_{0}+\Delta t} \int_{t_{0}}^{t_{0}+\Delta t} \delta(t-\tau) d \tau d t\right) \\ &=E\left(\sigma_{b}^{2} \Delta t\right) \end{aligned} \tag{15} bd[k]≜E((bd[k]−bd[k−1]2)b(t0)+∫t0t0+Δtn(t)dt=E(∫t0t0+Δt∫t0t0+Δtn(t)n(τ)dτdt)=E(σb2∫t0t0+Δt∫t0t0+Δtδ(t−τ)dτdt)=E(σb2Δt)(15)
即:
b d [ k ] = b d [ k − 1 ] + σ b d w [ k ] (16) b_{d}[k]=b_{d}[k-1]+\sigma_{b d} w[k] \tag{16} bd[k]=bd[k−1]+σbdw[k](16)
其中: w [ k ] ∼ N ( 0 , 1 ) w[k] \sim \mathcal{N}(0,1) w[k]∼N(0,1), σ b d = σ b Δ t \sigma_{b d}=\sigma_{b} \sqrt{\Delta t} σbd=σbΔt
随机误差的标定方法——Allan方差法
具体流程如下:
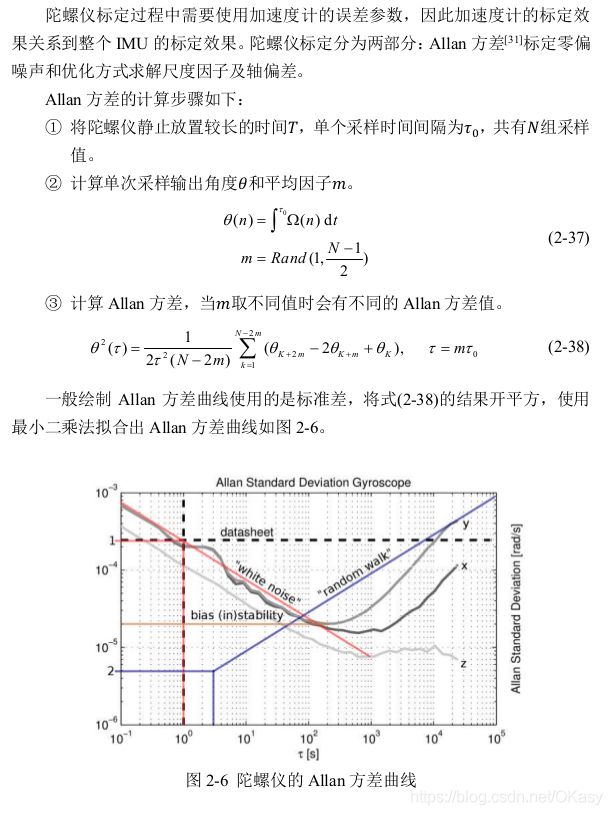
- 将陀螺仪静止放置时间 T T T ,单个采样周期为 τ 0 \tau_0 τ0 ,共有 N N N组采样值。
- 计算单次采样输出角度 θ \theta θ 和 平均因子 m m m, m m m要尽量取得均匀。
θ ( n ) = ∫ τ 0 Ω ( n ) d t m = Rand ( 1 , N − 1 2 ) (17) \begin{aligned} \theta(n) &=\int^{\tau_{0}} \Omega(n) d t \\ m &=\operatorname{Rand}\left(1, \frac{N-1}{2}\right) \end{aligned} \tag{17} θ(n)m=∫τ0Ω(n)dt=Rand(1,2N−1)(17)
- 计算Allan方差,当 m m m取不同的值的时候会有不同的Allan方差值。
θ 2 ( τ ) = 1 2 τ 2 ( N − 2 m ) ∑ k = 1 N − 2 m ( θ K + 2 m − 2 θ K + m + θ K ) 2 (18) \theta^{2}(\tau)=\frac{1}{2\tau^{2}(N-2m)} \sum^{N-2m}_{k=1}(\theta_{K+2m}-2\theta_{K+m}+\theta_{K})^2 \tag{18} θ2(τ)=2τ2(N−2m)1k=1∑N−2m(θK+2m−2θK+m+θK)2(18)
其中: τ = m τ 0 \tau=m \tau_{0} τ=mτ0
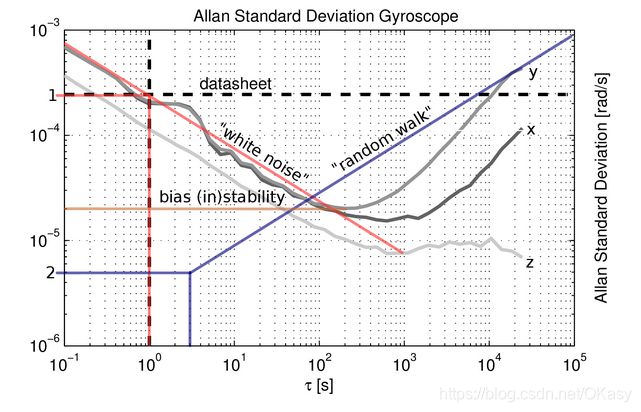
- 一般在绘制Allan方差曲线的时候使用的是Allan方差的平方根,将公式(18)开根号。
使用最小二乘对计算出来的Allan方差曲线进行拟合,得到如下的示意图。
按照上表中的值进行对应求得相应的噪声值,因为画出的曲线图是log-log对数图,因此斜率分别就是 τ \tau τ的次幂。
认为这些噪声源是相互独立的,则Allan方差是各类型误差的平方和:
σ total 2 ( τ ) = σ Q 2 ( τ ) + σ N 2 ( τ ) + σ B 2 ( τ ) + σ K 2 ( τ ) + σ R 2 ( τ ) = 3 Q 2 τ 2 + N 2 τ + 2 B 2 π ln 2 + K 2 τ 3 + R 2 τ 2 2 (19) \begin{aligned} \sigma_{\text { total }}^{2}(\tau) &=\sigma_{Q}^{2}(\tau)+\sigma_{N}^{2}(\tau)+\sigma_{B}^{2}(\tau)+\sigma_{K}^{2}(\tau)+\sigma_{R}^{2}(\tau) \\ &=\frac{3 Q^{2}}{\tau^{2}}+\frac{N^{2}}{\tau}+\frac{2 B^{2}}{\pi} \ln 2+\frac{K^{2} \tau}{3}+\frac{R^{2} \tau^{2}}{2} \end{aligned} \tag{19} σ total 2(τ)=σQ2(τ)+σN2(τ)+σB2(τ)+σK2(τ)+σR2(τ)=τ23Q2+τN2+π2B2ln2+3K2τ+2R2τ2(19)
把公式(19)整理下:
σ t o t a l 2 ( τ ) = ∑ i = − 2 2 C i τ i (20) \sigma_{\mathrm{total}}^{2}(\tau)=\sum_{i=-2}^{2} C_{i} \tau^{i} \tag{20} σtotal2(τ)=i=−2∑2Ciτi(20)
其中: i = ( − 2 , − 1 , 0 , 1 , 2 ) i=(-2,-1,0,1,2) i=(−2,−1,0,1,2)
使用最小二乘方法对公式(20)与公式(18)计算出来的值进行拟合,得到 C i C_i Ci值,然后得到相应的误差系数:
{ Q = C − 2 3600 3 ( ∘ ) N = C − 1 60 ( ∘ ) / h B = C 0 0.664 ( ∘ ) / h K = 60 3 C 1 [ ( ∘ ) ⋅ h − 1 ] / h R = 3600 2 C 2 [ ( ∘ ) ⋅ h − 1 ] / h (21) \left\{\begin{array}{l}{Q=\frac{\sqrt{C_{-2}}}{3600 \sqrt{3}}\left(^{\circ}\right)} \\ {N=\frac{\sqrt{C_{-1}}}{60}\left(^{\circ}\right) / \sqrt{h}} \\ {B=\frac{\sqrt{C_{0}}}{0.664}\left(^{\circ}\right) / h} \\ {K=60 \sqrt{3 C_{1}}\left[\left(^{\circ}\right) \cdot h^{-1}\right] / \sqrt{h}} \\ {R=3600 \sqrt{2 C_{2}}\left[\left(^{\circ}\right) \cdot h^{-1}\right] / h}\end{array}\right. \tag{21} ⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧Q=36003C−2(∘)N=60C−1(∘)/hB=0.664C0(∘)/hK=603C1[(∘)⋅h−1]/hR=36002C2[(∘)⋅h−1]/h(21)
其中陀螺仪的数据数据转为 deg/h, τ \tau τ还是sec单位,加速度计还是m/s2 。
imu_utils其中就是使用ceres求解最小二乘得到相应的系数,公式(18)到公式(21)的过程,注意其中的单位转换。
有一点不明白的是这几个误差系数是单独作用在每一段么?代码中测试发现就是令 τ \tau τ就是求得值。画出来的就是总的Allan方差曲线,为什么拟合出来可以单独代表其中一部分的噪声?公式(19)怎么获得单独的噪声?
找到一种解释:1s 量级的平均时间范围内加速度计的误差主要是速度随机游走, 在 100s 以上的范围内主要是零偏不稳定性. 对于更长的平均时间而言, 限于采集数据的长度, 用于 Allan 方差分析的独立子集个数有限, 因此其置信程度很低。
也就是说它确实是分段的,因此可以直接拟合得到。试了下为什么可以直接赋值1计算,是因为其他的太小了,忽略不计。因为次幂的不同,因此取不同时间时,噪声的大小差别很大,因此就直接忽略了,因此可以看做分段的。
数学模型
加速度计
a m B = S a T a R B G ( a G − g G ) + n a + b a (22) \mathbf{a}_{m}^{B}=\mathbf{S}_{a}\mathbf{T}_{a} \mathbf{R}_{B G}\left(\mathbf{a}^{G}-\mathbf{g}^{G}\right)+\mathbf{n}_{a}+\mathbf{b}_{a} \tag{22} amB=SaTaRBG(aG−gG)+na+ba(22)
陀螺仪
ω m B = S g T g ω B + s g a a B + n g + b g (23) \boldsymbol{\omega}_{m}^{B}=\mathbf{S}_{g} \mathbf{T}_{g}\boldsymbol{\omega}^{B}+\mathbf{s}_{g a} \mathbf{a}^{B}+\mathbf{n}_{g}+\mathbf{b}_{g} \tag{23} ωmB=SgTgωB+sgaaB+ng+bg(23)
S \mathbf S S是尺度因子, T \mathbf T T是非对称误差, n \mathbf n n是高斯白噪声, b \mathbf b b是零偏随机游走, s g a \mathbf{s}_{g a} sga是加速度计对陀螺仪的影响。
VIO中模型
VIO中忽略尺度因子和轴偏差,只考虑白噪声和bias随机游走。
ω ~ b = ω b + b g + n g a ~ b = q b w ( a w + g w ) + b a + n a (24) \begin{aligned} \tilde{\omega}^{b} &=\omega^{b}+\mathbf{b}^{g}+\mathbf{n}^{g} \\ \tilde{\mathbf{a}}^{b} &=\mathbf{q}_{b w}\left(\mathbf{a}^{w}+\mathbf{g}^{w}\right)+\mathbf{b}^{a}+\mathbf{n}^{a} \end{aligned} \tag{24} ω~ba~b=ωb+bg+ng=qbw(aw+gw)+ba+na(24)
这里的** g g g加号减号**注意就行了,和 g g g定义的正负,加速度计输出的加速度正负都有关系。
运动模型
参考预积分或者VINS的笔记就好了。
离散积分方法
p w b k + 1 = p w b k + v k w Δ t + 1 2 a Δ t 2 v k + 1 w = v k w + a Δ t q w b k + 1 = q w b k ⊗ [ 1 1 2 ω δ t ] (25) \begin{aligned}\mathbf{p}_{w b_{k+1}}&=\mathbf{p}_{w b_{k}}+\mathbf{v}_{k}^{w} \Delta t+\frac{1}{2} \mathbf{a} \Delta t^{2} \\ \mathbf{v}_{k+1}^{w}&=\mathbf{v}_{k}^{w}+\mathbf{a} \Delta t \\ \mathbf{q}_{w b_{k+1}}&=\mathbf{q}_{w b_{k}} \otimes\left[\begin{array}{c}{1} \\ {\frac{1}{2} \omega \delta t}\end{array}\right]\end{aligned} \tag{25} pwbk+1vk+1wqwbk+1=pwbk+vkwΔt+21aΔt2=vkw+aΔt=qwbk⊗[121ωδt](25)
对于非线性函数有以下的方法。
欧拉法
X n + 1 = X n + K Δ t K = f ′ ( t n , X n ) (26) \mathbf X_{n+1} =\mathbf X_{n} + \mathrm K\Delta t\\ K=f'(t_{n},\ \mathbf X_n) \tag{26} Xn+1=Xn+KΔtK=f′(tn, Xn)(26)
其中公式(24)中
a = q w b k ( a b k − b k a ) − g w ω = ω b k − b k g \begin{aligned} \mathbf{a} &=\mathbf{q}_{w b_{k}}\left(\mathbf{a}^{b_{k}}-\mathbf{b}_{k}^{a}\right)-\mathbf{g}^{w} \\ \boldsymbol{\omega} &=\boldsymbol{\omega}^{b_{k}}-\mathbf{b}_{k}^{g} \end{aligned} aω=qwbk(abk−bka)−gw=ωbk−bkg
中值法(mid-point)
X n + 1 = X n + K 2 Δ t K 2 = f ′ ( t n + 1 2 Δ t , X n + K 1 Δ t 2 ) K 1 = f ′ ( t n , X n ) (27) \begin{aligned} \mathbf X_{n+1} &= \mathbf X_{n}+\mathrm K_2\Delta t \\ \mathrm K_2 &= f'(t_n+\frac{1}{2}\Delta t, \ \mathbf X_n+\mathrm K_1\frac{\Delta t}{2} ) \\ \mathrm K_1 &=f'(t_n, \ \mathbf X_n) \end{aligned} \tag{27} Xn+1K2K1=Xn+K2Δt=f′(tn+21Δt, Xn+K12Δt)=f′(tn, Xn)(27)
其中公式(24)中的
a = 1 2 [ q w b k ( a b k − b k a ) − g w + q w b k + 1 ( a b k + 1 − b k a ) − g w ] ω = 1 2 [ ( ω b k − b k g ) + ( ω b k + 1 − b k g ) ] \begin{aligned} \mathbf{a} &=\frac{1}{2}\left[\mathbf{q}_{w b_{k}}\left(\mathbf{a}^{b_{k}}-\mathbf{b}_{k}^{a}\right)-\mathbf{g}^{w}+\mathbf{q}_{w b_{k+1}}\left(\mathbf{a}^{b_{k+1}}-\mathbf{b}_{k}^{a}\right)-\mathbf{g}^{w}\right] \\ \boldsymbol{\omega} &=\frac{1}{2}\left[\left(\boldsymbol{\omega}^{b_{k}}-\mathbf{b}_{k}^{g}\right)+\left(\boldsymbol{\omega}^{b_{k+1}}-\mathbf{b}_{k}^{g}\right)\right] \end{aligned} aω=21[qwbk(abk−bka)−gw+qwbk+1(abk+1−bka)−gw]=21[(ωbk−bkg)+(ωbk+1−bkg)]
四阶龙格库塔(RK4)
龙格库塔法的微分方程中必须有原来的量,即 y ˙ = f ( t , y ) \dot y=f(t,y) y˙=f(t,y)形式才适用。
X n + 1 = X n + Δ t 6 ( K 1 + 2 K 2 + 2 K 3 + K 4 ) K 1 = f ′ ( t n , X n ) K 2 = f ′ ( t n + Δ t 2 , X n + Δ t 2 K 1 ) K 3 = f ′ ( t n + Δ t 2 , X n + Δ t 2 K 2 ) K 4 = f ′ ( t n + Δ t , X n + Δ t K 3 ) (28) \begin{aligned} \mathbf X_{n+1} &= \mathbf X_{n}+\frac{\Delta t}{6}(\mathrm{K_1+2K_2+2K_3+K_4}) \\ \mathrm K_1 &=f'(t_n, \ \mathbf X_n) \\ \mathrm K_2 &=f'(t_n+\frac{\Delta t}{2}, \ \mathbf X_n +\frac{\Delta t}{2} \mathrm K_1) \\ \mathrm K_3 &= f'(t_n+\frac{\Delta t}{2}, \ \mathbf X_n +\frac{\Delta t}{2} \mathrm K_2) \\ \mathrm K_4 &= f'(t_n+\Delta t, \ \mathbf X_n +{\Delta t} \mathrm K_3) \\ \end{aligned} \tag{28} Xn+1K1K2K3K4=Xn+6Δt(K1+2K2+2K3+K4)=f′(tn, Xn)=f′(tn+2Δt, Xn+2ΔtK1)=f′(tn+2Δt, Xn+2ΔtK2)=f′(tn+Δt, Xn+ΔtK3)(28)
其中公式(24)中的
a = 1 2 [ q w b k ( a b k − b k a ) − g w + q w b k + 1 ( a b k + 1 − b k a ) − g w ] \begin{aligned} \mathbf{a} &=\frac{1}{2}\left[\mathbf{q}_{w b_{k}}\left(\mathbf{a}^{b_{k}}-\mathbf{b}_{k}^{a}\right)-\mathbf{g}^{w}+\mathbf{q}_{w b_{k+1}}\left(\mathbf{a}^{b_{k+1}}-\mathbf{b}_{k}^{a}\right)-\mathbf{g}^{w}\right] \end{aligned} a=21[qwbk(abk−bka)−gw+qwbk+1(abk+1−bka)−gw]
template
inline void imu_tk::quatIntegrationStepRK4(
const Eigen::Matrix< _T, 4, 1> &quat,
const Eigen::Matrix< _T, 3, 1> &omega0,
const Eigen::Matrix< _T, 3, 1> &omega1,
const _T &dt, Eigen::Matrix< _T, 4, 1> &quat_res )
{
Eigen::Matrix< _T, 3, 1> omega01 = _T(0.5)*( omega0 + omega1 );
Eigen::Matrix< _T, 4, 1> k1, k2, k3, k4, tmp_q;
Eigen::Matrix< _T, 4, 4> omega_skew;
// First Runge-Kutta coefficient
computeOmegaSkew( omega0, omega_skew );
k1 = _T(0.5)*omega_skew*quat;
// Second Runge-Kutta coefficient
tmp_q = quat + _T(0.5)*dt*k1;
computeOmegaSkew( omega01, omega_skew );
k2 = _T(0.5)*omega_skew*tmp_q;
// Third Runge-Kutta coefficient (same omega skew as second coeff.)
tmp_q = quat + _T(0.5)*dt*k2;
k3 = _T(0.5)*omega_skew*tmp_q;
// Forth Runge-Kutta coefficient
tmp_q = quat + dt*k3;
computeOmegaSkew( omega1, omega_skew );
k4 = _T(0.5)*omega_skew*tmp_q;
_T mult1 = _T(1.0)/_T(6.0), mult2 = _T(1.0)/_T(3.0);
quat_res = quat + dt*(mult1*k1 + mult2*k2 + mult2*k3 + mult1*k4);
normalizeQuaternion(quat_res);
}
总的标定流程
以IMU_tk为例,直接用本科毕设论文里的吧,有些符号可能不一样,比如考虑陀螺仪轴和加速度计轴不垂直、不重合的轴向误差。