第十章 k-均值算法 10.4 对地图上的点进行聚类

将地图上的点进行聚类，安排交通工具抵达这些簇的质心，然后步行到每个簇内地址。

这里我们直接用给出的文件进行操作，跳过10.4.1节。

添加代码：

def distSLC(vecA, vecB): # 返回地球表面两点之间的距离
    a = sin(vecA[0,1] * pi / 180) * sin(vecB[0,1] * pi / 180)
    b = cos(vecA[0,1] * pi / 180) * cos(vecB[0,1] * pi / 180) * \
                        cos(pi * (vecB[0,0] - vecA[0,0]) / 180)
    return arccos(a + b) * 6371.0

import matplotlib
import matplotlib.pyplot as plt
def clusterClubs(numClust = 5): # 画图，参数为希望得到的簇数目
    datList = []
    for line in open('places.txt').readlines():
        lineArr = line.split('\t')
        datList.append([float(lineArr[4]), float(lineArr[3])])
    datMat = mat(datList)
    myCentroids, clustAssing = biKmeans(datMat, numClust, \
                                        distMeas = distSLC)
    fig = plt.figure()
    rect = [0.1, 0.1, 0.8, 0.8]
    scatterMarkers = ['s', 'o', '^', '8', 'p', \
                      'd', 'v', 'h', '>', '<']
    axprops = dict(xticks = [], yticks = [])
    ax0 = fig.add_axes(rect, label = 'ax0', **axprops)
    imgP = plt.imread('Portland.png') # imread 基于图像创建矩阵
    ax0.imshow(imgP)
    ax1 = fig.add_axes(rect, label = 'ax1', frameon = False)
    for i in range(numClust):
            ptsInCurrCluster = datMat[nonzero(clustAssing[:,0].A == i)[0],:]
            markerStyle = scatterMarkers[i % len(scatterMarkers)] # 使用索引来选择标记形状
            ax1.scatter(ptsInCurrCluster[:,0].flatten().A[0],\
                        ptsInCurrCluster[:,1].flatten().A[0],\
                        marker = markerStyle, s = 90)
    ax1.scatter(myCentroids[:,0].flatten().A[0],\
                    myCentroids[:,1].flatten().A[0], marker = '+', s = 300)
    plt.show()

运行代码：

import kMeans
from numpy import *

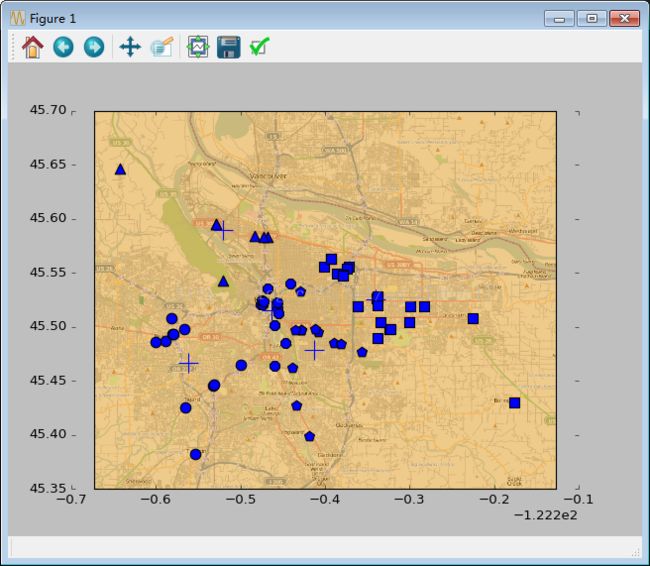
kMeans.clusterClubs(5)

得到结果：

==================================================================================

通过修改簇的数目，得到程序运行的效果。

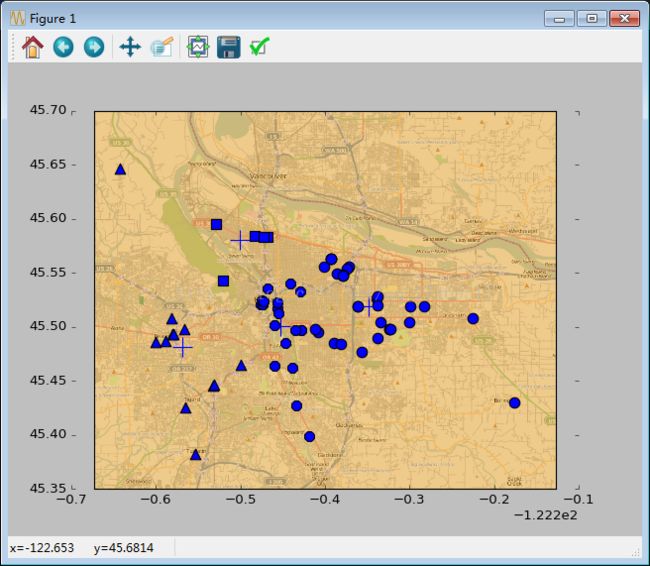
比如4簇：

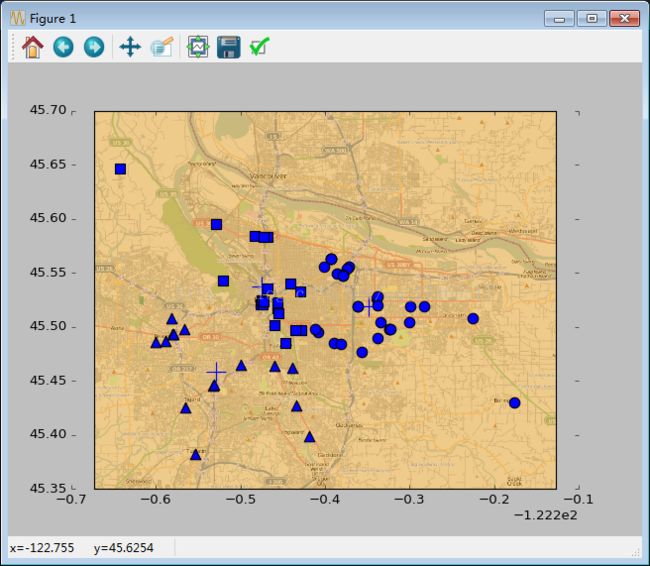
3簇：

================================================================================================

10.5 小结

聚类是一种无监督的学习方法。所谓无监督学习是指事先并不知道要寻找的内容，即没有目标变量。聚类将数据点归到多个簇中，其中相似数据点处于同一簇，而不相似数据点处于不同簇中。聚类中可以使用多种不同的方法计算相似度。

K-均值聚类算法以 k 个随机质心开始。算法会计算每个点到质心的距离。每个点会被分配到距其最近的簇质心。然后紧接着基于新分配到簇的点更新簇质心。以上过程重复数次，直到质心不再改变。

为了得到更好地聚类效果，可以使用另一种称为二分 k-均值 的聚类算法。该方法首先将所有点作为一个簇，然后使用 k-均值 算法对其划分，下一次迭代时，选择有最大误差的簇进行划分。这个过程重复直到 k 个簇创建为止。