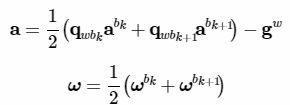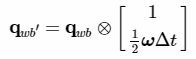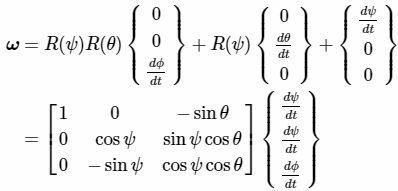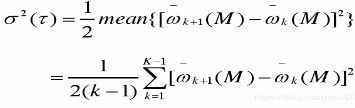IMU的数学模型与误差标定问题

IMU数学模型

加速度计

首先，对于世界坐标系，一般我们会使用最常见的东北天(ENU)坐标系G（无关远点位置，只与姿态有关）。

在这个坐标系中，重力加速度为

此时，假设IMU坐标系就是ENU坐标系，则，静止时有（其中是测量值）：

所以，不静止时：（此处对a和g符号不做区分标记，因为假设body系与Global系一样）

由上可知，其实在物体做自由落体时imu测量的加速度才是0，静止时反而是，这个是由加速度计的测量原理决定的。

上面讲的是在IMU坐标系也是ENU坐标系时的情况（此时位置无关，只关乎姿态）。大多数实际应用中，IMU坐标系（Body）一般是与ENU坐标系有一个姿态的变化的。此时，得到的理论测量值为：

此处是将Global坐标转换到Body坐标姿态的旋转矩阵。此处可以看出，global坐标系的位置与body坐标系的位置与在两个系下测量的加速度大小无关。但是，与姿态有关。

陀螺仪

相比较于加速度计，陀螺仪相对简单。如果不考虑误差，则

我们会发现此处并没有像加速度计一样，将global坐标系下的角速度转换到陀螺仪的测量值，而是直接使用body系下的角速度。这是因为旋转叠加时（比如四元数和旋转矩阵表示姿态时），全局姿态是直接乘以body系下的更新量的就可以得到新的全局姿态的。

恢复运动轨迹

imu最后输出的是一个离散的加速度、角速度序列。我们想做的是利用这些恢复出运动的轨迹（也就是一个位姿的序列）。

下面会介绍两种离散积分的方法。欧拉法与中值法。

这两种方法，都是已知了时刻的位姿，时刻与时刻的测量值（加速度与角速度）。目的是求得时刻的位姿。

欧拉法

欧拉法，是直接使用时刻的测量值来积分。

其中

中值法

中值法，使用两个相邻时刻到的位姿是用两个时刻的测量值的平均值来离散积分。

其中

代码

 for (int i = 0; i < imudata.size()-1; ++i) {

        MotionData imupose = imudata[i];
        MotionData imupose1 = imudata[i+1];
/*
        // 欧拉积分
        //delta_q = [1 , 1/2 * thetax , 1/2 * theta_y, 1/2 * theta_z]
        Eigen::Quaterniond dq;
        Eigen::Vector3d dtheta_half =  imupose.imu_gyro * dt /2.0;
        dq.w() = 1;
        dq.x() = dtheta_half.x();
        dq.y() = dtheta_half.y();
        dq.z() = dtheta_half.z();
        Eigen::Vector3d acc_w = Qwb * (imupose.imu_acc) + gw;
        Pwb = Pwb + Vw * dt + 0.5 * dt * dt * acc_w;
        Vw = acc_w * dt + Vw;
        Qwb = Qwb * dq;
        Qwb.normalize();
*/

        /// 中值积分
        Eigen::Quaterniond dq;
        Eigen::Vector3d dtheta_half = (imupose.imu_gyro + imupose1.imu_gyro)*dt/4.0;
        dq.w() = 1;
        dq.x() = dtheta_half.x();
        dq.y() = dtheta_half.y();
        dq.z() = dtheta_half.z();
        Eigen::Quaterniond Qwb1 = Qwb * dq;
        Qwb1.normalize();
        Eigen::Vector3d acc_w = (Qwb * imupose.imu_acc + Qwb1 * imupose1.imu_acc)*0.5 + gw;
        Pwb = Pwb + Vw * dt + 0.5 * dt * dt * acc_w;
        Vw = acc_w * dt + Vw;  
        Qwb = Qwb1;

        //存储位姿
        save_points<

此处推荐一个生成imu数据、加噪声与测试的工具，这里中值积分与欧拉积分可以参考上面的我的代码，因为工具里可能不一定提供了。

旋转积分

上面恢复姿态轨迹的积分用了四元数的形式，下面我想多介绍几个

此处是imu的测量结果，也就是局部角速度。因为这个旋转积分的结果是姿态，因此下面会分别介绍使用四元数、SO3还有欧拉角下的积分方式。

• 四元数的形式：

• 形式：

• 欧拉角形式：

我们可以发现，这三种方法，对于全局姿态的变化，旋转矩阵与四元数都是直接使用imu的测量（也就是局部角速度）进行更新的。只有在欧拉角的形式里，表示将IMU body坐标系下的角速度转化成欧拉角速度。此处可以推导出，这个是三种方法中唯一一个需要转换的地方。原因的话，我觉得这是因为累加与累乘的区别，欧拉角不支持乘法。如果使用角度来表示旋转矩阵与四元数，此时对角度的更新也得使用加法（原来角度加上角速度与时间的积即为新的角度），但是四元数与旋转矩阵本身是只支持乘法的，它们是直接乘以局部扰动即可。

欧拉角速度到imu输出角速度

这个挺有必要的，因为用欧拉角来表示姿态还是很方便的。

• step1:绕着惯性坐标系的z轴旋转，得到新的坐标系

• step2:绕着新坐标系的y轴旋转得到坐标系

• step3:绕着新坐标系的x轴旋转得到坐标系，就是我们的body坐标系

欧拉角速度到body角速度：

上面取逆就得到，如下body到欧拉角的变换：

误差与标定

加速度计和陀螺仪的误差可以分为确定性误差与随机误差。

确定性误差

确定性误差可以事先标定确定，包括：bias，scale …

bias

理论上，当没有外部作用时，IMU传感器的输出应该为0。但是，实际上数据存在一个偏置b。

scale

scale可以看成是实际数值和传感器输出值之间的比值。

Nonorthogonality/Misalignment Errors

在多轴IMU传感器制作的时候，由于制作工艺的问题的问题，会使得xyzxyz轴可能不垂直，这个也叫轴间误差。

轴间误差使得本来x轴的分量会对测量到的y轴与z轴的分量有影响。将其与scale误差相结合，会得到如下的测量与实际的对应关系。

其他确定性误差

bias与scale的误差是会受温度影响的，并且在运行中也许也会改变。

---

 

确定新误差的标定（六面法）

以加速度计为例，陀螺仪同理

指将加速度计的3个轴分别朝上或者朝下水平放置一段时间（对于陀螺仪就是在三个旋转轴上正反旋转，不过需要高精度转台），采集六个面的数据完成标定。

3个轴都是正交时

其中，为加速度计某个轴的测量值，为当地的重力加速度。

当具有轴间误差时

此时实际加速度和测量值之间的关系为：

水平静止放置6面的时候，加速度的理论值为：

对应的测量值矩阵L:

利用最小二乘就能够把12个变量求出来。

随机误差

随机误差主要有两部分，一个是高斯白噪声，一个是bias随机游走。

高斯白噪声

IMU数据连续时间上受到一个均值为0，方差为，各时刻之间相互独立的高斯过程:

其中表示狄拉克函数。

不过需要说明的是，实际上，IMU传感器获取的数据为离散采样，离散和连续高斯白噪声的方差之间存在如下转换关系：

即离散的序列的方差比连续的方差大倍（传感器的采样时间）。

bias随机游走

通常使用维纳过程来建模bias随时间连续变化的过程，离散时间下称之为随机游走。

bias的变化的导数是其中是方差为1的白噪声。

同样，离散和连续之间的转换为：

bias随机游走的噪声方差离散的序列比连续的大倍（传感器的采样时间）。

随机误差的标定（艾伦方差标定）

Allan方差法是20世纪60年代由美国国家标准局的David Allan提出的，它是一种基于时域的分析方法。具体流程如下：

1. 保持传感器绝对静止获取数据

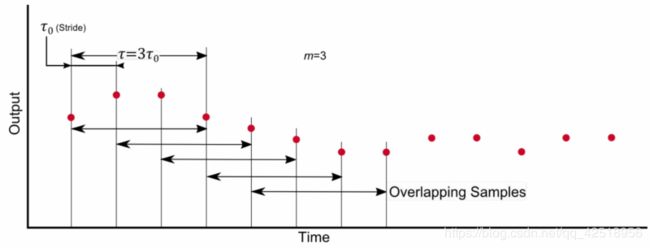
2. 对数据进行分段，设置时间段的时长，如下图所示。

3. 将传感器数据按照时间段进行平均。

4. 计算方差，绘制艾伦曲线。

• 此处的艾伦方差的计算公式如下（将每个时间段长度作为一个变量，将每个时间段的数据求均值，计算方差）：

• 忽略其他噪声的影响，Allan方差可以近似为各种噪声的和，化简为：

其中，Q:量化噪声误差系数；N：角速度随机游走误差系数；B：零偏不稳定性误差系数；K：速率随机游走误差系数；R：速率斜坡误差系数

(ps:其中表格中B那一项是乘法不是除法，写错了)

这里，绘制出来的艾伦曲线如下图所示：

其中t=1，斜率为-0.5处纵坐标的值为高斯白噪声方差，斜率为0.5，t=3处的纵坐标的值为随机游走方差。

下面给出两个github上的比较好用的标定工具。

1. imu_utils，额注意，这个工具的结果关于bias那一项输出的是bias稳定性的方差，不是随机游走的方差，因此，我们需要此工具生成的艾伦方差曲线自行完成bias随机游走方差的获得。。

2. kalibr_allan

加上误差模型后的理论测量值

• 加速度计

• 陀螺仪

• 低端传感器，可能会出现加速度影响陀螺仪的值的情况，也就是下面的第二项：