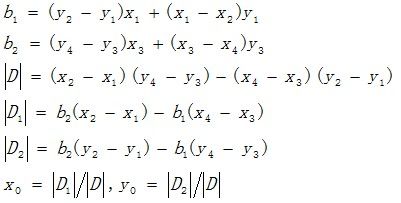计算几何-求线段交点算法和代码（C++语言）

原文地址：计算几何-求线段交点算法和代码（C++语言）

问题描述：已知两条线段P1P2和Q1Q2，判断P1P2和Q1Q2是否相交，若相交，求出交点。

两条线段的位置关系可以分为三类：有重合部分、无重合部分但有交点、无交点。

 

算法核心

算法的步骤如下：

1.快速排斥实验。

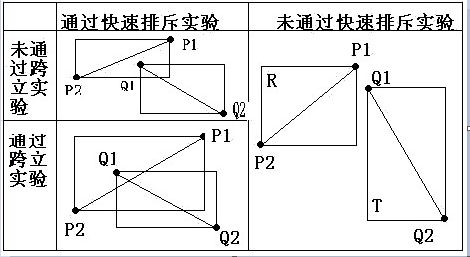
设以线段P1P2为对角线的矩形为R，设以线段Q1Q2为对角线的矩形为T，如果R和T不相交，则两线段不相交。

所以P1P2和Q1Q2相交的必要条件是以他们为对角线的矩形相交，即：

min(p1.x,p2.x) <= max(q1.x,q2.x) &&
min(q1.x,q2.x) <= max(p1.x,p2.x) &&
min(p1.y,p2.y) <= max(q1.y,q2.y) &&
min(q1.y,q2.y) <= max(p1.y,p2.y);

2.跨立实验。

如果两线段相交，则两线段必然相互跨立对方。
线段的跨立究竟是什么意思？向量的跨立是什么意思？

a、若P1P2跨立Q1Q2，则矢量(P1-Q1)和(P2-Q1)位于矢量(Q2-Q1)的两侧，即( P1 - Q1 ) × ( Q2 - Q1 ) * ( P2 - Q1 ) × ( Q2 - Q1 ) < 0。

等价于
(Q1.x-P1.x,Q1.y-P1.y) × ( Q1.x-Q2.x,Q1.y-Q2.y ) * ( Q1.x-P2.x,Q1.y-P2.y ) × ( Q1.x-Q2.x,Q1.y-Q2.y ) < 0
等价于
((Q1.x-P1.x)*(Q1.y-Q2.y)-(Q1.y-P1.y)*( Q1.x-Q2.x)) * ((Q1.x-P2.x)*(Q1.y-Q2.y)-(Q1.y-P2.y)*(Q1.x-Q2.x)) < 0

b、若Q1Q2跨立P1P2，则矢量(Q1-P1)和(Q2-P1)位于矢量(P2-P1)的两侧，即( Q1 - P1 ) × ( P2 - P1 ) * ( Q2 - P1 ) × ( P2 - P1 ) < 0。
等价于
(P1.x-Q1.x,P1.y-Q1.y) × ( P1.x-P2.x,P1.y-P2.y ) * ( P1.x-Q2.x,P1.y-Q2.y ) × ( P1.x-P2.x,P1.y-P2.y ) < 0
等价于
((P1.x-Q1.x)*(P1.y-P2.y)-(P1.y-Q1.y)*(P1.x-P2.x)) * ((P1.x-Q2.x)*(P1.y-P2.y)-(P1.y-Q2.y)*( P1.x-P2.x)) < 0

a和b两个不等式同时满足时即可判断两条线段相交。

排斥实验和跨立实验的示例如下图所示。

代码

//跨立判断
bool isLineSegmentCross(const Point &P1,const Point &P2,const Point &Q1,const Point &Q2)
{
    if(
        ((Q1.x-P1.x)*(Q1.y-Q2.y)-(Q1.y-P1.y)*( Q1.x-Q2.x)) * ((Q1.x-P2.x)*(Q1.y-Q2.y)-(Q1.y-P2.y)*(Q1.x-Q2.x)) < 0 &&
        ((P1.x-Q1.x)*(P1.y-P2.y)-(P1.y-Q1.y)*(P1.x-P2.x)) * ((P1.x-Q2.x)*(P1.y-P2.y)-(P1.y-Q2.y)*( P1.x-P2.x)) < 0
    ) 
        return true;
    else
       return false;
}

3.计算交点。

当判定两条线段相交后，可以进行交点的求解，求交点可以用平面几何方法，列点斜式方程来完成。但由于点斜式方程难以处理斜率为0的特殊情况，不方便求解。因而，参用向量法求解交点。

设交点为(x0,y0)，则下列方程组成立：

根据以上方程组，消除参数k1和k2，得到如下方程：

然后求解(x0,y0)，结果如下所示：

 

#include
#define N 10002

/**
算法适用于整形点，不适用于浮点型 
**/

typedef struct Point
{
    int x;
    int y;
}Point;

double min(int x, int y)
{
    return x;
}

double max(int x, int y)
{
    return x>y?x:y;
}

//排斥实验
bool IsRectCross(const Point &p1,const Point &p2,const Point &q1,const Point &q2)
{
    bool ret = min(p1.x,p2.x) <= max(q1.x,q2.x)    &&
                min(q1.x,q2.x) <= max(p1.x,p2.x) &&
                min(p1.y,p2.y) <= max(q1.y,q2.y) &&
                min(q1.y,q2.y) <= max(p1.y,p2.y);
    return ret;
}

/**这段代码不能得到正确答案，故注释
//跨立判断
bool IsLineSegmentCross(const Point &pFirst1,const Point &pFirst2,const Point &pSecond1,const Point &pSecond2)
{
    long line1,line2;
    line1 = pFirst1.x * (pSecond1.y - pFirst2.y) +
        pFirst2.x * (pFirst1.y - pSecond1.y) +
        pSecond1.x * (pFirst2.y - pFirst1.y);
    line2 = pFirst1.x * (pSecond2.y - pFirst2.y) +
        pFirst2.x * (pFirst1.y - pSecond2.y) + 
        pSecond2.x * (pFirst2.y - pFirst1.y);
    if (((line1 ^ line2) >= 0) && !(line1 == 0 && line2 == 0))
        return false;

    line1 = pSecond1.x * (pFirst1.y - pSecond2.y) +
        pSecond2.x * (pSecond1.y - pFirst1.y) +
        pFirst1.x * (pSecond2.y - pSecond1.y);
    line2 = pSecond1.x * (pFirst2.y - pSecond2.y) + 
        pSecond2.x * (pSecond1.y - pFirst2.y) +
        pFirst2.x * (pSecond2.y - pSecond1.y);
    if (((line1 ^ line2) >= 0) && !(line1 == 0 && line2 == 0))
        return false;
    return true;
}
**/

//跨立判断
bool IsLineSegmentCross(const Point &P1,const Point &P2,const Point &Q1,const Point &Q2)
{
    if(
        ((Q1.x-P1.x)*(Q1.y-Q2.y)-(Q1.y-P1.y)*( Q1.x-Q2.x)) * ((Q1.x-P2.x)*(Q1.y-Q2.y)-(Q1.y-P2.y)*(Q1.x-Q2.x)) < 0 ||
        ((P1.x-Q1.x)*(P1.y-P2.y)-(P1.y-Q1.y)*(P1.x-P2.x)) * ((P1.x-Q2.x)*(P1.y-P2.y)-(P1.y-Q2.y)*( P1.x-P2.x)) < 0
    ) 
        return true;
    else
       return false;
}

/**
求线段P1P2与Q1Q2的交点。
先进行快速排斥实验和跨立实验确定有交点再进行计算。
交点（x,y）使用引用返回。
没有验证过
**/
bool GetCrossPoint(const Point &p1,const Point &p2,const Point &q1,const Point &q2,long &x,long &y)
{
    if(IsRectCross(p1,p2,q1,q2))
    {
        if (IsLineSegmentCross(p1,p2,q1,q2))
        {
            //求交点
            long tmpLeft,tmpRight;
            tmpLeft = (q2.x - q1.x) * (p1.y - p2.y) - (p2.x - p1.x) * (q1.y - q2.y);
            tmpRight = (p1.y - q1.y) * (p2.x - p1.x) * (q2.x - q1.x) + q1.x * (q2.y - q1.y) * (p2.x - p1.x) - p1.x * (p2.y - p1.y) * (q2.x - q1.x);

            x = (int)((double)tmpRight/(double)tmpLeft);

            tmpLeft = (p1.x - p2.x) * (q2.y - q1.y) - (p2.y - p1.y) * (q1.x - q2.x);
            tmpRight = p2.y * (p1.x - p2.x) * (q2.y - q1.y) + (q2.x- p2.x) * (q2.y - q1.y) * (p1.y - p2.y) - q2.y * (q1.x - q2.x) * (p2.y - p1.y); 
            y = (int)((double)tmpRight/(double)tmpLeft);
            return true;
        }
    }
    return false;
}

代码2-线段求交模板
http://www.cppblog.com/wicbnu/archive/2009/08/24/94225.html

#include 
#include 
const int N = 100010;
int mark[N];
struct Point
{
    double x,y;
};
struct stline
{
    Point a,b;
} line1,line2, p[N];

int dblcmp(double a,double b)
{
    if (fabs(a-b)<=1E-6) return 0;
    if (a>b) return 1;
    else return -1;
}
//***************点积判点是否在线段上***************
double dot(double x1,double y1,double x2,double y2) //点积
{
    return x1*x2+y1*y2;
}

int point_on_line(Point a,Point b,Point c) //求a点是不是在线段bc上，>0不在，=0与端点重合，<0在。
{
    return dblcmp(dot(b.x-a.x,b.y-a.y,c.x-a.x,c.y-a.y),0);
}
//**************************************************
double cross(double x1,double y1,double x2,double y2)
{
    return x1*y2-x2*y1;
}
double ab_cross_ac(Point a,Point b,Point c) //ab与ac的叉积
{
    return cross(b.x-a.x,b.y-a.y,c.x-a.x,c.y-a.y);
}
int ab_cross_cd (Point a,Point b,Point c,Point d) //求ab是否与cd相交，交点为p。1规范相交，0交点是一线段的端点，-1不相交。
{
    double s1,s2,s3,s4;
    int d1,d2,d3,d4;
    Point p;
    d1=dblcmp(s1=ab_cross_ac(a,b,c),0);
    d2=dblcmp(s2=ab_cross_ac(a,b,d),0);
    d3=dblcmp(s3=ab_cross_ac(c,d,a),0);
    d4=dblcmp(s4=ab_cross_ac(c,d,b),0);

//如果规范相交则求交点
    if ((d1^d2)==-2 && (d3^d4)==-2)
    {
        p.x=(c.x*s2-d.x*s1)/(s2-s1);
        p.y=(c.y*s2-d.y*s1)/(s2-s1);
        return 1;
    }

//如果不规范相交
    if (d1==0 && point_on_line(c,a,b)<=0)
    {
        p=c;
        return 0;
    }
    if (d2==0 && point_on_line(d,a,b)<=0)
    {
        p=d;
        return 0;
    }
    if (d3==0 && point_on_line(a,c,d)<=0)
    {
        p=a;
        return 0;
    }
    if (d4==0 && point_on_line(b,c,d)<=0)
    {
        p=b;
        return 0;
    }
//如果不相交
    return -1;
}

---

线段交点

https://blog.csdn.net/qq_40998706/article/details/87482435

讲解
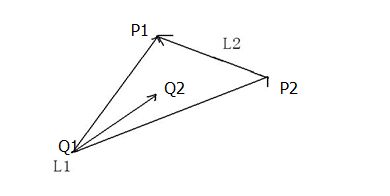
两条线段s1、s2的交点坐标可以通过外积的大小求得。

我们用向量s2.p2 - s2.p1 = base来表示线段s2。接下来，分别求通过s2.p1和s2.p2的直线与线段s1两端点的距离d1、d2。举个例子，设s1.p1 - s2.p1为向量hypo，那么base与hypo构成的平行四边形的面积就是外积base×hypo的大小。这样一来，只要用面积处以base的大小即可求出d1。

d1=∣base×hypo∣/∣base∣ d1=|base×hypo|/|base|d1=∣base×hypo∣/∣base∣
d2 d2d2同理
d1=∣base×(s1.p1−s2.p1)∣/∣base∣ d1=|base×(s1.p1-s2.p1)|/|base|d1=∣base×(s1.p1−s2.p1)∣/∣base∣
d2=∣base×(s1.p2−s2.p1)∣/∣base∣ d2=|base×(s1.p2-s2.p1)|/|base|d2=∣base×(s1.p2−s2.p1)∣/∣base∣
然后，设线段s1的长度与点s1.p1到交点x的距离之比为t，则有
d1:d2=t:(1−t) d1:d2=t:(1-t)d1:d2=t:(1−t)
由此可得
t=d1/(d1+d2) t=d1/(d1+d2)t=d1/(d1+d2)
所以交点x为
x=s1.p1+(s1.p2−s1.p1)×t x=s1.p1+(s1.p2-s1.p1)×tx=s1.p1+(s1.p2−s1.p1)×t
求线段s1与线段s2交点的程序可以像下面这样写

线段s1与线段s2的交点：

Point getCrossPoint(Segment s1, Segment s2) {
    Vector base = s2.p2 - s2.p1;
    double d1 = abs(cross(base, s1.p1 - s2.p1));
    double d2 = abs(cross(base, s1.p2 - s2.p1));
    double t = d1 / (d1 + d2);
    return s1.p1 + (s1.p2 - s1.p1) * t;
}

上述程序在计算d1、d2的过程种会用到|base|，但这个数会在计算t时被约分消去。AC代码如下

#include
#include
#include
using namespace std;

#define EPS (1e-10)
#define equals(a, b) (fabs((a) - (b)) < EPS)

class Point {//Point类，点 
    public:
        double x, y;
        
        Point(double x = 0, double y = 0): x(x), y(y) {}

        Point operator + (Point p) { return Point(x + p.x, y + p.y); }
        Point operator - (Point p) { return Point(x - p.x, y - p.y); }
        Point operator * (double a) { return Point(a * x, a * y); }
        Point operator / (double a) { return Point(x / a, y / a); }

        double abs() { return sqrt(norm()); }
        double norm() { return x * x + y * y; }
        
        bool operator < (const Point &p) const {
            return x != p.x ? x < p.x : y < p.y;
        }

        bool operator == (const Point &p) const {
            return fabs(x - p.x) < EPS && fabs(y - p.y) < EPS;
        }
};

typedef Point Vector;//Vector类，向量 

struct Segment{//Segment 线段 
    Point p1, p2;
};
double dot(Vector a, Vector b) {//内积 
    return a.x * b.x + a.y * b.y;
}

double cross(Vector a, Vector b) {//外积 
    return a.x*b.y - a.y*b.x;
}

Point getCrossPoint(Segment s1, Segment s2) {
    Vector base = s2.p2 - s2.p1;
    double d1 = abs(cross(base, s1.p1 - s2.p1));
    double d2 = abs(cross(base, s1.p2 - s2.p1));
    double t = d1 / (d1 + d2);
    return s1.p1 + (s1.p2 - s1.p1) * t;
}

int main(){
    int q;
    cin>>q;
    
    Segment s1, s2;
    Point p;
    
    while(q--){
        cin>>s1.p1.x>>s1.p1.y>>s1.p2.x>>s1.p2.y>>s2.p1.x>>s2.p1.y>>s2.p2.x>>s2.p2.y;
        p = getCrossPoint(s1, s2);
        printf("%.10f %.10f\n", p.x, p.y);
    }
}