MATLAB——BP神经网络实现
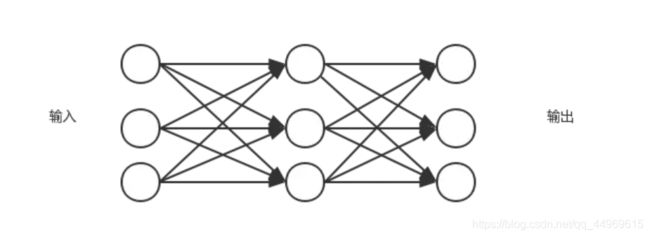
1. 人工神经网络模型拓扑结构
最近呢,高光谱遥感的郭老师又又又给大家布置了两类作业,我自己整理了一下两类作业的思路之后认为,两类作业各有千秋,能够出彩的地方也不尽相同。故我选取大家可能不太熟悉的人工神经网络预测给同学们普及一下。
人工神经网络是由大量简单的基本原件-神经元构成。其主要是通过模拟人的大脑神经处理信息的方式,进行信息并行处理和非线性转换的复杂网络系统。
其优点是多输入多输出实现了数据的并行处理以及自我学习能力,但是神经网络的缺点也是显而易见的,最主要的问题在于处理过程过于“混沌”,可以给出一种比较优秀的结果,但是不能说明为什么是这样的结果。因此神经网络更加适合“经验模型”而非“物理模型”。常用的神经网络由BP网络和RBF网络。BP网络的结构如下:
2. 常用的激励函数
激励函数成为激活函数或者传递函数。常用的形态有三种:
(1)阈值型(一般只用于简单分类的MP模型中):
![]()
(2)线性型(一般用在输入神经元和输出神经元)![]()
(3)S型(常用语隐含层神经元)![]()
通常还会在激励函数的变量中耦合一个常数以便于调整激励网络的输出幅度。
如![]() ,其中c为常量
,其中c为常量
3. 常用神经网络理论
(1)BP网络基本数学原理
常见的BP神经网络拓扑结构。BP网络是一种具有三层或者三层以上神经元的神经网络,包括输入层,中间层(隐含层,且隐含层可以为多层)和输出层。上下层之间完全连接,而同一层之间无连接,输入层神经元语隐含层神经元之减得网络的权值,即两个神经元之间的连接强度。当一对学习样本提供输入神经元后,神经元的激活值(该层神经元的输出值)从输入层经过隐含层想输出层传输,在输出层反向经过各隐含层回到输入层,从而修正各连接权值,这种算法称为“误差反向传播算法”,即BP算法。
BP算法的核心是数学中的“负梯度下降理论”
(2)BP神经网络的结构设计
1准备训练网络的样本
也就是确定输入样本和输出样本
2确定网络的初始参数
包括最大训练次数,隐含层神经元个数,网络学习速率,训练的目标误差,是否添加动量因子等等参数
3初始化网络权值和阈值
训练步骤是按照数据批量形式进行的;数据输入时按照每一行为一个维度进行输入的
4计算第一层神经元的输入和输出
(1) 什么是归一化?
数据归一化,就是将数据映射到[0,1]或[-1,1]区间或更小的区间,比如(0.1,0.9) 。
(2) 为什么要归一化处理?
①输入数据的单位不一样,有些数据的范围可能特别大,导致的结果是神经网络收敛慢、训练时间长。
②数据范围大的输入在模式分类中的作用可能会偏大,而数据范围小的输入作用就可能会偏小。
③由于神经网 络输出层的激活函数的值域是有限制的,因此需要将网络训练的目标数据映射到激活函数的值域。例如神经网络的输出层若采用S形激活函数,由于S形函数的值域 限制在(0,1),也就是说神经网络的输出只能限制在(0,1),所以训练数据的输出就要归一化到[0,1]区间。
④S形激活函数在(0,1)区间以外区域很平缓,区分度太小。例如S形函数f(X)在参数a=1时,f(100)与f(5)只相差0.0067。
(3) 归一化算法
一种简单而快速的归一化算法是线性转换算法。线性转换算法常见有两种形式:
①![]()
其中min为x的最小值,max为x的最大值,输入向量为x,归一化后的输出向量为y 。上式将数据归一化到 [ 0 , 1 ]区间,当激活函数采用S形函数时(值域为(0,1))时这条式子适用。
②![]()
这条公式将数据归一化到 [ -1 , 1 ] 区间。当激活函数采用双极S形函数(值域为(-1,1))时这条式子适用。
(4) Matlab数据归一化处理函数
Matlab中归一化处理数据可以采用premnmx , postmnmx , tramnmx 这3个函数。
① premnmx
语法:[pn,minp,maxp,tn,mint,maxt] = premnmx(p,t)
参数:pn: p矩阵按行归一化后的矩阵
minp,maxp:p矩阵每一行的最小值,最大值
tn:t矩阵按行归一化后的矩阵
mint,maxt:t矩阵每一行的最小值,最大值
作用:将矩阵p,t归一化到[-1,1] ,主要用于归一化处理训练数据集。
② tramnmx
语法:[pn] = tramnmx(p,minp,maxp)
参数:minp,maxp:premnmx函数计算的矩阵的最小,最大值
pn:归一化后的矩阵
作用:主要用于归一化处理待分类的输入数据。
③postmnmx
语法: [p,t] = postmnmx(pn,minp,maxp,tn,mint,maxt)
参数:minp,maxp:premnmx函数计算的p矩阵每行的最小值,最大值
mint,maxt:premnmx函数计算的t矩阵每行的最小值,最大值
作用:将矩阵pn,tn映射回归一化处理前的范围。postmnmx函数主要用于将神经网络的输出结果映射回归一化前的数据范围。
5计算第二层神经元的输入和输出
6计算第n层神经元的输入和输出
7计算能量函数E
8计算第n-1层和第n层之间的权值和阈值的调整量
9计算第二层和第一层之间的权值和阈值的调整量
10计算调整之后的权值和阈值
4. 应用实例
(1)保存.mat文件
%% 保存.mat文件
% data=xlsread('土壤样点');
% data1=data(:,3:6);
% data2=data(:,7);
% attributes=data1';
% strength=data2';
% save concrete_data.mat attributes strength;(2)添加数据集
%%
%添加数据集
load concrete_data; %attributes:7;strength:1(3)划分数据集
%% 划分数据集
temp = randperm(size(attributes,2)); %size(A,2)返回的时矩阵A的列数;randperm随机选择
train_num=80;test_num=train_num+1;%设置训练数据以及测试数据起止位置
P_train = attributes(:,temp(1:train_num)); %设置训练数据集和测试数据集
T_train = strength(:,temp(1:train_num));
P_test = attributes(:,temp(test_num:end));
T_test = strength(:,temp(test_num:end));
(4)数据归一化
%% 数据归一化
[p_train,ps_train] = mymapminmax(P_train,0,1); %将矩阵的每一行处理成[0,1]区间
p_test = mapminmax('apply',P_test,ps_train); %根据给定的数据标准化处理映射ps_train,将P_test标准化为Y。
[t_train,ps_output] = mymapminmax(T_train,0,1);(5)构建BP神经网络
%% 开始构建BP网络
net = newff(p_train,t_train,9); %隐含层为9个神经元
%设定参数网络参数
net.trainParam.epochs = 100000; %最大训练次数
net.trainParam.goal = 1e-7; %训练要求精度
net.trainParam.lr = 0.001; %学习速率(6)开始训练
%% 开始训练
net = train(net,p_train,t_train);
(7)测试网络
%% 测试网络
t_sim = sim(net,p_test);
%反归一化
T_sim = mapminmax('reverse',t_sim,ps_output); %根据已有的数据标准化处理结果ps_output,将标准化数据反标准化
R2 = corrcoef(T_sim,T_test);
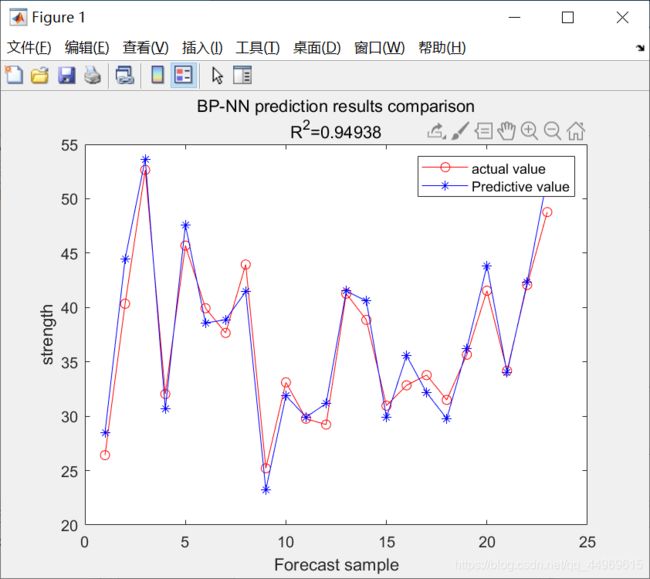
R2 = R2(1,2)^ 2;(8)误差可视化
%% 画出误差图
figure;
plot(1:size(attributes,2)-train_num,T_test,'-or',1:size(attributes,2)-train_num,T_sim,'-*b');
legend('actual value','Predictive value');
xlabel('Forecast sample');
ylabel('strength');
string = {'BP-NN prediction results comparison';['R^2=' num2str(R2)]}; %NN means natural network
title(string);