易懂的对极几何与三维重建概念理解与matlab编程实践
推荐开源项目:简单的SLAM与机器人教程与编程实践-github
破解对极几何中的概念障碍
首先介绍下三维重建到底要做什么事。我们知道一个物体在现实世界的位置是三维的,但是照片是二维的。这意味照片拍摄到的场景丢失了一维。而这一维就是物体离相机的远近。对极几何三维重建就是希望通过多张角度的照片还原各个像素点相对相机的三维坐标。
看本文前你需要了解针孔相机成像原理(即小孔成像原理,参见教程《针孔相机模型成像原理与图像变形矫正教程
》)
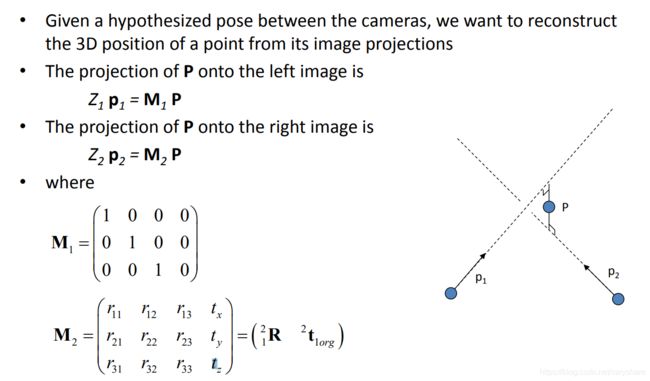
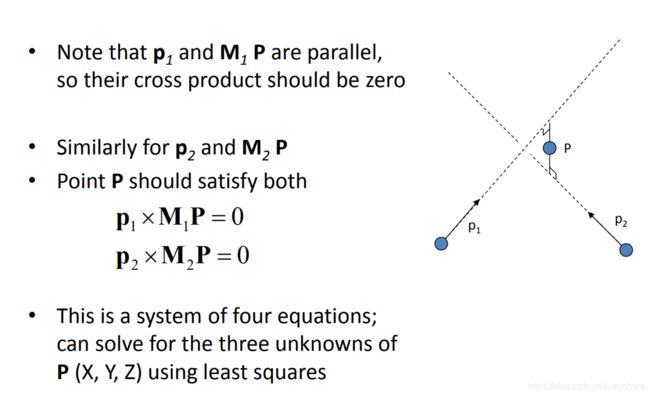
下面这幅图就描述了对极几何。对极几何主要是介绍同一个物体在两个不同的视角下的几何约束关系。而这些几何约束关系对应着一系列等式。通过求解这些等式我们就可以求解得到P相对于第一个视角和第二个视角的坐标。接下来我们看看到底存在哪些几何约束?
注意:
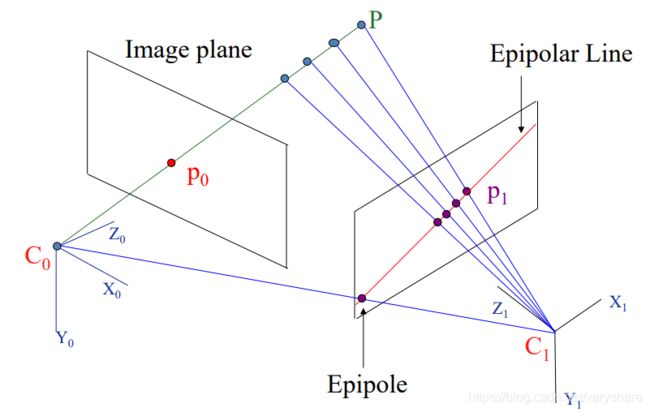
P是现实世界中某一点。 p 0 , p 1 p_0,p_1 p0,p1分别是第0个和第1个视角下物体P被拍摄到的点。注意: p 0 , p 1 p_0,p_1 p0,p1并不是像素点,它们只是损失掉深度值后的点,他们和像素点坐标 x 0 x_0 x0之间的联系是 x 0 = K p 0 x_0=Kp_0 x0=Kp0其中K是相机的内部参数矩阵主要是相机的焦距和原点位置。 C 0 , C 1 C_0,C_1 C0,C1分别是两个不同视角对应的相机焦点。不同视角就是指相机位置姿态发生了变化。
相机成像原理第0个视角下,P点与 p 0 p_0 p0和第一个视角下相机焦点一定在同一条直线上。而且这条直线上的其他现实世界中的点会重合投影到 p 0 p_0 p0。也就是说虽然第0个视角只看到了 p 0 p_0 p0这一个点,但是事实上这个点是由多个点重合投影得到的。那么我怎么知道是否存在重合投影呢?这就是需要第1个视角进行补充约束。大牛们把这约束叫做对极约束。
对极几何进行三维重建的思路
我们从上图中可以看到, P p 0 Pp_0 Pp0这条直线上的点虽然投影到第0个视角是重合到 p 0 p_0 p0但是投影到第1个视角却并不是重合。因此我们根据这些点可以解出红色这条直线(学术上叫做极线Epiolar Line),然后解出极点(Epiplole),然后根据极点和焦点在同一条直线上解出** C 0 C 1 C_0C_1 C0C1这条直线(学术上叫做基线)**。现在我们知道了极线和基线。如果相机位姿没发生变化那么 C 0 C 1 C_0C_1 C0C1这条直线(基线)应该要与极线(Epipolar Line)平行。现在他们不平行了我们只用解出这之间的位姿变化就可以解出两个视角发生的位姿变化。
那么怎么求解红色那条直线(极线Epiolar Line)呢?答:先求出基础矩阵(后面会讲)。根据基础矩阵和像素坐标可以计算出极线的方程。
求解极线(本质矩阵essential matrix)
我们把两条极线,基线独立出来看看他们之间的数学联系。然后根据这些数学联系来计算出极线的数学表达式。
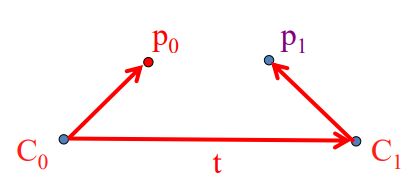
我们知道 C 0 p 0 , C 1 p 1 , C 0 C 1 C_0p_0,C_1p_1,C_0C_1 C0p0,C1p1,C0C1这三个向量是共面的。 C 0 C 1 × C 1 P 1 C_0C_1\times C_1P_1 C0C1×C1P1 注意中间那个乘叫做叉乘(不是内积)。叉乘的结果是一个向量,这个向量与 C 0 C 1 , C 1 P 1 C_0C_1, C_1P_1 C0C1,C1P1均垂直。在高中的立体几何里面我们学过“某直线若垂直一个平面中两条相交直线,那么该直线垂直该平面”。也就是说** C 0 C 1 × C 1 P 1 C_0C_1\times C_1P_1 C0C1×C1P1这个向量与 C 0 p 0 , C 1 p 1 , C 0 C 1 C_0p_0,C_1p_1,C_0C_1 C0p0,C1p1,C0C1所确定的平面垂直,也就是说 C 0 C 1 × C 1 P 1 C_0C_1\times C_1P_1 C0C1×C1P1这个向量与 C 0 p 0 C_0p_0 C0p0也垂直**。我们知道若两个向量垂直那么这两个向量的内积等于0.
于是我们得到了: ( C 0 C 1 × C 1 P 1 ) C 0 p 0 = 0 (C_0C_1\times C_1P_1)C_0p_0=0 (C0C1×C1P1)C0p0=0这个数学表达式。
为了计算方便我们把他们都统一用第0个视角的坐标系表示。当然这意味着我们需要把 C 1 P 1 C_1P_1 C1P1变换到视角0的坐标系下,这个很简单 1 0 R p 1 {}^0_1Rp_1 10Rp1,其中 1 0 R {}^0_1R 10R表示视角1相对视角0发生的旋转,同时 p 1 p_1 p1表示 C 1 P 1 C_1P_1 C1P1在视角1坐标系下的坐标(注意 C 1 C_1 C1就是原点所以可以直接用一个点坐标表示一个向量)。用 t t t表示向量 C 0 C 1 C_0C_1 C0C1
因此有: ( t × 1 0 R p 1 ) p 0 = 0 (t \times {}^0_1Rp_1)p_0=0 (t×10Rp1)p0=0。注意: p 0 , p 1 p_0,p_1 p0,p1都是已知的。为什么?因为他们两个是图片上的特征点,当然很容易知道他们所在的像素位置,进而知道他们在某个视角下的三维坐标。但是 t , 1 0 R t,{}^0_1R t,10R都是未知的需要我们求解。
t × 1 0 R t \times {}^0_1R t×10R这个矩阵很出名学术上叫做本质矩阵。
那么求出本质矩阵有什么用?
注意:R与t之间的联系。矩阵H是视角0变换到视角1的齐次变换矩阵。求出来这个不就知道两个视角发生了怎样的旋转平移变换。

要求解本质矩阵也很容易,我们一对特征点就能得到一个 ( t × 1 0 R p 1 ) p 0 = 0 (t \times {}^0_1Rp_1)p_0=0 (t×10Rp1)p0=0这样的方程。多来几对特征点联立这些方程就能解出本质矩阵了。
跑题了,回答最初的问题“如何求解极线”。我们知道 p 0 ( t × 1 0 R p 1 ) = 0 p_0(t \times {}^0_1Rp_1)=0 p0(t×10Rp1)=0是目前的约束。而一条直线方程可以这么写,我们只需要把 t × 1 0 R p 1 t \times {}^0_1Rp_1 t×10Rp1这部分作为直线的参数即可得到一条直线,这条直线就是极线。
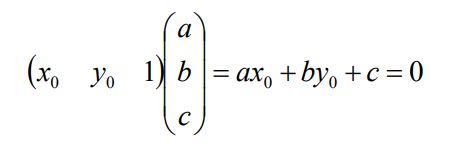
注意:由于 ( t × 1 0 R p 1 ) p 0 = 0 (t \times {}^0_1Rp_1)p_0=0 (t×10Rp1)p0=0这个式子两边不管乘以任何数都是成立的。也就是说我可以任意等比例的放缩本质矩阵的各个元素值。也就是说本质矩阵虽然有9个元素待求,但是由于可以任意放缩,所以我们可以认定有一个值是1,然后就只需要求其他8个元素即可。
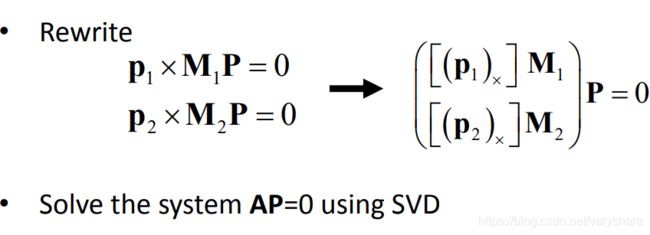
因此我们只需要8个这样的方程就可以求出本质矩阵。也就是说我们只需要8对特征点即可。求解方程的方法是用SVD进行求解。可以参考这篇教程《SVD求解方程原理》。
现在本质矩阵已经可以求解出来。那么怎么根据本质矩阵还原出R和t呢
如何根据R和t还原出点P的在视角1下的三维坐标
基础矩阵与本质矩阵之间的联系?
K p 0 = x 0 Kp_0=x_0 Kp0=x0,其中 x 0 x_0 x0是像素坐标, p 0 = c M P p_0=cMP p0=cMP。
当不知道相机参数K时就得求基础矩阵,因为此时我们只知道像素坐标 x 0 x_0 x0而不知道 p 0 = K − 1 x 0 p_0=K^{-1}x_0 p0=K−1x0。将 x 0 = K − 1 p 0 x_0=K^{-1}p_0 x0=K−1p0代入 p 0 ( t × 1 0 R p 1 ) = 0 p_0(t \times {}^0_1Rp_1)=0 p0(t×10Rp1)=0可得只含有 x 0 x_0 x0的表达式: x 0 K − T t × 1 0 R K − 1 x 1 = 0 x_0 K^{-T} t \times {}^0_1R K^{-1} x_1=0 x0K−Tt×10RK−1x1=0。注意: K − T t × 1 0 R K − 1 K^{-T} t \times {}^0_1R K^{-1} K−Tt×10RK−1这部分叫做基础矩阵,这是要求解的,其他部分就是像素坐标是完全已知的。
你的赞是我愿意持续分享的动力!
参考文献:
[1] https://medium.com/software-incubator/introduction-to-feature-detection-and-matching-65e27179885d
[2] https://medium.com/software-incubator/introduction-to-orb-oriented-fast-and-rotated-brief-4220e8ec40cf
[3] https://www.youtube.com/watch?v=ViNChG-0yX4&list=PL4B3F8D4A5CAD8DA3&index=49
[4] http://inside.mines.edu/~whoff/courses/EENG512/lectures/
[5] http://inside.mines.edu/~whoff/courses/EENG512/lectures/24-EpipolarAndEssential.pdf