GNN的部分理论补充-03
本篇是GNN的部分理论补充
1. 不动点定理
不动点:函数的不动点或定点指的是被这个函数映射到其自身的一个点,即 ξ = f ( ξ ) \xi=f(\xi) ξ=f(ξ)。
压缩映射:设 f f f在区间 [ a , b ] [a,b] [a,b]上定义, f ( [ a , b ] ) ⊂ [ a , b ] f([a, b]) \subset[a, b] f([a,b])⊂[a,b],并存在一个常数 k k k,满足 0 < k < 1 0
压缩映射原理:设 f f f是 [ a , b ] [a,b] [a,b]上的一个压缩映射,则 f f f在 [ a , b ] [a,b] [a,b]中存在唯一的不动点 ξ = f ( ξ ) \xi=f(\xi) ξ=f(ξ),由任何初值 a 0 ∈ [ a , b ] a_{0} \in[a, b] a0∈[a,b]和递推公式 a n + 1 = f ( a n ) , n ∈ N + a_{n+1}=f\left(a_{n}\right), n \in N_{+} an+1=f(an),n∈N+,生成的数列 { a n } \left\{a_{n}\right\} {an}一定收敛于 ξ \xi ξ。
2. 递归求导部分
关于GNN的内容里面提到梯度的求解效率并不高,这里解释说明如下:
假设存在如下递归的式子:
H t + 1 = F ( H t , X ) \mathbf{H}^{t+1}=F\left(\mathbf{H}^{t}, \mathbf{X}\right) Ht+1=F(Ht,X)
函数 F F F的参数使用 W W W表示,现在输入 H 0 \mathbf{H}^0 H0和 X \mathbf{X} X,那么按照时序递归往前计算,有
H 1 = F ( H 0 , X ) H 2 = F ( H 1 , X ) . . . H T = F ( H T − 1 , X ) \begin{aligned} \mathbf{H}^1 &= F(\mathbf{H}^0,\mathbf{X}) \\ \mathbf{H}^2 &= F(\mathbf{H}^1,\mathbf{X}) \\ & ... \\ \mathbf{H}^T &= F(\mathbf{H}^{T-1},\mathbf{X}) \end{aligned} H1H2HT=F(H0,X)=F(H1,X)...=F(HT−1,X)
现在,需要求 H T \mathbf{H}^T HT关于 W W W的偏导数,按照链式法则
∂ H T ( W ) ∂ W = ∂ F ( H T − 1 ( W ) , W ; X ) ∂ W = ∂ F ( H T − 1 , W ; X ) ∂ W + ∂ F ( H T − 1 ( W ) , W ; X ) ∂ H T − 1 ( W ) ⋅ ∂ H T − 1 ( W ) ∂ W \begin{aligned} \frac{\partial{\mathbf{H}^T(W)}}{\partial{W}} &= \frac{\partial{F(\mathbf{H}^{T-1}(W),W;X)}}{\partial{W}} \\ &= \frac{\partial{F(\mathbf{H}^{T-1},W;X)}}{\partial{W}} + \frac{\partial{F(\mathbf{H}^{T-1}(W),W;X)}}{\partial{\mathbf{H}^{T-1}(W)}}\cdot\frac{\partial{\mathbf{H}^{T-1}(W)}}{\partial{W}} \end{aligned} ∂W∂HT(W)=∂W∂F(HT−1(W),W;X)=∂W∂F(HT−1,W;X)+∂HT−1(W)∂F(HT−1(W),W;X)⋅∂W∂HT−1(W)
在此说明一下,公式第一行等号右边将函数写成 F ( H T − 1 ( W ) , W ; X ) F(\mathbf{H}^{T-1}(W),W;X) F(HT−1(W),W;X)的原因是,写在分号 ; ; ;前面的量为与 W W W相关的“函数”,之后需要使用多元微分来求偏微分,分号后面的 X X X由于一直保持不变,所以可以暂时当做常量看待。公式第二行第一项中的 H T − 1 \mathbf{H}^{T-1} HT−1是前向计算的第 T − 1 T-1 T−1时刻的 H \mathbf{H} H的值,不是关于 W W W的函数,第二项中的 W W W是 W W W在 T − 1 T-1 T−1时刻的值,而不是变量。
可以看出,公式最后出现了 ∂ H T − 1 ( W ) ∂ W \frac{\partial{\mathbf{H}^{T-1}(W)}}{\partial{W}} ∂W∂HT−1(W),和公式左边形式差别在于 T − 1 T-1 T−1,因此,按照这样的法则可以一直递归求下去得到最终的 ∂ H T ( W ) ∂ W \frac{\partial{\mathbf{H}^T(W)}}{\partial{W}} ∂W∂HT(W),但是在求的过程中,必须要先按照顺序依次计算出 H 1 . . . H T − 1 \mathbf{H}^1...\mathbf{H}^{T-1} H1...HT−1,然后再逆序地递归求 ∂ H T − 1 ( W ) ∂ W . . . ∂ H 1 ( W ) ∂ W \frac{\partial{\mathbf{H}^{T-1}(W)}}{\partial{W}}...\frac{\partial{\mathbf{H}^1(W)}}{\partial{W}} ∂W∂HT−1(W)...∂W∂H1(W),显然,这个求梯度的过程必须要在完成 T T T次函数 F F F运算之后才能进行,而且还需要递归求解,显然效率比较低。
3. 切比雪夫多项式
ChebNet-2016 核心在于:采用切比雪夫多项式代替谱域的卷积核。
频域上的图卷积存在两个问题:
- 参数矩阵 W W W的参数复杂度与图的节点数线性正相关;
- 频域卷积不具有局部感受野"另外,求特征向量的计算复杂度高,不适用于实时场景下的大图计算。
ChebNet指出可以使用多项式展开近似计算图卷积,即对参数化的频率响应函数进行多项式近似,但是复杂度仍然很高,于是作者使用迭代定义的切比雪夫多项式(ChebShev Polynomial)作近似并证明可以将计算复杂度降低至。![]()
其中K为多项式的阶数,E为图中边的数量。作者将基于切比雪夫多项式定义的卷积核称为切比雪夫卷积核,对应的卷积运算则称为切比雪夫卷积,他们的公式定义如下:

图1. 切比雪夫图卷积的定义
其中 λ max \lambda_{\max } λmax表示拉普拉斯矩阵的最大特征值。从替换和化简后的卷积运算式可以发现,切比雪夫多项式矩阵的运算是固定,可以在预处理阶段完成,且拉普拉斯矩阵一般是稀疏的,可以使用稀疏张量乘法加速,因此整个图卷积的计算复杂度大大降低。除了定义切比雪夫图卷积外,ChebNet的作者还提出了图池化层,此处不展开叙述。
1阶近似与GCN
受ChebNet切比雪夫图卷积的启发,Thomas等人(GCN的作者)提出了一种更加简单的图卷积变种GCN。GCN相当于对一阶切比雪夫图卷积的再近似。在切比雪夫卷积核定义的基础上,我们令多项式的阶数K=1,再令矩阵L的大特征值为2(带来的缩放效应可以通过网络学习自动适应),则图卷积运算过程可以按如下过程进一步简化:

GCN的卷积核更小,参数量也更少,计算复杂度也随之减小,它等价于最简的一阶切比雪夫卷积。上图中倒数第三行的变换被称为“重归一化技巧”,GCN的作者指出,前者的特征值范围是在区间[0,2]内的,所以在神经网络当中多次反复运用这样的算子(多层堆叠)会导致梯度消失和梯度爆炸的问题,为此他们使用归一化技巧将其转化成后者。而我们从吴晓明老师团队的图滤波半监督学习的研究中了解到,重归一化技巧能够将特征值范围进一步缩小以使滤波器变得更加低通,这也是一种有力的解释。
对比ChebNet和GCN,ChebNet的复杂度和参数量比GCN要高,但是表达能力强。ChebNet的K阶卷积算子可以覆盖节点的K阶邻居节点,而GCN则只覆盖一阶邻居节点,但是通过堆叠多个GCN层也可以扩大图卷积的感受域,所以灵活性比较高。最重要的是复杂度较低的GCN相比之前的方法都更加易于训练,速度快且效果好,实用性很强,所以成为了倍最多提到的典型方法(当前引用量为1094)。
总的来看,频谱图卷积网络的研究以图的频谱分析为理论基础,沿着“降低模型复杂度”的主线进行,大多数常规的图运算天然的平方复杂度是掣肘图卷积实用性的主要阻碍,但是最终研究者们还是利用多项式近似和神经网络的适应性一步步将图卷积网络改造到了实用级别,也提高了图卷积网络的研究热度。
4. 图Fourier变换
- 参考知乎
- 参考博客
根据卷积原理,卷积公式可以写成
f ∗ g = F − 1 { F { f } ⋅ F { g } } f * g=\mathcal{F}^{-1}\{\mathcal{F}\{f\} \cdot \mathcal{F}\{g\}\} f∗g=F−1{F{f}⋅F{g}}
正、逆Fourier变换
F ( v ) = ∫ R f ( x ) e − 2 π i x ⋅ v d x \mathcal{F}(v)=\int_{\mathrm{R}} f(x) e^{-2 \pi i x \cdot v} d x F(v)=∫Rf(x)e−2πix⋅vdx
f ( x ) = ∫ R F ( v ) e 2 π i x ⋅ v d v f(x)=\int_{\mathbb{R}} \mathcal{F}(v) e^{2 \pi i x \cdot v} d v f(x)=∫RF(v)e2πix⋅vdv
一阶导数定义
f ′ ( x ) = lim h → 0 f ( x + h ) − f ( x ) h f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} f′(x)=h→0limhf(x+h)−f(x)
拉普拉斯相当于二阶导数
Δ f ( x ) = lim h → 0 f ( x + h ) − 2 f ( x ) + f ( x − h ) h 2 \Delta f(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-2 f(x)+f(x-h)}{h^{2}} Δf(x)=h→0limh2f(x+h)−2f(x)+f(x−h)
在graph上,定义一阶导数为
f ∗ g ′ ( x ) = f ( x ) − f ( y ) f_{* g}^{\prime}(x)=f(x)-f(y) f∗g′(x)=f(x)−f(y)
对应的拉普拉斯算子定义为
Δ ∗ g f ′ ( x ) = Σ y ∼ x ( f ( x ) − f ( y ) ) \Delta_{*g} f^{\prime}(x)=\Sigma_{y \sim x} (f(x)-f(y)) Δ∗gf′(x)=Σy∼x(f(x)−f(y))
假设 D D D为 N × N N\times{N} N×N的度矩阵(degree matrix)
D ( i , j ) = { d i if i = j 0 otherwise D(i, j)=\left\{\begin{array}{ll}{d_{i}} & {\text { if } i=j} \\ {0} & {\text { otherwise }}\end{array}\right. D(i,j)={di0 if i=j otherwise
A A A为 N × N N\times{N} N×N的邻接矩阵(adjacency matrix)
A ( i , j ) = { 1 if x i ∼ x j 0 otherwise A(i, j)=\left\{\begin{array}{ll}{1} & {\text { if } x_{i} \sim x_{j}} \\ {0} & {\text { otherwise }}\end{array}\right. A(i,j)={10 if xi∼xj otherwise
那么图上的Laplacian算子可以写成
L = D − A L=D-A L=D−A
标准化后得到
L = I N − D − 1 2 A D − 1 2 L=I_{N}-D^{-\frac{1}{2}} A D^{-\frac{1}{2}} L=IN−D−21AD−21
定义Laplacian算子的目的是为了找到Fourier变换的基。
传统Fourier变换的基就是Laplacian算子的一组特征向量
Δ e 2 π i x ⋅ v = λ e 2 π i x ⋅ v \Delta e^{2 \pi i x \cdot v}=\lambda e^{2 \pi i x \cdot v} Δe2πix⋅v=λe2πix⋅v
类似的,在graph上,有
Δ f = ( D − A ) f = L f \Delta{f}=(D-A)f=Lf Δf=(D−A)f=Lf
图拉普拉斯算子作用在由图节点信息构成的向量 f f f上得到的结果等于图拉普拉斯矩阵和向量 f f f的点积。
那么graph上的Fourier基就是 L L L矩阵的 n n n个特征向量 U = [ u 1 … u n ] U=\left[u_{1} \dots u_{n}\right] U=[u1…un], L L L可以分解成 L = U Λ U T L=U \Lambda U^{T} L=UΛUT,其中, Λ \Lambda Λ是特征值组成的对角矩阵。
传统的Fourier变换与graph的Fourier变换区别

将 f ( i ) f(i) f(i)看成是第 i i i个点上的signal,用向量 x = ( f ( 1 ) … f ( n ) ) ∈ R n x=(f(1) \ldots f(n)) \in \mathbb{R}^{n} x=(f(1)…f(n))∈Rn来表示。矩阵形式的graph的Fourier变换为
G F { x } = U T x \mathcal{G F}\{x\}=U^{T} x GF{x}=UTx
类似的graph上的Fourier逆变换为
I G F { x } = U x \mathcal{I} \mathcal{G} \mathcal{F}\{x\}=U x IGF{x}=Ux
5. RNN系列模型
推荐阅读
RNN的处理对象:RNN通常处理的是序列输入(sequence),比如一个句子,或者一段视频。
句子中的前后相邻的词汇是相互联系的,而且是有序的,在理解一段句子时,需要按照顺序排列整个序列,与此类似,视频中每一帧之间也是相互联系且是有序,理解一段视频需要有序的播放。
RNN相关任务
-
文本分类:输入一段句子,模型预测该句子所属的类别
比如有三类文本,类别为 { 军事类 , 医疗类 , 科技类 } \{\text{军事类},\text{医疗类},\text{科技类}\} {军事类,医疗类,科技类},模型输入一段句子,并将该句子归类到这三类中的一类,比如
某某公司新出了一种治疗感染的特效药属于医疗类。 -
词性预测:输入一段句子,模型预测该句子每个词汇的词性
比如输入一句话
我吃苹果,那么模型的输出为我(nn) 吃(v) 苹果(nn)。
RNN和普通前馈神经网络比较:以上述任务为例,如果使用普通神经网络,可以将输入的句子作为特征向量直接进行分类,但是,这样做忽略了句子中词汇之间的关联性,比如在吃这个动词后,很有可能接着是一个名词,而不太可能是一个动词,这种有序关系的建模使用普通的网络较难处理。
基础RNN模型
基础的RNN模型示意图如下

蓝色框RNN表示一个RNNcell,在这个cell里面进行向量运算的操作, X X X表示输入的向量值, Y Y Y表示输出的向量值,自连接的弧线表示cell输出的值会作为下一时刻的输入。将上图中RNN的cell操作按照时时序进行展开(按照序列输入的先后),得到如下图

其中的 a a a就是RNN的cell的自连接弧的输出或输入。
如果将RNN的cell按照时序进行展开,得到如下图
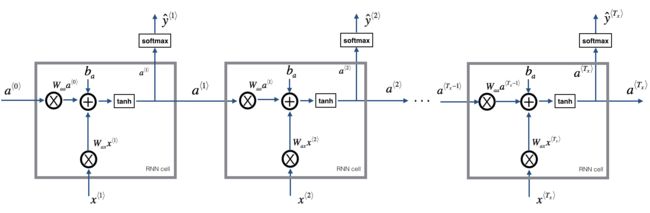
可以看出,在每一个时刻,输入为该时刻的输入 x < t > x^{

根据上图可以看出,第一层的输出 G G G作为第二层的输入,网络的输出为第二层的输出 V V V。
RNN缺点:原始的RNN在训练过程中可能会产生梯度爆炸或消失(可以参见),因此,需要对训练过程采取一些措施,比如梯度裁剪,将梯度强制限制在饱和梯度范围内。此外还有双层双向RNN,多层循环RNN等扩展模型。
长短期记忆(LSTM)
动手学深度学习
LSTM参考
根据前面RNN的模型可以看出,RNN的关键点之一是可以将先前的信息使用到后面的时刻,对于短句子,比比如the cloud in the [sky],预测的关键词sky和前文的距离较短,RNN可以学会使用先前的信息,但是,对于长句子,比如I grew up in France...I speak fluent [French].,如果我们需要模型预测出应该是哪一种语言,由于French和前文的距离很长,那么模型需要考虑位置很远的相关信息。然而,对于较长的句子,RNN会丧失连接如此远信息的能力。
LSTM(Long Short Term Memory)网络,是一种RNN的变体,可以学习到长期的依赖信息,LSTM通过刻意的设计来避免长期依赖问题,使得LSTM结构本身就具有记住长期信息的能力。LSTM的结构示意图如下


LSTM关键在于cell的状态,这个状态类似于传送带,在图上方的水平线上贯穿运行,如下图

LSTM通过精心设计的gate(门)的结构来实现去除或者增加信息到细胞状态,门就是一种让信息选择式通过的方法,包含一个sigmoid层和一个按位的乘法操作,sigmoid层输出0到1之间的值,描述每个部分有多少量可以通过。门机制结构如下示意图
- Forget gate 遗忘门,使用 f f f表示;
- Input gate 输入门 ,使用 i i i表示;
- Output gate 输出门,使用 o o o表示。
第1步:决定我们会从细胞状态中丢弃或保留哪些信息
这个门输入 h t − 1 \mathbf{h_{t-1}} ht−1和 x t \mathbf{x_t} xt,输出一个在0到1之间的数值(向量),然后与上一时刻的细胞状态 C t − 1 \mathbf{C}_{t-1} Ct−1的按元素相乘。如下:

第2步:确定什么样的新信息被存放在细胞状态中
包含两个部分,一个部分是sigmoid层为输入门,决定需要输入多少信息,另一部分是tanh层,用于创建该时刻的输入信息向量 C ~ t \mathbf{\widetilde{C}}_t C t,这个向量用于之后加入到细胞状态中。示意图如下
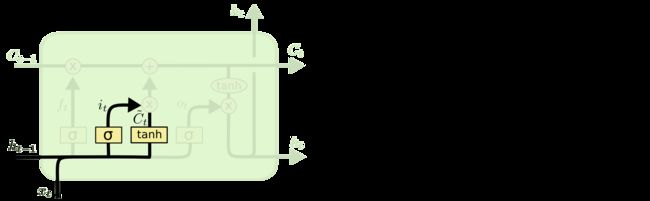
第3步:需要更新旧的细胞状态 C t − 1 \mathbf{C}_{t-1} Ct−1
首先将旧状态与 f t f_t ft相乘,表示需要过滤哪些信息,然后和这一时刻输入的信息相加,表示将该时刻的信息加入到细胞状态,示意图如下
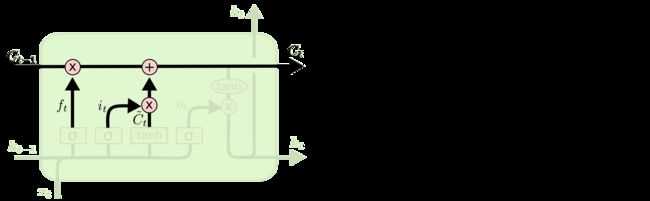
第4步:基于当前时刻的细胞状态确定输出什么值
这也是一个过滤后的信息,首先通过一个tanh层进行处理,得到输出信息的形式,然后通过一个sigmoid层来确定输出哪些信息。
由此,可以得到最后的输出 h t \mathbf{h_t} ht,如下示意图
通过不断进行以上过程,就可以将一个序列(比如句子)编码成最终的输出向量,然后通过这个输出向量经过全连接层进行分类或回归,另外,类似于RNN,通过叠加两个LSTM的cell来得到两层的LSTM,以得到更高级的句子representation。
6个公式汇集如下:
i t = σ ( W ( i ) x t + U ( i ) h t − 1 + b ( i ) ) f t = σ ( W ( f ) x t + U ( f ) h t − 1 + b ( f ) ) o t = σ ( W ( o ) x t + U ( o ) h t − 1 + b ( o ) ) u t = tanh ( W ( u ) x t + U ( u ) h t − 1 + b ( o ) ) c t = i t ⊙ u t + f t ⊙ c t − 1 h t = o t ⊙ tanh ( c t ) \begin{aligned} i_{t} &=\sigma\left(W^{(i)} x_{t}+U^{(i)} h_{t-1}+b^{(i)}\right) \\ f_{t} &=\sigma\left(W^{(f)} x_{t}+U^{(f)} h_{t-1}+b^{(f)}\right) \\ o_{t} &=\sigma\left(W^{(o)} x_{t}+U^{(o)} h_{t-1}+b^{(o)}\right) \\ u_{t} &=\tanh \left(W^{(u)} x_{t}+U^{(u)} h_{t-1}+b^{(o)}\right) \\ c_{t} &=i_{t} \odot u_{t}+f_{t} \odot c_{t-1} \\ h_{t} &=o_{t} \odot \tanh \left(c_{t}\right) \end{aligned} itftotutctht=σ(W(i)xt+U(i)ht−1+b(i))=σ(W(f)xt+U(f)ht−1+b(f))=σ(W(o)xt+U(o)ht−1+b(o))=tanh(W(u)xt+U(u)ht−1+b(o))=it⊙ut+ft⊙ct−1=ot⊙tanh(ct)
门控循环单元(GRU)
引入了重置门(reset gate)和更新门(update gate)的概念,从而修改了循环神经网络中隐藏状态的计算方式。相比于LSTM,GRU将忘记门和输入门合成了一个单一的更新门。同样还混合了细胞状态和隐藏状态,加诸其他一些改动。最终的模型比标准的 LSTM 模型要简单,也是非常流行的变体。
网络详细说明和实现细节参考动手学深度学习。
应用
RNN适合应用于序列型输入,每个时刻的输入的token需要是一个向量,通过取每一时刻的输出或者最后一个时刻的输出来得到句子的representation,用于文本相关的下游任务,比如文本分类、词性标注、机器翻译等等。
其中较为关键的是如何将序列的每一个token转化为向量输入,一般情况下有如下几种方法:
-
随机初始化:在模型初始化阶段给每一个token随机初始化赋予一个向量,然后在loss优化过程中使用随机梯度下降法进行学习。
-
使用统计表征:最简单的就是one-hot向量,假设所有token的总数为 N N N,一个token对应的向量为
E t = [ 0 , 0 , . . . 1 , . . . , 0 ] , E t ∈ R N E_t=[0,0,...1,...,0],E_t\in{R^N} Et=[0,0,...1,...,0],Et∈RN -
使用预训练词向量:通过word2vec对训练预料进行预训练得到预训练词向量,相当于将每一个token转化成一个vector,使用这个vector作为RNN模型每一时刻的输入向量即可。

