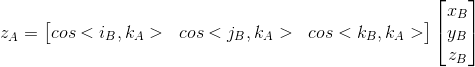- Octo:伯克利开源机器人开发框架
【摘要】在各种机器人数据集上预先训练的大型策略有可能改变机器人学习:这种通用机器人策略无需从头开始训练新策略,只需使用少量领域内数据即可进行微调,但具有广泛的泛化能力。然而,为了广泛应用于各种机器人学习场景、环境和任务,这些策略需要处理不同的传感器和动作空间,适应各种常用的机器人平台,并轻松高效地微调到新领域。在这项工作中,我们旨在为开发开源、广泛适用的通用机器人操作策略奠定基础。作为第一步,我们
- matlab 欧拉角转四元数
点云侠
matlab与合成孔径雷达matlab开发语言算法
目录一、概述一、概述1、计算原理2、实现步骤3、主要函数三、代码实现四、结果展示一、概述目录一、概述一、概述1、计算原理2、实现步骤3、主要函数三、代码实现四、结果展示一、概述 将欧拉角转换为四元数是计算机图形学、机器人学和物理仿真中常见的任务。欧拉角通过一系列的角度描述物体在空间中的旋转,而四元数则提供了一种更加简洁和稳定的方式来实现旋转表示。设欧拉角为(α,β,γ)(\alpha,\beta
- 第九章:LeRobot自定义硬件集成指南
贾全
实战具身智能机器人算法机器人学习人工智能机器学习
引言在前面的章节中,我们学习了如何使用LeRobot进行模仿学习、仿真实验以及摄像头配置。然而,真正的机器人研究往往需要使用自定义的硬件平台。每个研究团队或开发者可能都有自己独特的机器人设计,如何将这些自定义硬件无缝集成到LeRobot生态系统中,是实现高效机器人学习的关键。本章将详细介绍LeRobot的硬件集成框架,帮助读者掌握如何将自己的机器人硬件接入LeRobot系统。通过学习本章内容,你将
- 第八章:LeRobot摄像头配置与应用指南
贾全
实战具身智能机器人深度学习人工智能算法机器学习机器人
引言在机器人学习系统中,视觉感知是至关重要的组成部分。摄像头作为机器人的"眼睛",为系统提供环境信息,使机器人能够理解周围世界并做出相应的决策。LeRobot作为一个完整的机器人学习框架,提供了灵活且强大的摄像头支持系统,能够适配多种类型的摄像头设备。本章将详细介绍LeRobot的摄像头配置和使用方法,帮助读者掌握如何在机器人学习项目中有效地集成和使用视觉系统。8.1LeRobot摄像头系统架构L
- ROS的学习链接整理 (基于古月居)
辣椒炒月饼
学习机器人自动驾驶
机器人控制与仿真:http://wiki.ros.org/roscontrol机器人即使定位与地图建模:http://wiki.ros.org/gmappinghttp://wiki.ros.org/hectorslam机械臂相关学习:http://moveit.ros.org/斯坦福大学公开课———机器人学:https://www.bilibili.com/video/av4506104/交通大
- 物理学中的群论:三维空间转动变换
AI天才研究院
AI大模型企业级应用开发实战Agent实战AI人工智能与大数据计算科学神经计算深度学习神经网络大数据人工智能大型语言模型AIAGILLMJavaPython架构设计AgentRPA
物理学中的群论:三维空间转动变换1.背景介绍1.1问题的由来在物理学领域,特别是量子力学和相对论中,研究物体在空间中的运动是至关重要的。物体的位置、速度以及更深层次的内在性质都受到物理定律的严格规范。当讨论物体的旋转运动时,数学描述变得尤为重要。在三维空间中,物体的旋转可以通过一组称为“旋转矩阵”或者“欧拉角”的方式来精确描述。这些描述方式不仅在理论物理学中不可或缺,也是计算机图形学、机器人学、航
- PolyTouch:一种利用触觉扩散策略实现丰富接触操作的稳健多模态触觉传感器
三谷秋水
智能体计算机视觉机器学习机器人计算机视觉人工智能深度学习
25年4月来自MIT和TRI的论文“PolyTouch:ARobustMulti-ModalTactileSensorforContact-richManipulationUsingTactile-DiffusionPolicies”。在非结构化的家庭环境中实现稳健的灵巧操作仍然是机器人技术的重大挑战。即使采用最先进的机器人学习方法,触觉无关控制策略(即仅依赖外部视觉和/或本体感觉的策略)也常常由
- 矩阵运算与求导全面教程
矩阵运算与求导全面教程矩阵运算与矩阵求导是机器学习、强化学习、数值计算、量子计算、机器人学等领域的核心数学工具。本教程从基础概念出发,逐步深入高级主题,结合理论推导、编程实现、跨领域应用和数值优化技巧,旨在帮助读者全面掌握矩阵相关知识,并灵活应用于实际问题。第一部分:矩阵运算基础1.1矩阵的定义与基本概念矩阵是一个按行和列排列的数字阵列,通常表示为:A=[a11a12⋯a1na21a22⋯a2n⋮
- 【SLAM】基于拓展卡尔曼滤波实现激光雷达传感器和角点提取的机器人定位附matlab代码
matlab科研社
机器人matlab数据结构
✅作者简介:热爱科研的Matlab仿真开发者,擅长数据处理、建模仿真、程序设计、完整代码获取、论文复现及科研仿真。往期回顾关注个人主页:Matlab科研工作室个人信条:格物致知,完整Matlab代码及仿真咨询内容私信。内容介绍自主移动机器人定位是机器人学研究的核心问题之一。本文探讨了基于拓展卡尔曼滤波(EKF)融合激光雷达传感器数据和角点提取技术实现机器人定位的方法。通过深入分析激光雷达传感器的工
- 具身智能 - 推动通用机器人智能的新里程碑:AgiBot World 平台与 GO-1 模型深度解析
天机️灵韵
VLA具身智能人工智能机器人深度学习人工智能具身智能
机器人操作是人工智能与物理世界交互的核心能力,但长期以来受限于高质量数据的稀缺。近期,上海人工智能实验室与AgiBotInc.联合发布了AgiBotWorldColosseo——一个开源的大规模机器人操作平台,包含数据集、工具链与通用策略模型,旨在推动机器人智能向更通用、更灵活的方向发展。本文将从背景、数据集设计、模型架构与实验结果四部分,解析这一平台的创新与突破。一、背景:机器人学习的核心挑战传
- 提炼总结—机器人学导论(原书第四版)(第12章)
kobeban
机器人
写在最前面的话为什么做该博客?该博客的特点是什么?随着DeepSeek、ChatGPT等AI技术的崛起,促使机器人技术发展到了新的高度,诞生了宇树科技、特斯拉为代表的人形机器人,四足机器人等等,越来越多的科技巨头涌入机器人赛道,行业对于相关人才的需求也随之达到了顶峰。本博客的内容是替你阅读所有关于机器人的经典书籍,采用书籍瘦身计划,帮你提炼出核心内容,采用最通俗易懂的语言来解释原理,将书读薄。大大
- 路径规划算法概论:从理论到实践
weixin_47233946
算法
##引言路径规划(PathPlanning)是机器人学、自动驾驶、物流优化、游戏开发等领域的核心技术,旨在为移动主体(如机器人、车辆)找到从起点到目标点的最优或可行路径。随着人工智能和计算能力的提升,路径规划算法在动态环境处理、多目标优化和实时响应方面持续演进。本文将系统梳理路径规划算法的核心分类、基本原理及应用案例。---##一、路径规划算法的核心分类###1.1传统图搜索算法**核心思想**:
- 以人类演示视频为提示,学习可泛化的机器人策略
三谷秋水
大模型智能体计算机视觉机器人计算机视觉深度学习语言模型人工智能
25年5月来自清华大学、上海姚期智研究院和星动纪元(RoboEra)公司的论文“LearningGeneralizableRobotPolicywithHumanDemonstrationVideoasaPrompt”。最近的机器人学习方法通常依赖于从通过遥操作收集的大量机器人数据集中进行模仿学习。当面对新任务时,此类方法通常需要收集一组新的遥操作数据并微调策略。此外,遥操作数据收集流程也很繁琐且
- AI人工智能与机器人学习的未来展望
AI原生应用开发
ai
AI人工智能与机器人学习的未来展望关键词:AI人工智能、机器人学习、具身智能、多模态交互、人机协作、伦理挑战、自主决策摘要:本文将带您走进AI与机器人学习的奇妙世界,从“家庭机器人小助手”的故事出发,用通俗易懂的语言解释多模态交互、具身智能等核心概念,结合算法原理、实战案例和前沿趋势,探讨未来AI机器人如何像人类一样学习、思考与协作,同时揭示技术背后的伦理挑战与发展方向。读完本文,您不仅能理解AI
- 使用 SymPy 操作三维向量的反对称矩阵
老歌老听老掉牙
矩阵线性代数sympy
在三维空间中,一个3×13\times13×1向量可以转换为一个3×33\times33×3的反对称矩阵。这种转换在物理学、机器人学和计算机视觉等领域非常有用。本文将详细介绍如何在Python的SymPy库中定义和使用这种反对称矩阵。数学背景对于一个三维向量v=[v1v2v3]\mathbf{v}=\begin{bmatrix}v_1\\v_2\\v_3\end{bmatrix}v=v1v2v3,
- 仿真环境中机器人抓取与操作上手指南
LIUDAN'S WORLD
人形机器人系统:理论与实践机器人人工智能pytorch
仿真环境中机器人抓取与操作上手指南针对“仿真环境中机器人抓取与操作”项目的上手指南,旨在帮助具备基本机器人学知识的开发者快速实现一个简单的“拿起并放置”(PickandPlace)任务。指南包含可运行的代码示例、安装步骤和简要的理论背景,适用于UbuntuLTS(20.04或22.04)及对应的ROS版本(Noetic或Humble)。关键要点目标:实现一个简单的PickandPlace任务,整合
- 【学习笔记】Sophus (Python) 使用文档
chase。
笔记python
以下是一份针对Sophus库的Python使用文档,涵盖基础概念、安装方法、核心功能及代码示例。内容围绕SO3(3D旋转群)和SE3(3D刚体变换群)展开,适合机器人学、SLAM、三维几何等领域。Sophus(Python)使用文档目录Sophus简介安装方法核心对象与操作SO3:3D旋转群SE3:3D刚体变换群常用功能与示例创建旋转/变换对象转换不同表示形式位姿插值(Slerp/Lerp)李代数
- IsaacLab从入门到精通(二) 导入自定义机器人
NathanWu7
IsaacLab机器人人工智能深度学习机器学习
IsaacLab从入门到精通(二)导入自定义机器人1.1URDF与USD简介现在有很多资料介绍这些文件格式,作者在这里就简单进行一下介绍,URDF(UnifiedRobotDescriptionFormat)文件是一种基于XML的文件格式,用于描述机器人的模型,包括其物理和视觉属性,重点在关节(Joint)和连杆(Link),没有基础的同学可以先学习一下《机器人学》,利用ROS简单测试一下各个机器
- 人工智能、深度学习、机器学习的联系与区别
AI方案2025
人工智能深度学习机器学习
定义人工智能(AI-ArtificialIntelligence):是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。它旨在让计算机能够像人类一样思考、学习和决策,涉及到诸如计算机视觉、自然语言处理、机器人学等多个领域。例如,智能机器人可以感知周围环境(通过传感器)、进行简单的推理(根据预设规则或算法)并做出行动(如移动、抓取物体等)。机器学习(ML-Mach
- (原创)机器人学:从空间变换到正逆向运动学
Shujia_Lee
机器人学
从空间变换到正逆向运动学(一)前言空间变换的数学描述1.空间变换的基本概念2.旋转矩阵的性质3.几种常见的姿态描述方法4.小结前言一直有计划开个坑,写一个比较系统完整的博客专栏,一方面是有利于自己巩固所学的知识,对学习历程做一个记录;另一方面,也希望其他有志于机器人领域的像博主一样的萌新,能够在入门的时候获得一些帮助,得到一些比较系统的知识。这个专栏初定普通机器人学(其实是想到《普通心理学》这个书
- 论文翻译:OK-Robot: What Really Matters in Integrating Open-Knowledge Models for Robotics
YYGe
机器人深度学习人工智能机器人预训练模型
OK-Robot:WhatReallyMattersinIntegratingOpen-KnowledgeModelsforRoboticsOK-Robot:整合开放知识模型在机器人学中的真正重要性文章目录OK-Robot:WhatReallyMattersinIntegratingOpen-KnowledgeModelsforRoboticsOK-Robot:整合开放知识模型在机器人学中的真正重
- 机器人学习算法解析与自主学习系统研究
纸上沉思bJ
机器人学习算法
```html机器人学习算法解析与自主学习系统研究机器人学习算法解析与自主学习系统研究随着人工智能技术的飞速发展,机器人学习算法成为了研究热点之一。机器人学习不仅涉及传统的控制理论和机器学习方法,还结合了强化学习、深度学习等现代技术手段,为实现更加智能、灵活的机器人提供了可能。本文将对机器人学习算法进行详细解析,并探讨其在构建自主学习系统中的应用。一、机器人学习的基本概念机器人学习是指通过某种方式
- 机器人学习入门必看:AI人工智能基础理论与实践
AI天才研究院
计算AI大模型应用入门实战与进阶机器人学习人工智能ai
机器人学习入门必看:AI人工智能基础理论与实践关键词:机器人学习、AI基础理论、机器学习、深度学习、强化学习、机器人控制、实践案例摘要:本文面向机器人学习入门者,系统梳理AI人工智能核心理论体系,深度解析机器学习、深度学习、强化学习等关键技术与机器人控制的融合逻辑。通过数学模型推导、Python算法实现、完整项目实战,构建从理论到实践的知识闭环。涵盖工业机器人、服务机器人等典型应用场景,提供系统化
- MuJoCo Playground 机器人强化学习入门教程(一)
强化学习与机器人控制仿真
MuJoCo仿真与控制教程机器人人工智能深度学习开发语言自动驾驶stm32python
系列文章目录目录系列文章目录前言一、学习RL智能体1.1使用braxPPO进行培训1.2使用RSL-RL进行训练二、欢迎来到MuJoCoPlayground!2.1介绍2.2滚动2.3RL2.4PPO2.5实现可视化推出2.6DM控制套件-体验一下!2.7环境可视化2.8训练2.9PPO2.10SAC前言我们介绍的MuJoCoPlayground是一个完全开源的机器人学习框架,由MJX构建,其明确
- RT-2论文深度解读:视觉-语言-动作统一模型的机器人泛化革命
zhaoyqcsdn
VLA机器学习自然语言处理人工智能经验分享笔记
1.核心问题与挑战传统机器人学习存在两大瓶颈:数据效率低下:依赖特定场景的机器人操作数据(如抓取、推压),收集成本高泛化能力局限:模型仅能完成训练中出现过的任务,无法应对长尾场景RT-2的创新目标:利用互联网规模的视觉语言预训练知识,实现机器人技能的零样本(zero-shot)迁移2.方法论突破2.1统一语义空间构建数据范式革新:将机器人动作表示为"语言化"Token序列(如move_to(x=0
- Pybotics:机器人学的Python工具箱
凤瑶熠Paulette
Pybotics:机器人学的Python工具箱pyboticsThePythonToolboxforRobotics项目地址:https://gitcode.com/gh_mirrors/py/pyboticsPybotics是一个开源的Python工具箱,专注于机器人运动学和校准。该项目主要使用Python语言进行开发。核心功能Pybotics提供了简单、清晰和简洁的接口,可以快速模拟和评估常见
- 【C++游戏引擎开发】《线性代数》(5):四元数的3D旋转原理与实现(含新增Vector3、修改Matrix为非SIMD版本)
JuicyActiveGilbert
C++游戏引擎开发知识点c++游戏引擎线性代数
一、四元数基础理论四元数(Quaternions)是一种扩展了复数系统的数学工具,由威廉·哈密顿(WilliamRowanHamilton)于1843年提出。它在三维空间旋转表示和计算中具有重要应用,尤其在计算机图形学、机器人学和航空航天等领域中因其高效性和无万向节锁的特性而被广泛使用。1.1四元数的定义四元数是一个四维超复数,形式为:q=a+bi+cj+dkq=a+b\mathbf{i}+c\m
- 机器人学习仿真框架
rebekk
具身智能机器人学习
机器人学习仿真框架一般包含(自底向上):3D仿真物理引擎:对现实世界的模拟仿真机器人仿真平台:用于搭建工作场景,以实现agent与环境的交互学习学习算法框架集合:不同的策略学习算法的实现算法测试环境及benchmark:针对不同的定制化算法的测试环境以及评价标准整体框架简要介绍物理引擎:模拟现实世界物理行为的软件工具。可模拟牛顿动力学模型,使用质量、速度、摩擦力和空气阻力等变量,为刚性或柔性物体赋
- TidyBot++:用于机器人学习开源的完整移动机械手
三谷秋水
计算机视觉智能体人工智能机器人开源人工智能机器学习深度学习
24年12月来自普林斯顿、斯坦福和dexterity.ai的论文“TidyBot++:AnOpen-SourceHolonomicMobileManipulatorforRobotLearning”。要充分利用模仿学习在移动机械操作方面的最新进展,需要收集大量人工引导的演示。本文提出一种开源设计,用于设计一种廉价、坚固、灵活的移动机械手,该机械手可支撑任意臂,从而实现各种现实世界的家用移动机械操作
- 机器人基础知识
传说故事
机器人
在机器人学中,“inversedynamics”(逆动力学)和“forwarddynamics”(正向动力学)是两个核心概念,它们帮助我们理解和计算机器人如何移动以及需要应用什么样的力来实现这些移动。InverseDynamics(逆动力学):想象一下你正在试图了解为了让你的机器人的手臂达到某个特定位置或执行某种动作,你需要施加多大的力量。逆动力学就是解决这个问题的方法。它涉及到根据已知的机器人运
- 微信开发者验证接口开发
362217990
微信 开发者 token 验证
微信开发者接口验证。
Token,自己随便定义,与微信填写一致就可以了。
根据微信接入指南描述 http://mp.weixin.qq.com/wiki/17/2d4265491f12608cd170a95559800f2d.html
第一步:填写服务器配置
第二步:验证服务器地址的有效性
第三步:依据接口文档实现业务逻辑
这里主要讲第二步验证服务器有效性。
建一个
- 一个小编程题-类似约瑟夫环问题
BrokenDreams
编程
今天群友出了一题:
一个数列,把第一个元素删除,然后把第二个元素放到数列的最后,依次操作下去,直到把数列中所有的数都删除,要求依次打印出这个过程中删除的数。
&
- linux复习笔记之bash shell (5) 关于减号-的作用
eksliang
linux关于减号“-”的含义linux关于减号“-”的用途linux关于“-”的含义linux关于减号的含义
转载请出自出处:
http://eksliang.iteye.com/blog/2105677
管道命令在bash的连续处理程序中是相当重要的,尤其在使用到前一个命令的studout(标准输出)作为这次的stdin(标准输入)时,就显得太重要了,某些命令需要用到文件名,例如上篇文档的的切割命令(split)、还有
- Unix(3)
18289753290
unix ksh
1)若该变量需要在其他子进程执行,则可用"$变量名称"或${变量}累加内容
什么是子进程?在我目前这个shell情况下,去打开一个新的shell,新的那个shell就是子进程。一般状态下,父进程的自定义变量是无法在子进程内使用的,但通过export将变量变成环境变量后就能够在子进程里面应用了。
2)条件判断: &&代表and ||代表or&nbs
- 关于ListView中性能优化中图片加载问题
酷的飞上天空
ListView
ListView的性能优化网上很多信息,但是涉及到异步加载图片问题就会出现问题。
具体参看上篇文章http://314858770.iteye.com/admin/blogs/1217594
如果每次都重新inflate一个新的View出来肯定会造成性能损失严重,可能会出现listview滚动是很卡的情况,还会出现内存溢出。
现在想出一个方法就是每次都添加一个标识,然后设置图
- 德国总理默多克:给国人的一堂“震撼教育”课
永夜-极光
教育
http://bbs.voc.com.cn/topic-2443617-1-1.html德国总理默多克:给国人的一堂“震撼教育”课
安吉拉—默克尔,一位经历过社会主义的东德人,她利用自己的博客,发表一番来华前的谈话,该说的话,都在上面说了,全世界想看想传播——去看看默克尔总理的博客吧!
德国总理默克尔以她的低调、朴素、谦和、平易近人等品格给国人留下了深刻印象。她以实际行动为中国人上了一堂
- 关于Java继承的一个小问题。。。
随便小屋
java
今天看Java 编程思想的时候遇见一个问题,运行的结果和自己想想的完全不一样。先把代码贴出来!
//CanFight接口
interface Canfight {
void fight();
}
//ActionCharacter类
class ActionCharacter {
public void fight() {
System.out.pr
- 23种基本的设计模式
aijuans
设计模式
Abstract Factory:提供一个创建一系列相关或相互依赖对象的接口,而无需指定它们具体的类。 Adapter:将一个类的接口转换成客户希望的另外一个接口。A d a p t e r模式使得原本由于接口不兼容而不能一起工作的那些类可以一起工作。 Bridge:将抽象部分与它的实现部分分离,使它们都可以独立地变化。 Builder:将一个复杂对象的构建与它的表示分离,使得同
- 《周鸿祎自述:我的互联网方法论》读书笔记
aoyouzi
读书笔记
从用户的角度来看,能解决问题的产品才是好产品,能方便/快速地解决问题的产品,就是一流产品.
商业模式不是赚钱模式
一款产品免费获得海量用户后,它的边际成本趋于0,然后再通过广告或者增值服务的方式赚钱,实际上就是创造了新的价值链.
商业模式的基础是用户,木有用户,任何商业模式都是浮云.商业模式的核心是产品,本质是通过产品为用户创造价值.
商业模式还包括寻找需求
- JavaScript动态改变样式访问技术
百合不是茶
JavaScriptstyle属性ClassName属性
一:style属性
格式:
HTML元素.style.样式属性="值";
创建菜单:在html标签中创建 或者 在head标签中用数组创建
<html>
<head>
<title>style改变样式</title>
</head>
&l
- jQuery的deferred对象详解
bijian1013
jquerydeferred对象
jQuery的开发速度很快,几乎每半年一个大版本,每两个月一个小版本。
每个版本都会引入一些新功能,从jQuery 1.5.0版本开始引入的一个新功能----deferred对象。
&nb
- 淘宝开放平台TOP
Bill_chen
C++c物流C#
淘宝网开放平台首页:http://open.taobao.com/
淘宝开放平台是淘宝TOP团队的产品,TOP即TaoBao Open Platform,
是淘宝合作伙伴开发、发布、交易其服务的平台。
支撑TOP的三条主线为:
1.开放数据和业务流程
* 以API数据形式开放商品、交易、物流等业务;
&
- 【大型网站架构一】大型网站架构概述
bit1129
网站架构
大型互联网特点
面对海量用户、海量数据
大型互联网架构的关键指标
高并发
高性能
高可用
高可扩展性
线性伸缩性
安全性
大型互联网技术要点
前端优化
CDN缓存
反向代理
KV缓存
消息系统
分布式存储
NoSQL数据库
搜索
监控
安全
想到的问题:
1.对于订单系统这种事务型系统,如
- eclipse插件hibernate tools安装
白糖_
Hibernate
eclipse helios(3.6)版
1.启动eclipse 2.选择 Help > Install New Software...> 3.添加如下地址:
http://download.jboss.org/jbosstools/updates/stable/helios/ 4.选择性安装:hibernate tools在All Jboss tool
- Jquery easyui Form表单提交注意事项
bozch
jquery easyui
jquery easyui对表单的提交进行了封装,提交的方式采用的是ajax的方式,在开发的时候应该注意的事项如下:
1、在定义form标签的时候,要将method属性设置成post或者get,特别是进行大字段的文本信息提交的时候,要将method设置成post方式提交,否则页面会抛出跨域访问等异常。所以这个要
- Trie tree(字典树)的Java实现及其应用-统计以某字符串为前缀的单词的数量
bylijinnan
java实现
import java.util.LinkedList;
public class CaseInsensitiveTrie {
/**
字典树的Java实现。实现了插入、查询以及深度优先遍历。
Trie tree's java implementation.(Insert,Search,DFS)
Problem Description
Igna
- html css 鼠标形状样式汇总
chenbowen00
htmlcss
css鼠标手型cursor中hand与pointer
Example:CSS鼠标手型效果 <a href="#" style="cursor:hand">CSS鼠标手型效果</a><br/>
Example:CSS鼠标手型效果 <a href="#" style=&qu
- [IT与投资]IT投资的几个原则
comsci
it
无论是想在电商,软件,硬件还是互联网领域投资,都需要大量资金,虽然各个国家政府在媒体上都给予大家承诺,既要让市场的流动性宽松,又要保持经济的高速增长....但是,事实上,整个市场和社会对于真正的资金投入是非常渴望的,也就是说,表面上看起来,市场很活跃,但是投入的资金并不是很充足的......
- oracle with语句详解
daizj
oraclewithwith as
oracle with语句详解 转
在oracle中,select 查询语句,可以使用with,就是一个子查询,oracle 会把子查询的结果放到临时表中,可以反复使用
例子:注意,这是sql语句,不是pl/sql语句, 可以直接放到jdbc执行的
----------------------------------------------------------------
- hbase的简单操作
deng520159
数据库hbase
近期公司用hbase来存储日志,然后再来分析 ,把hbase开发经常要用的命令找了出来.
用ssh登陆安装hbase那台linux后
用hbase shell进行hbase命令控制台!
表的管理
1)查看有哪些表
hbase(main)> list
2)创建表
# 语法:create <table>, {NAME => <family&g
- C语言scanf继续学习、算术运算符学习和逻辑运算符
dcj3sjt126com
c
/*
2013年3月11日20:37:32
地点:北京潘家园
功能:完成用户格式化输入多个值
目的:学习scanf函数的使用
*/
# include <stdio.h>
int main(void)
{
int i, j, k;
printf("please input three number:\n"); //提示用
- 2015越来越好
dcj3sjt126com
歌曲
越来越好
房子大了电话小了 感觉越来越好
假期多了收入高了 工作越来越好
商品精了价格活了 心情越来越好
天更蓝了水更清了 环境越来越好
活得有奔头人会步步高
想做到你要努力去做到
幸福的笑容天天挂眉梢 越来越好
婆媳和了家庭暖了 生活越来越好
孩子高了懂事多了 学习越来越好
朋友多了心相通了 大家越来越好
道路宽了心气顺了 日子越来越好
活的有精神人就不显
- java.sql.SQLException: Value '0000-00-00' can not be represented as java.sql.Tim
feiteyizu
mysql
数据表中有记录的time字段(属性为timestamp)其值为:“0000-00-00 00:00:00”
程序使用select 语句从中取数据时出现以下异常:
java.sql.SQLException:Value '0000-00-00' can not be represented as java.sql.Date
java.sql.SQLException: Valu
- Ehcache(07)——Ehcache对并发的支持
234390216
并发ehcache锁ReadLockWriteLock
Ehcache对并发的支持
在高并发的情况下,使用Ehcache缓存时,由于并发的读与写,我们读的数据有可能是错误的,我们写的数据也有可能意外的被覆盖。所幸的是Ehcache为我们提供了针对于缓存元素Key的Read(读)、Write(写)锁。当一个线程获取了某一Key的Read锁之后,其它线程获取针对于同
- mysql中blob,text字段的合成索引
jackyrong
mysql
在mysql中,原来有一个叫合成索引的,可以提高blob,text字段的效率性能,
但只能用在精确查询,核心是增加一个列,然后可以用md5进行散列,用散列值查找
则速度快
比如:
create table abc(id varchar(10),context blog,hash_value varchar(40));
insert into abc(1,rep
- 逻辑运算与移位运算
latty
位运算逻辑运算
源码:正数的补码与原码相同例+7 源码:00000111 补码 :00000111 (用8位二进制表示一个数)
负数的补码:
符号位为1,其余位为该数绝对值的原码按位取反;然后整个数加1。 -7 源码: 10000111 ,其绝对值为00000111 取反加一:11111001 为-7补码
已知一个数的补码,求原码的操作分两种情况:
- 利用XSD 验证XML文件
newerdragon
javaxmlxsd
XSD文件 (XML Schema 语言也称作 XML Schema 定义(XML Schema Definition,XSD)。 具体使用方法和定义请参看:
http://www.w3school.com.cn/schema/index.asp
java自jdk1.5以上新增了SchemaFactory类 可以实现对XSD验证的支持,使用起来也很方便。
以下代码可用在J
- 搭建 CentOS 6 服务器(12) - Samba
rensanning
centos
(1)安装
# yum -y install samba
Installed:
samba.i686 0:3.6.9-169.el6_5
# pdbedit -a rensn
new password:123456
retype new password:123456
……
(2)Home文件夹
# mkdir /etc
- Learn Nodejs 01
toknowme
nodejs
(1)下载nodejs
https://nodejs.org/download/ 选择相应的版本进行下载 (2)安装nodejs 安装的方式比较多,请baidu下
我这边下载的是“node-v0.12.7-linux-x64.tar.gz”这个版本 (1)上传服务器 (2)解压 tar -zxvf node-v0.12.
- jquery控制自动刷新的代码举例
xp9802
jquery
1、html内容部分 复制代码代码示例: <div id='log_reload'>
<select name="id_s" size="1">
<option value='2'>-2s-</option>
<option value='3'>-3s-</option
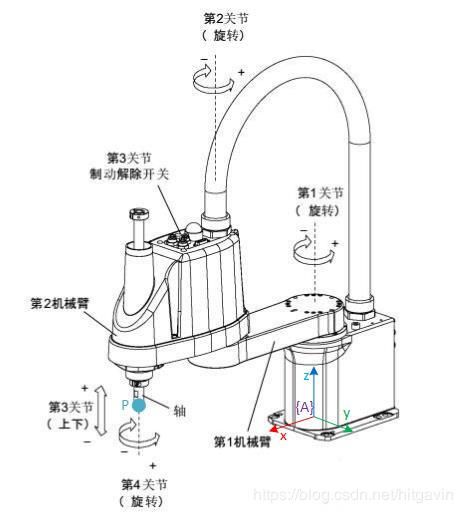
![]() 表示,而在坐标系{B}中可以用向量
表示,而在坐标系{B}中可以用向量![]() 表示。坐标系{B}的原点可以用向量
表示。坐标系{B}的原点可以用向量![]() 表示(注意这些记法的上标代表该向量在哪个坐标系中表达,也就是向量的起点与哪个坐标系的原点重合,下标代表的是空间中的点,比如M代表的是M点。因此
表示(注意这些记法的上标代表该向量在哪个坐标系中表达,也就是向量的起点与哪个坐标系的原点重合,下标代表的是空间中的点,比如M代表的是M点。因此![]() 代表X点在坐标系Y下的向量表示)。根据向量的运算法则,我们很容易得到下面的等价关系
代表X点在坐标系Y下的向量表示)。根据向量的运算法则,我们很容易得到下面的等价关系![]()
![]() 和
和![]() 都代表了点M的坐标,只是参考坐标系不同,一个参考系是坐标系{A},一个参考系是坐标系{B}。那么
都代表了点M的坐标,只是参考坐标系不同,一个参考系是坐标系{A},一个参考系是坐标系{B}。那么![]() 又代表了什么呢?我想你应该能够想到这个代表了两个坐标系之间的位置关系。因此对于只存在平移关系的两个坐标系,我们通过一个三维向量
又代表了什么呢?我想你应该能够想到这个代表了两个坐标系之间的位置关系。因此对于只存在平移关系的两个坐标系,我们通过一个三维向量![]() 就可以描述坐标系{B}与坐标系{A}的关系。上面的等式也就是在只有平移的情况下点在坐标系{A}与{B}之间的坐标变换公式。
就可以描述坐标系{B}与坐标系{A}的关系。上面的等式也就是在只有平移的情况下点在坐标系{A}与{B}之间的坐标变换公式。![]() 。现在我们假设空间中有一点V,那么我们知道这个点既可以在坐标系{A}中表示,又可以在坐标系{B}中表示。设点V在基坐标系{A}下的坐标为:
。现在我们假设空间中有一点V,那么我们知道这个点既可以在坐标系{A}中表示,又可以在坐标系{B}中表示。设点V在基坐标系{A}下的坐标为:![]() ,点V在坐标系{B}中的坐标为
,点V在坐标系{B}中的坐标为![]() ,设O为坐标系{A}和{B}的公共原点。
,设O为坐标系{A}和{B}的公共原点。![]() 其实存在两种分解,第一种是将向量
其实存在两种分解,第一种是将向量![]() 分解到坐标系{A}的三个轴上,此时向量
分解到坐标系{A}的三个轴上,此时向量![]() 可以表示为:
可以表示为:![]() ;第二种是将向量
;第二种是将向量![]() 分解到坐标系{B}的三个轴上,此时向量
分解到坐标系{B}的三个轴上,此时向量![]() 可以表示为:
可以表示为:![]() (注意我们前面已经提到所有的六个坐标轴单位向量都是在基坐标系中描述的)。由于这是同一个向量的两种表示方法。因此我们可以得到如下的等价关系:
(注意我们前面已经提到所有的六个坐标轴单位向量都是在基坐标系中描述的)。由于这是同一个向量的两种表示方法。因此我们可以得到如下的等价关系:![]()
![]() 可以得到:
可以得到:![]()
![]() 可以进一步表示为:
可以进一步表示为:![]() )的两种不同分解(在坐标系{A}中分解得到其在坐标系{A}中的坐标表示,同理在坐标系{B}中分解得到在坐标系{B}中的坐标表示)的等价性已经不自觉地推导出了两个原点重合的坐标系之间的姿态关系,这个关系就是前面提到的矩阵R。
)的两种不同分解(在坐标系{A}中分解得到其在坐标系{A}中的坐标表示,同理在坐标系{B}中分解得到在坐标系{B}中的坐标表示)的等价性已经不自觉地推导出了两个原点重合的坐标系之间的姿态关系,这个关系就是前面提到的矩阵R。