排序算法总结
排序算法总结
概述:
转眼大三了,总结下排序算法,对以后推免,找工作都十分有益。
先来个排序算法总结,再详细讨论。
![]()
一、冒泡排序(Bubble Sort)
第一个就总结学生平时最常用的冒泡排序吧。
1. 基本思想
它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
![]()
2. 详细过程
①. 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
②. 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
③. 针对所有的元素重复以上的步骤,除了最后一个
④. 持续每次对越来越少的元素重复上面的步骤①~③,直到没有任何一对数字需要比较
3. 代码实现
冒泡排序需要两个嵌套的循环. 其中, 外层循环移动游标; 内层循环遍历游标及之后(或之前)的元素, 通过两两交换的方式, 每次只确保该内循环结束位置排序正确, 然后内层循环周期结束, 交由外层循环往后(或前)移动游标, 随即开始下一轮内层循环, 以此类推, 直至循环结束.
public static void bubbleSort(int[] arr){
int temp;
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length-i-1; j++) {
if(arr[j]>arr[j+1]) {
temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
}
算法复杂度等在文章头部。
***提示:***由于冒泡排序只在相邻元素大小不符合要求时才调换他们的位置, 它并不改变相同元素之间的相对顺序, 因此它是稳定的排序算法.
二、快速排序(Quick Sort)
快速排序在面试中经常提到,据说校招能刷下来60%以上的人。
1. 基本思想
快速排序的基本思想:挖坑填数+分治法
首先对无序的记录序列进行“一次划分”,通过一趟排序将待排序列分成两部分,使其中一部分记录的关键字均比另一部分小,再分别对这两部分排序,以达到整个序列有序。
2. 详细步骤
(1)令指针L=1 ,R=n ,即分别指向A1和An;
(2)自尾端开始进行比较:将AR与AL比较,若AL<AR,则数据就不交换,此时固定L(即L指针不动),调整尾指针,使R=R-1。继续比较,直至AL>AR时为止,将AR与AL交换位置,并修改左指针,使L=L+1;
(3)将AL与AR比较,若AL<AR,则调整左指针,使L=L+1,R指针不动。继续比较,直至AL>AR时为止,将AL与AR交换位置,并修改右指针R,使R=R-1;
(4)重复(2)(3)步骤,直到从两边开始的扫描在中间相遇,即L、R指针重合于中间某一个元素,此时该元素即在排序的序列中找到了自己合适的位置,并且此元素将原序列分成了前后两个子集。虽然此时这两个子集还是无序的,但前一个子集的所有元素均小于后一个子集的所有元素。这称为一趟。
3. 代码实现
void quicksort(int r[ ],int left,int right)
{ int i=left, j=right;
int x=r[i];
while (i=x) && (j>i) )
j=j-1; //向前比较
r[i]=r[j]; //比x小的元素左移
while ( (r[i]<=x) && (j>i) )
i=i+1; //向后比较
r[j]=r[i]; } //比x大的元素右移
r[i]=x; //基准值x归位
quicksort(r,left,i-1); //递归调用左子区间
quicksort(r,i+1,right);
三、直接插入排序(Insertion Sort)
1. 基本思想
将数组中的所有元素依次跟前面已经排好的元素相比较,如果选择的元素比已排序的元素小,则交换,直到全部元素都比较过为止。
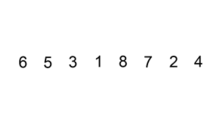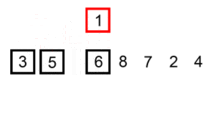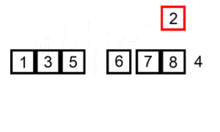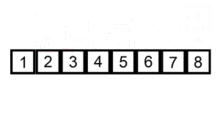
2. 详细过程
①. 从第一个元素开始,该元素可以认为已经被排序
②. 取出下一个元素,在已经排序的元素序列中从后向前扫描
③. 如果该元素(已排序)大于新元素,将该元素移到下一位置
④. 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
⑤. 将新元素插入到该位置后
⑥. 重复步骤②~⑤
![]()
3. 代码实现
public static void insertionSort(int[] arr){
for( int i=0; i0; j-- ) {
if( arr[j-1] <= arr[j] )
break;
int temp = arr[j]; //交换操作
arr[j] = arr[j-1];
arr[j-1] = temp;
System.out.println("Sorting: " + Arrays.toString(arr));
}
}
}
//c语言版本
#include "stdio.h"
#define n 5
int ar[n]; int c,t;
void d_insort(a)
int a[n];
{ int i,j;
for (i=2;i<=n;i++)
{ t=a[i]; j=i-1;
while ((j>0) && (t 提示:由于直接插入排序每次只移动一个元素的位, 并不会改变值相同的元素之间的排序, 因此它是一种稳定排序。
四、希尔排序(Shell Sort)(不如叫希尔插入排序)
1. 基本思想
本质上讲的是插入排序,是对线性插入排序的改进。
先取一个小于n的整数d1并作为第一个增量,将文件的全部记录分成d1个组,所有距离为d1倍数的记录放在同一个组中,在各组内进行直接插入排序;
然后取第二个增量d2
2. 详细步骤
(1)首先选取一个整数d1![]()
3. 代码实现
void shell_sort(a)
int a[max+1];
{ int i,j,n,m,skip; int alldone;
for (i=1;i<=max;i++) index[i]=i; skip=max;
while (skip>1)
{ skip=skip/2;
do { alldone=1;
for (j=1;j<=max-skip;j++)
{ i=j+skip; n=index[i]; m=index[j];
if (a[n]五、选择排序(Selection Sort)
1. 基本思想
选择排序的基本思想:比较 + 交换。
在未排序序列中找到最小(大)元素,存放到未排序序列的起始位置。
2. 详细步骤
①. 从待排序序列中,找到关键字最小的元素;
②. 如果最小元素不是待排序序列的第一个元素,将其和第一个元素互换;
③. 从余下的 N - 1 个元素中,找出关键字最小的元素,重复①、②步,直到排序结束。
![]()
![]()
3. 代码实现
public static void selectionSort(int[] arr){
for(int i = 0; i < arr.length-1; i++){
int min = i;
for(int j = i+1; j < arr.length; j++){ //选出之后待排序中值最小的位置
if(arr[j] < arr[min]){
min = j;
}
}
if(min != i){
int temp = arr[min]; //交换操作
arr[min] = arr[i];
arr[i] = temp;
System.out.println("Sorting: " + Arrays.toString(arr));
}
}
}
//c语言版
void selectsort(elemtype x[],int n)
{ int i,j,small;
elemtype swap;
for(i=0;i六、堆排序(Heap Sort)(堆选择排序)
1. 基本思想
2. 详细步骤
①. 先将初始序列建成一个大顶堆, 那么此时第一个元素最大, 此堆为初始的无序区.
②. 再将关键字最大的记录 (即堆顶, 第一个元素)和无序区的最后一个记录 交换, 由此得到新的无序区和有序区, 且满足
③. 交换 和 后, 堆顶可能违反堆性质, 因此需将调整为堆. 然后重复步骤②, 直到无序区只有一个元素时停止.
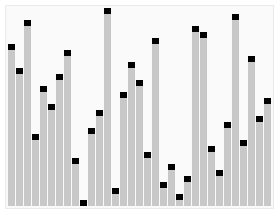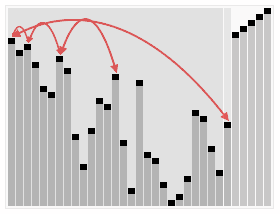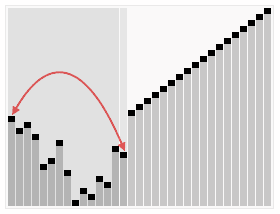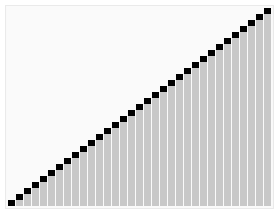
3. 代码实现
从算法描述来看,堆排序需要两个过程,一是建立堆,二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆函数,二是反复调用建堆函数以选择出剩余未排元素中最大的数来实现排序的函数。
总结起来就是定义了以下几种操作:
最大堆调整(Max_Heapify):将堆的末端子节点作调整,使得子节点永远小于父节点
创建最大堆(Build_Max_Heap):将堆所有数据重新排序
堆排序(HeapSort):移除位在第一个数据的根节点,并做最大堆调整的递归运算
对于堆节点的访问:
父节点i的左子节点在位置:(2i+1);
父节点i的右子节点在位置:(2i+2);
子节点i的父节点在位置:floor((i-1)/2);
public static void heapSort(int[] arr){
for(int i = arr.length; i > 0; i--){
max_heapify(arr, i);
int temp = arr[0]; //堆顶元素(第一个元素)与Kn交换
arr[0] = arr[i-1];
arr[i-1] = temp;
}
}
private static void max_heapify(int[] arr, int limit){
if(arr.length <= 0 || arr.length < limit) return;
int parentIdx = limit / 2;
for(; parentIdx >= 0; parentIdx--){
if(parentIdx * 2 >= limit){
continue;
}
int left = parentIdx * 2; //左子节点位置
int right = (left + 1) >= limit ? left : (left + 1); //右子节点位置,如果没有右节点,默认为左节点位置
int maxChildId = arr[left] >= arr[right] ? left : right;
if(arr[maxChildId] > arr[parentIdx]){ //交换父节点与左右子节点中的最大值
int temp = arr[parentIdx];
arr[parentIdx] = arr[maxChildId];
arr[maxChildId] = temp;
}
}
System.out.println("Max_Heapify: " + Arrays.toString(arr));
}
七、归并排序(Merging Sort)
归并排序是建立在归并操作上的一种有效的排序算法,1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递归可以同时进行。
1. 基本思想
归并排序算法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
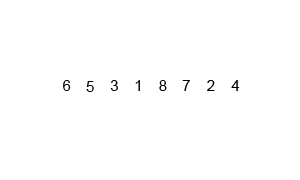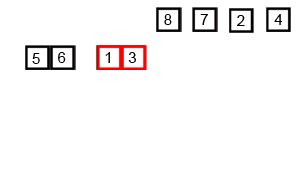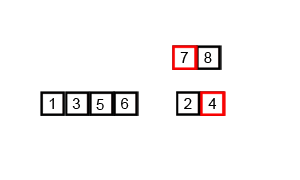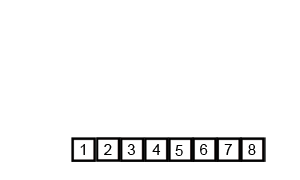
2. 详细步骤
归并排序可通过两种方式实现:
自上而下的递归
自下而上的迭代
一、递归法(假设序列共有n个元素):
①. 将序列每相邻两个数字进行归并操作,形成 floor(n/2)个序列,排序后每个序列包含两个元素;
②. 将上述序列再次归并,形成 floor(n/4)个序列,每个序列包含四个元素;
③. 重复步骤②,直到所有元素排序完毕。
二、迭代法
①. 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
②. 设定两个指针,最初位置分别为两个已经排序序列的起始位置
③. 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
④. 重复步骤③直到某一指针到达序列尾
⑤. 将另一序列剩下的所有元素直接复制到合并序列尾
3. 代码实现
归并排序其实要做两件事:
分解:将序列每次折半拆分
合并:将划分后的序列段两两排序合并
因此,归并排序实际上就是两个操作,拆分+合并
如何合并?
L[first…mid]为第一段,L[mid+1…last]为第二段,并且两端已经有序,现在我们要将两端合成达到L[first…last]并且也有序。
首先依次从第一段与第二段中取出元素比较,将较小的元素赋值给temp[]
重复执行上一步,当某一段赋值结束,则将另一段剩下的元素赋值给temp[]
此时将temp[]中的元素复制给L[],则得到的L[first…last]有序
如何分解?
在这里,我们采用递归的方法,首先将待排序列分成A,B两组;然后重复对A、B序列
分组;直到分组后组内只有一个元素,此时我们认为组内所有元素有序,则分组结束。
这里我写了递归算法如下:
public static int[] mergingSort(int[] arr){
if(arr.length <= 1) return arr;
int num = arr.length >> 1;
int[] leftArr = Arrays.copyOfRange(arr, 0, num);
int[] rightArr = Arrays.copyOfRange(arr, num, arr.length);
System.out.println("split two array: " + Arrays.toString(leftArr) + " And " + Arrays.toString(rightArr));
return mergeTwoArray(mergingSort(leftArr), mergingSort(rightArr)); //不断拆分为最小单元,再排序合并
}
private static int[] mergeTwoArray(int[] arr1, int[] arr2){
int i = 0, j = 0, k = 0;
int[] result = new int[arr1.length + arr2.length]; //申请额外的空间存储合并之后的数组
while(i < arr1.length && j < arr2.length){ //选取两个序列中的较小值放入新数组
if(arr1[i] <= arr2[j]){
result[k++] = arr1[i++];
}else{
result[k++] = arr2[j++];
}
}
while(i < arr1.length){ //序列1中多余的元素移入新数组
result[k++] = arr1[i++];
}
while(j < arr2.length){ //序列2中多余的元素移入新数组
result[k++] = arr2[j++];
}
System.out.println("Merging: " + Arrays.toString(result));
return result;
}
从效率上看,归并排序可算是排序算法中的”佼佼者”. 假设数组长度为n,那么拆分数组共需logn,, 又每步都是一个普通的合并子数组的过程, 时间复杂度为O(n), 故其综合时间复杂度为O(nlogn)。另一方面, 归并排序多次递归过程中拆分的子数组需要保存在内存空间, 其空间复杂度为O(n)。
和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是O(n log n)的时间复杂度。代价是需要额外的内存空间。
八、基数排序(Radix Sort)
基数排序的发明可以追溯到1887年赫尔曼·何乐礼在打孔卡片制表机(Tabulation Machine), 排序器每次只能看到一个列。它是基于元素值的每个位上的字符来排序的。 对于数字而言就是分别基于个位,十位, 百位或千位等等数字来排序。
基数排序(Radix sort)是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。
1. 基本思想
它是这样实现的:将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
基数排序按照优先从高位或低位来排序有两种实现方案:
MSD(Most significant digital) 从最左侧高位开始进行排序。先按k1排序分组, 同一组中记录, 关键码k1相等, 再对各组按k2排序分成子组, 之后, 对后面的关键码继续这样的排序分组, 直到按最次位关键码kd对各子组排序后. 再将各组连接起来, 便得到一个有序序列。MSD方式适用于位数多的序列。
LSD (Least significant digital)从最右侧低位开始进行排序。先从kd开始排序,再对kd-1进行排序,依次重复,直到对k1排序后便得到一个有序序列。LSD方式适用于位数少的序列。
![]() 2. 详细步骤
2. 详细步骤
我们以LSD为例,从最低位开始,具体算法描述如下:
①. 取得数组中的最大数,并取得位数;
②. arr为原始数组,从最低位开始取每个位组成radix数组;
③. 对radix进行计数排序(利用计数排序适用于小范围数的特点);
3. 代码实现
基数排序:通过序列中各个元素的值,对排序的N个元素进行若干趟的“分配”与“收集”来实现排序。
分配:我们将L[i]中的元素取出,首先确定其个位上的数字,根据该数字分配到与之序号相同的桶中
收集:当序列中所有的元素都分配到对应的桶中,再按照顺序依次将桶中的元素收集形成新的一个待排序列L[]。对新形成的序列L[]重复执行分配和收集元素中的十位、百位…直到分配完该序列中的最高位,则排序结束
public static void radixSort(int[] arr){
if(arr.length <= 1) return;
//取得数组中的最大数,并取得位数
int max = 0;
for(int i = 0; i < arr.length; i++){
if(max < arr[i]){
max = arr[i];
}
}
int maxDigit = 1;
while(max / 10 > 0){
maxDigit++;
max = max / 10;
}
System.out.println("maxDigit: " + maxDigit);
//申请一个桶空间
int[][] buckets = new int[10][arr.length];
int base = 10;
//从低位到高位,对每一位遍历,将所有元素分配到桶中
for(int i = 0; i < maxDigit; i++){
int[] bktLen = new int[10]; //存储各个桶中存储元素的数量
//分配:将所有元素分配到桶中
for(int j = 0; j < arr.length; j++){
int whichBucket = (arr[j] % base) / (base / 10);
buckets[whichBucket][bktLen[whichBucket]] = arr[j];
bktLen[whichBucket]++;
}
//收集:将不同桶里数据挨个捞出来,为下一轮高位排序做准备,由于靠近桶底的元素排名靠前,因此从桶底先捞
int k = 0;
for(int b = 0; b < buckets.length; b++){
for(int p = 0; p < bktLen[b]; p++){
arr[k++] = buckets[b][p];
}
}
System.out.println("Sorting: " + Arrays.toString(arr));
base *= 10;
}
}
其中,d 为位数,r 为基数,n 为原数组个数。在基数排序中,因为没有比较操作,所以在复杂上,最好的情况与最坏的情况在时间上是一致的,均为 O(d*(n + r))。
基数排序更适合用于对时间, 字符串等这些整体权值未知的数据进行排序。
Tips: 基数排序不改变相同元素之间的相对顺序,因此它是稳定的排序算法。
基数排序 vs 计数排序 vs 桶排序
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
1.基数排序:根据键值的每位数字来分配桶
2.计数排序:每个桶只存储单一键值
3.桶排序:每个桶存储一定范围的数值
总结
(1). 平方阶O(n²)排序:各类简单排序:直接插入、直接选择和冒泡排序;
(2). 线性对数阶O(nlog₂n)排序:快速排序、堆排序和归并排序;
(3). O(n1+§))排序,§是介于0和1之间的常数:希尔排序
(4). 线性阶O(n)排序:基数排序,此外还有桶、箱排序。
基数排序的时间复杂度是最小的,那么为什么却没有快排、堆排序流行呢?我们看看下图算法导论的相关说明:

基数排序只适用于有基数的情况,而基于比较的排序适用范围就广得多。另一方面是内存上的考虑。作为一种通用的排序方法,最好不要带来意料之外的内存开销,所以各语言的默认实现都没有用基数排序,但是不能否认基数排序在各领域的应用。
说明:
–当原表有序或基本有序时,直接插入排序和冒泡排序将大大减少比较次数和移动记录的次-数,时间复杂度可降至O(n);
–而快速排序则相反,当原表基本有序时,将蜕化为冒泡排序,时间复杂度提高为O(n2);
–原表是否有序,对简单选择排序、堆排序、归并排序和基数排序的时间复杂度影响不大。

最终说明:这个总结很大程度上是仿照u013063153大佬的总结写的,后续我会优化下代码以及相关描述。