Union-Find 算法(并查集)
前言
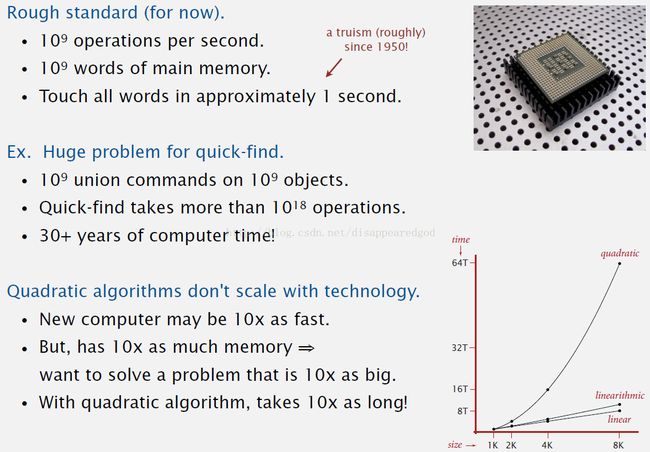
0. 介绍
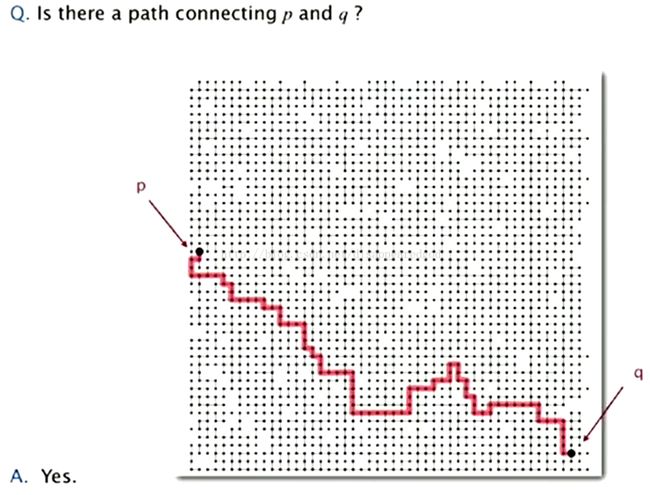
1. 动态连通性
- 自反性:p和p是相连的
- 对称性:如果p和q是相连的,那么q和p也是相连的
- 传递性:如果p和q是相连的且q和r是相连的,那么p和r也是相连的。
void union(int p, int q) add connection between p and q
int find(int p) component identifier for p (0 to N-1)
boolean connected(int p, int q) return true if p and q are in the same component
int count() number of components
所有的实现都应该:
定义一种数据结构表示一直的连接
基于此数据结构实现高效的union()、find()、connected()和count()方法
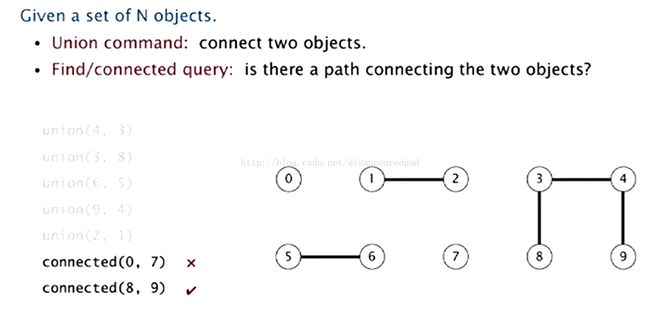
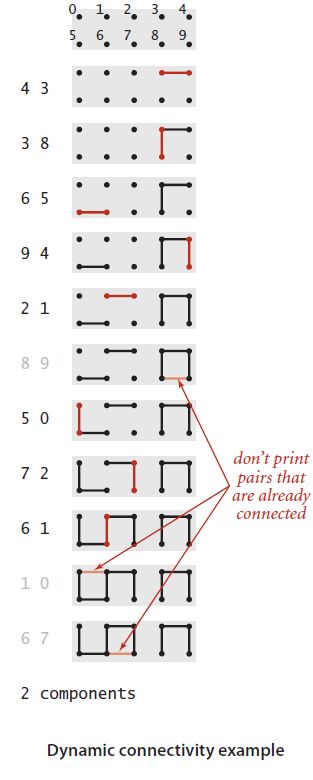
首先,先看一下UF的测试用例
public static void main(String[] args) {
int N = StdIn.readInt();//对象的个数
UF uf = new UF(N);
while (!StdIn.isEmpty()) {//输入整数对
int p = StdIn.readInt();
int q = StdIn.readInt();
if (uf.connected(p, q)) continue;
uf.union(p, q);
StdOut.println(p + " " + q);
}
StdOut.println(uf.count() + " components");
}测试用例的一个输入是:
10
4 3
3 8
6 5
9 4
2 1
8 9
5 0
7 2
6 1
1 0
6 72. 实现
对于上述这样的动态连接问题,我们用下面几种方法进行数显。
2.1 quick-find 算法
2.1.1 算法介绍
我们想构造这样一种数据类型
其实,我们用了一个一下这个方法(例如添加一条边1-6)
我们举几个例子吧:
先从0-链接开始
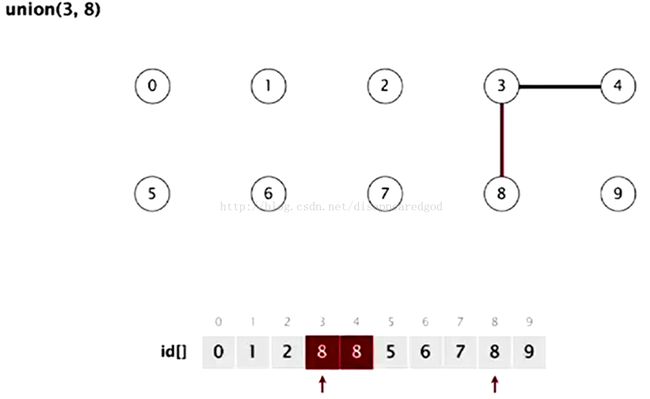
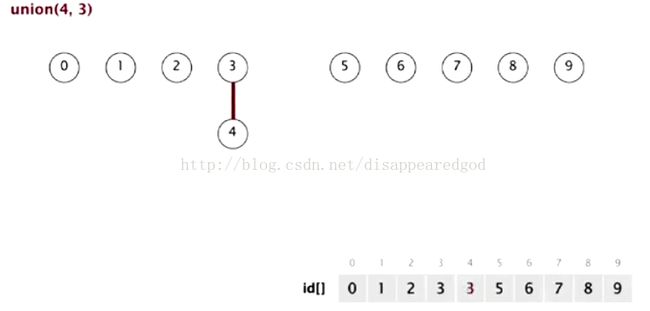
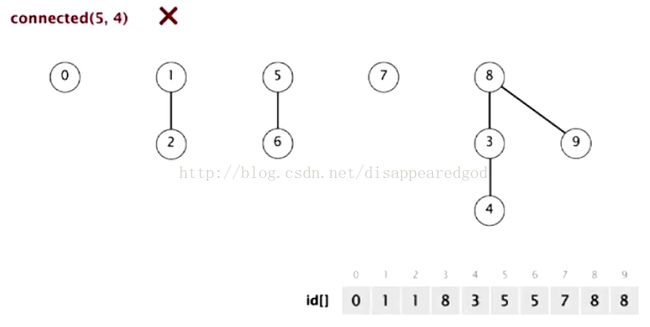
链接操作union(4,3) 就是把id为4的数值改为id为3的数值
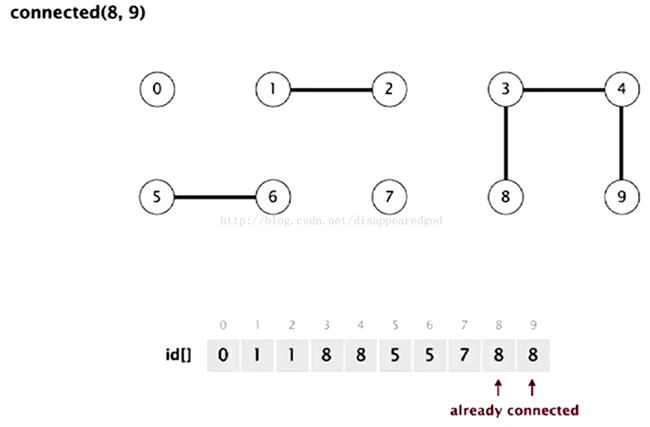
connected()判断是否有链接
如下图来做这个操作
2.1.2 算法实现
根据上述介绍,我们可以写这样段代码
public class QuickFindUF {
private int[] id; // id[i] = component identifier of i
private int count; // number of components
/**
* Initializes an empty union-find data structure with N isolated components 0 through N-1.
* @throws java.lang.IllegalArgumentException if N < 0
* @param N the number of objects
*/
public QuickFindUF(int N) {
count = N;
id = new int[N];
for (int i = 0; i < N; i++)
id[i] = i;
}
/**
* Are the two sites p and q/tt> in the same component?
* @param p the integer representing one site
* @param q the integer representing the other site
* @return true if the two sites p and q are in
* the same component, and false otherwise
* @throws java.lang.IndexOutOfBoundsException unless both 0 <= p < N and 0 <= q < N
*/
public boolean connected(int p, int q) {
return id[p] == id[q];
}
/**
* Merges the component containing sitep with the component
* containing site q.
* @param p the integer representing one site
* @param q the integer representing the other site
* @throws java.lang.IndexOutOfBoundsException unless both 0 <= p < N and 0 <= q < N
*/
public void union(int p, int q) {
if (connected(p, q)) return;
int pid = id[p];
for (int i = 0; i < id.length; i++)
if (id[i] == pid) id[i] = id[q];
count--;
}
/**
* Returns the number of components.
* @return the number of components (between 1 and N)
*/
public int count() {
return count;
}
/**
* Returns the component identifier for the component containing site p.
* @param p the integer representing one site
* @return the component identifier for the component containing site p
* @throws java.lang.IndexOutOfBoundsException unless 0 <= p < N
*/
public int find(int p) {
return id[p];
}
}
2.1.3 算法分析
在quick-find 算法中,每次find()调用只需要访问数组一次,而归并两个分量的union()操作访问数组的次数在(N+3)到(2N+1)之间。(uion中调用两次find(),jiancha id[]数组中全部N个元素并改变他们中的1到N-1个元素)。
如果最终结果是只得到一个连通分量(所有数组值都相同),只扫调用(N-1)次union,即至少需要N+3TimesN-1次——N^2次操作。
2.2 quick-union 算法
2.2.1 介绍
这个算法主要是提高了union()方法的速度,它和quick-find方法互补。
他也是基于相同的数据结构(id数组),单赋予了不同的意义。这里采用了树(根)的概念。
我们由p和q的链接分别找到它们的根触点,然后只需要将一个根触点链接到另一个即可,讲一个分量重命名为另一个分量,因此叫做quick-union。
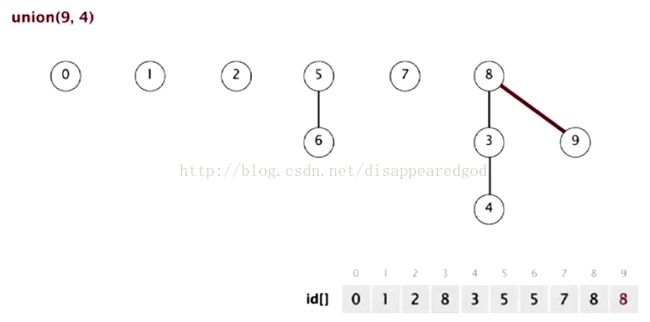
我现在看一下是如何做Union() 和Connect()的
Union(a,b)是将b的根节点作为a的根节点的根节点
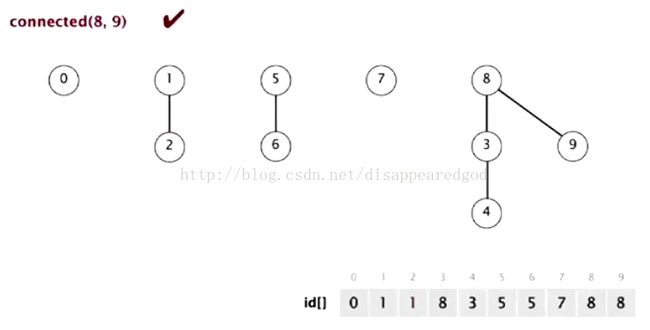
connect(a,b)是看他们的根节点是否相同
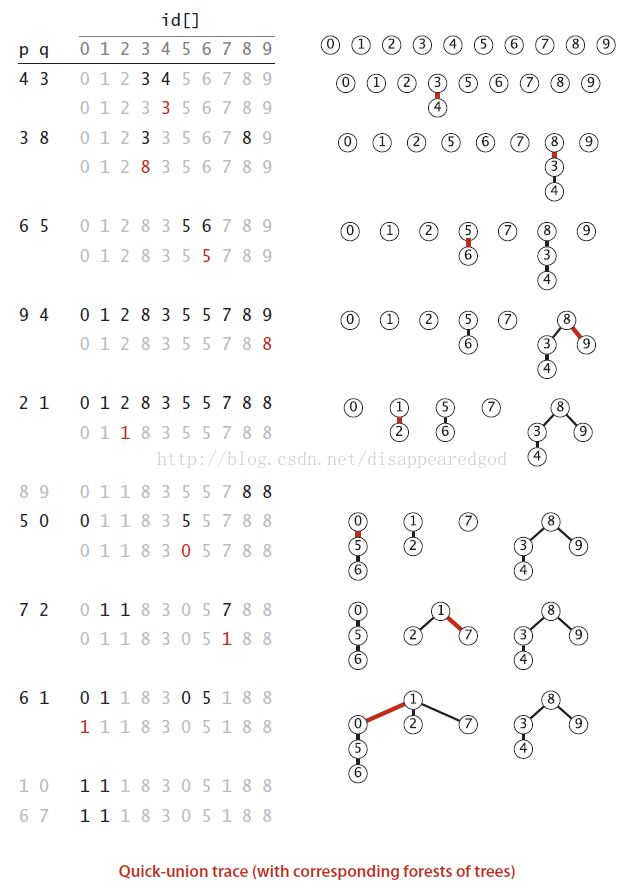
下面看一下这个例子中的树是如何建立的
2.2.2实现
public class QuickUnionUF {
private int[] id; // id[i] = parent of i
private int count; // number of components
/**
* Initializes an empty union-find data structure with N isolated components 0 through N-1.
* @throws java.lang.IllegalArgumentException if N < 0
* @param N the number of objects
*/
public QuickUnionUF(int N) {
id = new int[N];
count = N;
for (int i = 0; i < N; i++) {
id[i] = i;
}
}
/**
* Returns the component identifier for the component containing site p.
* @param p the integer representing one site
* @return the component identifier for the component containing site p
* @throws java.lang.IndexOutOfBoundsException unless 0 <= p < N
*/
public int find(int p) {
while (p != id[p])
p = id[p];
return p;
}
/**
* Are the two sites p and q in the same component?
* @param p the integer representing one site
* @param q the integer representing the other site
* @return true if the sites p and q are in the same
* component, and false otherwise
* @throws java.lang.IndexOutOfBoundsException unless both 0 <= p < N and 0 <= q < N
*/
public boolean connected(int p, int q) {
return find(p) == find(q);
}
/**
* Merges the component containing sitep with the component
* containing site q.
* @param p the integer representing one site
* @param q the integer representing the other site
* @throws java.lang.IndexOutOfBoundsException unless both 0 <= p < N and 0 <= q < N
*/
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
id[rootP] = rootQ;
count--;
}
/**
* Returns the number of components.
* @return the number of components (between 1 and N)
*/
public int count() {
return count;
}
}2.2.3 评价
这个方法的最好的时间复杂度是线性的,最坏时间复杂度也还是平方的。
好处是:quick-union 算法看做是quick-find算法的一种改良,因为它解决了quick-find算法中最主要的问题(Union()操作总是线性级别的)。
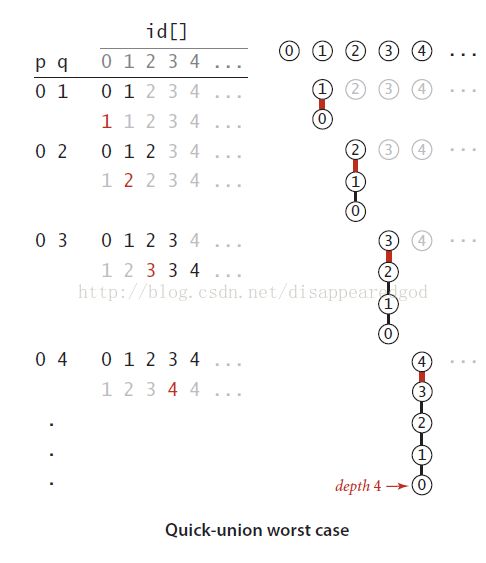
我们发现最坏时间复杂度高是因为树的深度太深。
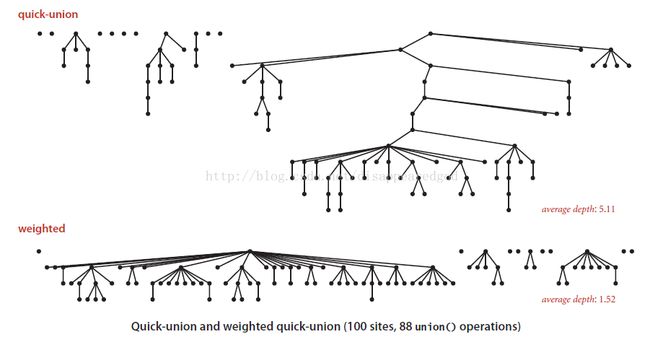
2.3 加权quick-union算法
2.3.1 介绍
简单的修改quick-union算法就能保证最坏情况不能发生。我们将记录每一棵树的大小并总是将较小的树链接到较大的树上。这项改动需要添加一个数组和一些代码在记录树中的节点数。
2.3.2 实现
public class WeightedQuickUnionUF {
private int[] id; // id[i] = parent of i
private int[] sz; // sz[i] = number of objects in subtree rooted at i
private int count; // number of components
/**
* Initializes an empty union-find data structure with N isolated components 0 through N-1.
* @throws java.lang.IllegalArgumentException if N < 0
* @param N the number of objects
*/
public WeightedQuickUnionUF(int N) {
count = N;
id = new int[N];
sz = new int[N];
for (int i = 0; i < N; i++) {
id[i] = i;
sz[i] = 1;
}
}
/**
* Returns the number of components.
* @return the number of components (between 1 and N)
*/
public int count() {
return count;
}
/**
* Returns the component identifier for the component containing site p.
* @param p the integer representing one site
* @return the component identifier for the component containing site p
* @throws java.lang.IndexOutOfBoundsException unless 0 <= p < N
*/
public int find(int p) {
while (p != id[p])
p = id[p];
return p;
}
/**
* Are the two sites p and q in the same component?
* @param p the integer representing one site
* @param q the integer representing the other site
* @return true if the two sites p and q
* are in the same component, and false otherwise
* @throws java.lang.IndexOutOfBoundsException unless both 0 <= p < N and 0 <= q < N
*/
public boolean connected(int p, int q) {
return find(p) == find(q);
}
/**
* Merges the component containing sitep with the component
* containing site q.
* @param p the integer representing one site
* @param q the integer representing the other site
* @throws java.lang.IndexOutOfBoundsException unless both 0 <= p < N and 0 <= q < N
*/
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
// make smaller root point to larger one
if (sz[rootP] < sz[rootQ]) { id[rootP] = rootQ; sz[rootQ] += sz[rootP]; }
else { id[rootQ] = rootP; sz[rootP] += sz[rootQ]; }
count--;
}
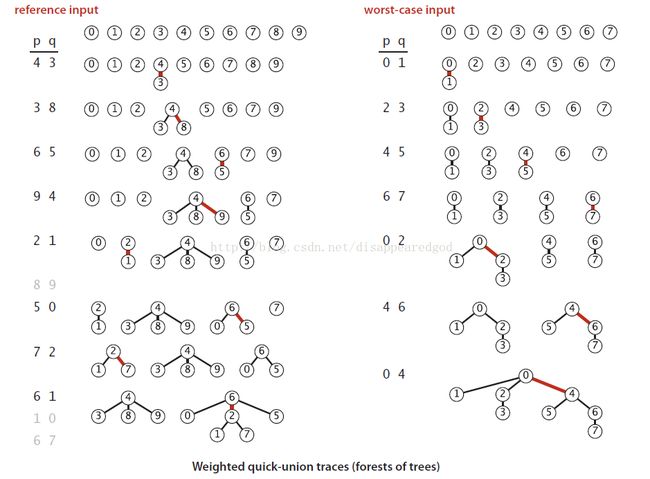
}2.3.3 评价
下图为例子输入构造和上述最坏情况对于100个点做88次union方法来说
2.4 总结
各种UF的性能比较
所有操作的总成本(横轴为链接总数,纵轴为访问数组的次数)