Union-Find问题

1.问题分析

所谓union-find问题就是动态图连通性问题，为什么叫做union-find呢？我认为原因应该是在动态图连通性问题中，union操作是将两个连通子集（connected components）连接起来（不仅仅是连接两个点），find操作是查找是否连通（实际可能会有些不同），是两个十分重要的操作，因此称此类问题为union-find问题。
首先我们认为，连通关系（connected）是一种等价关系，这一点十分重要，这就说明连接关系有以下三个特点：

• 1.自反性（Reflexive）：点p和点p自身是连通关系；
• 2.对称性（Symmetric）：若点p和点q是连通关系，那么点q和点p也是连通关系；
• 3.传递性(Transitive)：若点p和点q是连通关系，点q和点o是连通关系，那么点p和点o也是连通关系。

对于所有点进行分类原则十分简单，就是根据这些点是否属于同一个连通子集中，那么所有点就会分为若干个连通子集。举个例子，假设当图中有十个点，分成了三个连通子集{0,8,9},{1,4,5},{2,3,6,7}那么在只有在同一子集中的点才具有连通关系。显而易见，这些连通子集之间相交均为空集，所有连通子集的并集为全体。注意，根据三个子集可以画出很多种连通图来，但是由于连通关系是一种等价关系，那么其实这些图只是看起来不同，实际上含义是相同的。
其次，在这个问题中，我们需要实现的两个基本操作：

• 1.查询操作(find query)：检查两个点是否属于同一个连通子集；
• 2.连接操作(union command)：将两个连通子集合并成一个子集；
  所以说，这类问题的本质就是对于集合的操作，比如说如何区分不同的子集，如何对子集求并集，找出子集的元素等等。

2.Quick Find方法

2.1方法分析

经过上面的分析，那么我们可以想到，利用整数数组作为数据结构是简单易行的，下面是对此的一些解释：

1.数据结构（data structure）:整形数组（Integer Array），点P和点Q具备连通关系，当且仅当点P和点Q中存储的相同整数。P和Q相当于数组的索引，其中存储的值就是数组的元素。
2.Find操作：检查点P和点Q中的id是否相同；
3.union操作：连接点P和点Q，进行的操作是让点Q所在的连通子集的所有元素的值等于点P所在连通子集的所有元素的值，实现两个集合求并集。注意，若是仅仅让点Q的值等于点P的值，那么仅仅是将点Q从原子集中移到了点P所在的子集，这是不对的，违反了连通关系的传递性(transitive).

2.2 C++代码实现

Sedgewick的《算法，第四版》上有Java代码实现，稍微修改就可以运行，因为我最近在学习C++，因此利用C++写了一遍。
这是定义的“unionfind.h”头文件

#include
using std::vector;

class QuickFindUF{
private:
    vector<int> UF;
public:

    //定义一个默认构造函数
    QuickFindUF() = default;
    //定义一个接收参数构造函数
    QuickFindUF(int N){
        UF = vector<int>(N);
        for (int i = 0; i < N; i++){
            UF[i] = i;
        }
    }
    //定义find成员函数，目的是用来查找索引为i的元素的值
    int find(int p);
    //定义unionFunc成员函数，目的是连接给定的两个点
    void unionFunc(int p, int q);
    //定义connected函数，判断两个点是否连接
    bool connected(int p, int q);
};

int QuickFindUF::find(int p){
    return UF[p];
}
void QuickFindUF::unionFunc(int p, int q){
    /*if (UF[p] != UF[q])
        UF[p] != UF[q];*///这两行代码大错特错，原因就是这里的模型已经是联通集合，那么将两点相连就是将两个集合相连，在这个模型中，必须将两个集合中的标记统一
    if (UF[p] != UF[q]){
        int idp = UF[p];//这两个赋值语句必不可少
        int idq = UF[q];
        for (int i = 0; i != UF.size(); i++){
            if (UF[i] == idq) UF[i] = idp;
        }
    }
}
bool QuickFindUF::connected(int p, int q){
    return UF[p] == UF[q];
}

//这是代码的简单实现
#include 
#include 
#include 
#include "unionfind.h"
using namespace std;
using std::vector;

int main(){
    //新建立一个类的对象，令N = 10；
    QuickFindUF qfObj(10);
    int b = qfObj.find(1);
    bool a = qfObj.connected(1, 2);
    cout << b << endl;
    cout << "connected?" << a << endl;
    qfObj.unionFunc(1, 2);
    bool a1 = qfObj.connected(1, 2);
    cout << "after union,connected?" << a1 << endl;
    qfObj.unionFunc(3, 4);
    bool a2 = qfObj.connected(3, 4);
    cout << "after union,connected?" << a2 << endl;
    bool a3 = qfObj.connected(2, 3);
    cout << "2and3,connected?" << a3 << endl;
    qfObj.unionFunc(1, 4);
    a3 = qfObj.connected(2, 3);
    cout << "after union 1and4,2and3,connected?" << a3 << endl;
    for (int i = 0; i != 10; i++){
        int m = qfObj.find(i);
        cout << "Number " << i << "is" << m << endl;
    }
    return 0;
}

经过上面的测试数据，正确实现了功能。

2.3算法分析

研究算法，对于算法性能分析十分重要，quick-find算法从名字就可以看出来，实现find操作很快，时间复杂度为O(1)，也就是检查两个点是否是连通的。而进行初始化，建立长度为N的数组，时间复杂度为O(N)，这个无法再优化了。union操作的时间复杂度为O(N)，这个很容易看出来，当图中元素很多且union操作需要调用很多时，算法效率就会很低。

3.Quick-Union方法

3.1 方法分析

使用的数据结构仍然是整数数组，下面是对此的解释：

1.数据结构：整形数组，每个点中存储的数据是父节点的索引，根节点存储自身的索引，因此，根节点相同的点就属于同一个连通子集。
2.find操作：检查点P和点Q根节点是否相同。
3.union操作：连接点P和点Q，将点Q的根作为点P的根的根就可以了。

3.1 cpp代码实现

头文件”QuickUnion.h”

#include 
using std::vector;

class QuickUnion{
private:
    vector<int> UF;
public:
    //默认构造函数
    QuickUnion() = default;
    QuickUnion(int N){
        UF = vector<int>(N);//初始化数组,建立不连通图
        for (int i = 0; i != N; i++){
            UF[i] = i;
        }
    }
    //find操作，查找给定节点的root
    int find(int p);
    //union操作，求并集
    void uoionF(int p, int q);
    //connected函数，检查是否连通
    bool connected(int p, int q);
};
int QuickUnion::find(int p){
    while (UF[p] != p){
        p = UF[p];
    }
    return p;
}
void QuickUnion::uoionF(int p, int q){
    //若点P的根和点Q的根不同，就讲点Q的根作为点P的根的根
    int i = find(p);
    int j = find(q);
    UF[i] = j;
}
bool QuickUnion::connected(int p, int q){
    return find(p) == find(q);
}

简单实现和验证，结果正确

#include
#include "QuickUnion.h"
using namespace std;

int main(){
    //新建一个对象，无连接图
    QuickUnion quObj(10);
    int n0 = quObj.find(1);
    cout << "点1的root是 " <1, 2);
    int n1 = quObj.find(1);
    cout << "和点2进行Union操作之后，点1的根是 " << n1 << endl;
    quObj.uoionF(3,4);
    quObj.uoionF(1, 3);
    int n2 = quObj.find(1);
    cout << "和点3进行Union操作之后，点1的根是 " << n2 << endl;
    return 0;
}

3.3 算法分析

初始化的时间复杂度是O(N),这个和之前一样。find操作由于需要寻找节点的root，因此最坏的情况是O（N），union中包含了两步find操作，因此最坏的情况也是O(N)，表面看起来甚至不如QuickFind，但实际使用中，不会出现从底部一直遍历整个数组才找到根部的情况。因此，QuickUnion的union操作的执行效率远比QuickFind的union操作好。

4 带加权的QuickUnion方法

4.1 方法分析

分析QuickUnion方法，若是能让产生的“树形状的子集”（后面简称树）更加扁平化，那么find操作的消耗就会变少，相应的union操作也会变少。思考一个问题：高度为N和高度为M 树合并，如何使新树的高度最小？很简单，让M作为N的子树，M的root直接与N的root相连即满足要求，这就是带加权的QuickUnion(weighted QuickUnion)的做法：

1.数据结构：建立两个整形数组，一个用于存储节点，另一个用于存储每一点的权重。
2.find操作：同QuickUoion，只要两个节点的root相同即可。
3.union操作:首先判断两个子树那个包含的点更多，然后将较小的树作为较大的树的子树子树，改变其root值即可。

4.2 cpp代码实现

头文件”w_quickunion.h”

#include 
using std::vector;

class WQuickUnion{
private:
    vector<int> UF;
    vector<int> SZ;
public:
    //默认构造函数
    WQuickUnion() = default;
    WQuickUnion(int N){
        UF = vector<int>(N);//初始化数组,建立不连通图
        SZ = vector<int>(N);//初始化权值数组，每个元素初始值为1，表明高度为1
        for (int i = 0; i != N; i++){
            UF[i] = i;
            SZ[i] = 1;
        }
    }
    //find操作，查找给定节点的root
    int find(int p);
    //union操作，求并集
    void uoionF(int p, int q);
    //connected函数，QuickUoion
    bool connected(int p, int q);
};
int WQuickUnion::find(int p){
    while (UF[p] != p){
        p = UF[p];
    }
    return p;
}
void WQuickUnion::uoionF(int p, int q){
    //若点P的根和点Q的根不同，就讲点Q的根作为点P的根的根
    int i = find(p);
    int j = find(q);
    if (SZ[i] > SZ[j]){ UF[j] = i; SZ[i] = SZ[j]; }
    else{ UF[i] = j; SZ[j] = SZ[i]; }//这里对权值更新，点少的子树作为新子树
}
bool WQuickUnion::connected(int p, int q){
    return find(p) == find(q);
}

测试文件

#include
#include "w_quickunion.h"
using namespace std;

int main(){
    //新建一个对象，无连接图
    WQuickUnion quObj(10);
    int n0 = quObj.find(1);
    cout << "点1的root是 " << n0 << endl;
    quObj.uoionF(1, 2);
    int n1 = quObj.find(1);
    cout << "和点2进行Union操作之后，点1的根是 " << n1 << endl;
    quObj.uoionF(3, 4);
    quObj.uoionF(1, 3);
    int n2 = quObj.find(1);
    cout << "和点3进行Union操作之后，点1的根是 " << n2 << endl;
    return 0;
}

4.4 算法分析

1. 初始化的时间复杂度仍然为O(N)；
2. find操作的时间复杂度为O（logN）。证明：通俗一点说，有子树T1（内含点x）和子树T2，假设T1的深度小于等于T2，那么应该讲T1作为T2的子树，此时T1深度增加，T2深度不变，那么T1上的任意一个节点的深度都应该加1。此时包含点x的子树的大小（包含点的总数）至少变为原来的2倍，因为| T2 | >= | T1 |，也就是说，包含x点的子树最多只能进行lgN次合并（因为点数为N，每次至少增加2倍），也就是说树的深度最多为lgN；
3. union操作：由于find操作时间复杂度改变，union操作的时间复杂度也相应变为O（lgN）。

5.路径压缩的weighted quickfind算法

5.1 算法分析

基本思路是在进行查找节点的root时，将待查找节点与其root直接相连，那么也就是加一行代码就可以实现了；另一种做法是，将待查找节点所指向root的路径上的每一个节点都变为指向其爷爷节点，那么路径就会缩短一半，也是只需要一行代码就可以实现了。

6 总结

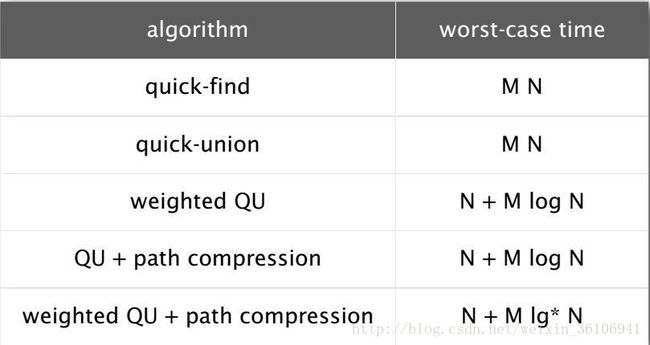
由此表可以看出，经过不断地改进，算法的性能有了很大的提高，然而仅仅需要添加几行代码即可。

WQUPC就是路径压缩的带权值的quickunion算法，耗时由30年变为了6秒，所以好的算法十分重要。设计一个算法时，我们必须考虑算法的性能问题，不断分析和解决，这样才是正确的做法。
我认为UoionFind的问题的本质还是连通子集，中在不同的方法中，连通子集的变化：

1. quick find ：连通子集是简单的集合形式，各个点之间组从集合的无序性。
2. quick union：连通子集是树的形式，各个点之间显然存在一定的顺序和关系。
3. w-quickuoion：连通子集是树的形式，但是相比于quick union，树的深度小很多。
4. WQUPC：连通子集是树的形式，但是理想状态下，该树深度为1。
5. 集合到树再到理想树，理想树就可以看做从普通无序集合中拿出一点作为root，其余不变。也就启发我们应该在某些情况下在数据结构中建立元素之间的联系和有序性，但是这种有序性不能过于复杂。