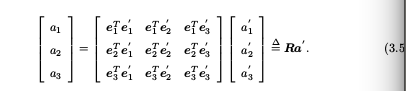《第3讲 三维空间刚体运动 》读书笔记

本文是《视觉SLAM十四讲》第3讲的个人读书笔记，为防止后期记忆遗忘写的。

本节目标

1. 总结旋转矩阵、变换矩阵、四元数和欧拉角各自特点，总结它们之间的相互转换关系。

2.总结 线性代数Eigen 库的矩阵、几何模块的c++使用方法。

 

3.1 旋转矩阵（欧氏变换、旋转矩阵、变换矩阵）

首先我们考虑的对象是刚体,它不光有位置,还有自身的姿态。相机也可以看成三维空间的刚体,于是位置是指相机在空
间中的哪个地方,而姿态则是指相机的朝向。结合起来,我们可以说,“相机正处于空间(0, 0, 0) 点处,朝向正前方” 这样的话。

相机运动是一个刚体运动,它保证了同一个向量在各个坐标系下的长度和夹角都不会发生变化。这种变换称为欧氏变换。

相机视野中某个向量 p,它的坐标为 p c ,而从世界坐标系下看,它的坐标 p w 。这两个坐标之间是如何转换的呢?这时,就需要先得到该点针对机器人坐标系坐标值,再根据机器人位姿转换到世界坐标系中,这个转换关系由一个矩阵 T 来描述,如图所示。

                                                

我们设某个单位正交基(e 1 , e 2 , e 3 ) 经过一次旋转,变成了 (e 1 , e 2 , e 3 )。那么,对于同一个向量 a (注意该向量并没有随着坐标系的旋转而发生运动),它在两个坐标系下的坐标为 [a 1 , a 2 , a 3 ] T 和 [a 1 , a 2 , a 3 ] T 。根据坐标的定义有:

                                                          

                                                                     

矩阵 R 描述了旋转本身。因此它又称为旋转矩阵。旋转矩阵是一个行列式为 1 的正交矩阵 。反之,行列式为 1 的正交矩阵也是一个旋转矩阵。所以,我们可以把旋转矩阵的集合定义如下:。由于旋转矩阵为正交阵,它的逆(即转置)描述了一个相反的旋转。.。

在欧氏变换中,除了旋转之外还有一个平移。考虑世界坐标系中的向量 a,经过一次旋转(用 R 描述)和一次平移 t 后,得到了 a ,那么把旋转和平移合到一起,有:。

上式完整地表达了欧氏空间的旋转与平移,不过还存在一个小问题:这里的变换关系不是一个线性关系。所以引入变换矩阵与齐次坐标。我们把一个三维向量的末尾添加 1,变成了四维向量,称为齐次坐标。

矩阵 T 称为变换矩阵(Transform Matrix)

从而我们可以写成线性的变换公式：。

解该矩阵的逆表示一个反向的变换

---

3.2 实践:Eigen

#include 
#include 
// Eigen 部分
#include 
// 稠密矩阵的代数运算（逆，特征值等）
#include 
#define MATRIX_SIZE 50


using namespace std;
using namespace Eigen;
/****************************
* 本程序演示了 Eigen 基本类型的使用
****************************/

int main( int argc, char** argv )
{

/*************
* 初始化操作
*************/
    // Eigen 中所有向量和矩阵都是Matrix，它是一个模板类。它的前三个参数为：数据类型，行，列
    Matrix f_23;
    Matrix f_31;
    // 同时，Eigen 通过 typedef 提供了许多内置类型，不过底层仍是Matrix
    // 例如 Vector3d 实质上是 Matrix，即三维向量
    Vector3d d_31;
    // Matrix3d 实质上是 Matrix
    Matrix3d d_33 = Matrix3d::Zero(); //初始化为零
    // 如果不确定矩阵大小，可以使用动态大小的矩阵
    Matrix< double, Dynamic, Dynamic > matrix_dynamic;
    // 更简单的
    MatrixXd matrix_x;

/***************
* 矩阵基本操作
***************/
    // 输入数据（初始化）
    f_23 << 1, 2, 3, 4, 5, 6;
    // 输出
    cout << f_23 << endl;
    // 用()访问矩阵中的元素
    for (int i=0; i<2; i++) {
        for (int j=0; j<3; j++)
            cout< result_wrong_type = f_23 * d_31;
    // 应该显式转换
    Matrix result = f_23.cast() * d_31;
    cout << result << endl;
    Matrix result2 = f_23 * f_31;
    cout << result2 << endl;
   
    // 一些矩阵运算(四则运算就不演示了，直接用+-*/即可。)
    d_33 = Matrix3d::Random();      // 随机数矩阵
    cout << d_33 << endl << endl;
    cout << d_33.transpose() << endl;      // 转置
    cout << d_33.sum() << endl;            // 各元素和
    cout << d_33.trace() << endl;          // 迹
    cout << 10*d_33 << endl;               // 数乘
    cout << d_33.inverse() << endl;        // 逆
    cout << d_33.determinant() << endl;    // 行列式

    // 求特征值
    // 实对称矩阵可以保证对角化成功
    SelfAdjointEigenSolver eigen_solver ( d_33.transpose()*d_33 );
    cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;
    cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl;

/**************
* 矩阵解方程操作
**************/
    // 我们求解 matrix_NN * x = v_Nd 这个方程
    // 直接求逆自然是最直接的，但是求逆运算量大
    Matrix< double, MATRIX_SIZE, MATRIX_SIZE > matrix_NN;
    matrix_NN = MatrixXd::Random( MATRIX_SIZE, MATRIX_SIZE );
    Matrix< double, MATRIX_SIZE,  1> v_Nd;
    v_Nd = MatrixXd::Random( MATRIX_SIZE,1 );

    clock_t time_stt = clock(); // 计时
    // 直接求逆
    Matrix x = matrix_NN.inverse()*v_Nd;
    cout <<"time use in normal inverse is " << 1000* (clock() - time_stt)/(double)CLOCKS_PER_SEC << "ms"<< endl;
    
	// 通常用矩阵分解来求，例如QR分解，速度会快很多
    time_stt = clock();
    x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
    cout <<"time use in Qr decomposition is " <<1000*  (clock() - time_stt)/(double)CLOCKS_PER_SEC <<"ms" << endl;

    return 0;
}

 

---

3.3 旋转向量和欧拉角（都只是描述旋转）

我们希望有一种方式能够紧凑地描述旋转和平移。例如,用一个三维向量表达旋转,用六维向量表达变换。

对于坐标系的旋转,我们知道,任意旋转都可以用一个旋转轴和一个旋转角来刻画。于是,我们可以使用一个向量,其方向与旋转轴一致,而长度等于旋转角。这种向量,称为旋转向量。同样,对于变换矩阵,我们使用一个旋转向量和一个平移向量即可表达一次变换。这时的维数正好是六维。

旋转向量<-------->旋转矩阵

 

无论是旋转矩阵、旋转向量,虽然它们能描述旋转,但对我们人类是非常不直观的。而欧拉角则提供了一种非常直观的方式来描述旋转——它使用了三个分离的转角,把一个旋转分解成三次绕不同轴的旋转。假设一个刚体的前方(朝向我们的方向)为X 轴,右侧为 Y 轴,上方为 Z 轴,见图 3-3。那么,ZY X 转角相当于把任意旋转分解成三个轴上的转角。此时,我们可以使用 [r, p, y] T 这样一个三维的向量描述任意旋转。但是欧拉角的一个重大缺点是会碰到著名的万向锁问题(Gimbal Lock  )。

---

3.4 四元数(目前只讨论表示旋转）

旋转矩阵用九个量描述三自由度的旋转,具有冗余性;欧拉角和旋转向量是紧凑的,但具有奇异性。事实上,我们找不到不带奇异性的三维向量描述方式。四元数(Quaternion)是 Hamilton 找到的一种扩展的复数. 它既是紧凑的,也没有奇异性。如果说缺点的话,四
元数不够直观,其运算稍为复杂一些。

q = q 0 + q 1 i + q 2 j + q 3 k, 乘以 i 应该对应着旋转 180 度,这样才能保证 ij = k 的性质。而 i 2 = −1,意味着绕i 轴旋转 360 度后,你得到了一个相反的东西。这个东西要旋转两周才会和它原先的样子相等。

一个虚四元数对应到一个空间点，我们能用单位四元数表示三维空间中任意一个旋转。

旋转向量<-------->四元数

 

四元数<-------->旋转矩阵的转换

任意单位四元数描述了一个旋转,该旋转亦可用旋转矩阵或旋转向量描述。把四元数转换为矩阵的最直观方法,是先把四元数 q 转换为轴角 θ 和 n,然后再根据罗德里格斯公式转换为矩阵。不过那样要计算一个 arccos 函数,代价较大。

---

3.6 实践:Eigen 几何模块

实现各种变换的相关转换。

#include 
#include 
#include 
// Eigen 几何模块
#include 
using namespace std;
using namespace Eigen;

int main ( int argc, char** argv )
{
/********************* 旋转向量和和旋转矩阵***************/
/*********************
   初始化旋转向量和和旋转矩阵
**********************/
    // 3D 旋转矩阵使用 Matrix
    Matrix rotation_matrix = Matrix::Identity();
    // 旋转向量使用 AngleAxis(角度*向量）, 它底层不直接是Matrix，但运算可以当作矩阵（因为重载了运算符)
    AngleAxisd rotation_vector ( M_PI/4, Vector3d ( 0,0,1 ) );     //沿 Z 轴旋转 45 度
    cout .precision(3);
/*********************
   旋转向量和矩阵的转换
**********************/
    cout<<"1、rotation matrix =\n"< v ( 1,0,0 );
    Matrix v_rotated = rotation_vector * v;
    cout<<"(1,0,0) after rotation = "< v_transformed = T*v;                              // 相当于R*v+t
    cout<<"v tranformed = "<