【机器学习实战】线性回归----boston房价预测

不积跬步无以至千里，实践经验得慢慢积累，就从线性回归开始练习。

【导入所需要用到的库和数据分析】

导入库：

##用于可视化图表
import matplotlib.pyplot as plt
##用于做科学计算
import numpy as np
##用于做数据分析
import pandas as pd
##用于加载数据或生成数据等
from sklearn import datasets
##加载线性模型
from sklearn import linear_model
###用于交叉验证以及训练集和测试集的划分
from sklearn.cross_validation import train_test_split
from sklearn.model_selection import cross_val_predict
###这个模块中含有评分函数，性能度量，距离计算等
from sklearn import metrics

数据集：选择波士顿房价数据集，这是sklearn自带的小数据集，是一个用于回归任务的经典数据集。

boston = datasets.load_boston()
print(boston.data.shape)
print(boston["feature_names"])

输出为：
(506, 13)
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
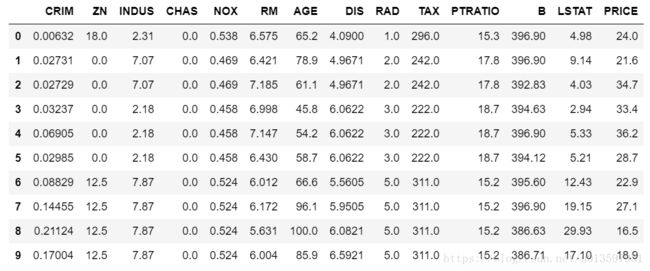
 'B' 'LSTAT']

我们可以了解到这个数据集中有506个样本，每个样本有13个输入特征，分别是：

feature	means
CRIM	城镇人均犯罪率
ZN	住宅用地超过25000sq.ft的比例
INUDS	城镇非零售商用土地的比例
CHAS	查理斯河空变量(如果边界是河流则为1，否则为0)
NOX	一氧化氮浓度
RM	住宅平均房间数
AGE	1940年之前建成的自用房屋比例
DIS	到波士顿五个中心区域的加权距离
RAD	辐射性公路接近指数
TAX	每10000美元的全值财产税率
PTRATIO	城镇师生比例
B	1000 (Bk−0.63)2 ( B k − 0.63 ) 2 ，其中 Bk B k 代表城镇中黑人的比例
LSTAT	人口中地位低下者的比例

除了这13个特征外，还有一个输出我们用PRICE表示房价。

获得数据集的输入和输出，并将它们放到一张表里来看：

boston_X = boston.data   ##获得数据集中的输入
boston_y = boston.target ##获得数据集中的输出，即标签(也就是类别)
boston_data = pd.DataFrame(boston_X)
boston_data.columns = data_boston.feature_names
boston_data["PRICE"]=boston_y
boston_data.head()

输出如下：

这么多特征我们可以选取其中几个来做训练。比如选取ZN，RM，PTRATIO，LSTAT作为输入特征，PRICE则是我们的输出

data_X=boston_data[['ZN','RM','PTRATIO','LSTAT']]
data_y=boston_data[['PRICE']]

【划分训练集与测试集】

我们通过设定test_size=0.1来设置测试集是占数据集的十分之一，我们可以打印看一看它们的数量：

### test_size:测试数据大小
X_train,X_test,y_train,y_test = train_test_split(data_X, data_y, test_size = 0.1)
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)

输出：
(455, 4)
(51, 4)
(455, 1)
(51, 1)

训练集有455个样本，测试集有51个样本。

【加载并训练模型】

sklearn中的线性回归模型LinearRegression()是使用最小二乘法来实现的。

##加载线性回归模型
model=LinearRegression()
##将训练数据传入开始训练
model.fit(X_train,y_train)

我们可以打印系数和截距来看看这四个特征和输出的关系，

print(model.coef_)     #系数，有些模型没有系数（如k近邻）
print(model.intercept_) #与y轴交点，即截距

输出：
[[-0.01759158  4.3701041  -0.94665828 -0.60046412]]
[ 20.27487956]

我们可以得到输出四个特征的关系:
y=−0.01759158x1+4.3701041x2−0.94665828x3−0.60046412x4+20.27487956 y = − 0.01759158 x 1 + 4.3701041 x 2 − 0.94665828 x 3 − 0.60046412 x 4 + 20.27487956

官网上还有提到Ridge Regression，我们也来试一试，它其实就是在最小二乘法的基础上对系数的L2范数的平方加了一个 λ λ 惩罚项。
对于普通的线性回归，我们的算法思路是： minw||wX−y||22 min w | | w X − y | | 2 2 此处为L2范数的平方 此 处 为 L 2 范 数 的 平 方
对于Ridge Regression，它的思路是： minw||wX−y||22+λ||w||22 min w | | w X − y | | 2 2 + λ | | w | | 2 2
我们导入Ridge Regression模型：

model_ridge=linear_model.Ridge(alpha = .5)
model_ridge.fit(X_train,y_train)
print(model_ridge.coef_)
print(model_ridge.intercept_)

输出：
[[-0.01757544  4.35451637 -0.94714198 -0.6012894 ]]
[ 20.39189661]

【模型评价】

对于回归模型的评价我们一般会用MSE(均方误差，mean-square error)，RMSE(均方根误差，root-mean-square error)，MAPE(相对百分误差绝对值的平均值，mean absolute percentage error)。
我们使用sklearn中的Metrics模块，这个模块中有评分函数，性能度量，距离计算等。
我们可以看看关于回归模型的评价方法有哪些，

这里我们使用MSE和RMSE来做模型评价。

y_pred = model.predict(X_test)
y_ridge_pred = model_ridge.predict(X_test)
print("使用LinearRegression模型的均方误差为:",metrics.mean_squared_error(y_test, y_pred))
print("使用LinearRegression模型的均方根误差为:",np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
print("使用Ridge Regression模型的均方误差为:",metrics.mean_squared_error(y_test, y_ridge_pred))
print("使用Ridge Regression模型的均方根误差为:",np.sqrt(metrics.mean_squared_error(y_test, y_ridge_pred)))

输出为：
使用LinearRegression模型的均方误差为: 17.480665476
使用LinearRegression模型的均方根误差为: 4.1809885764
使用Ridge Regression模型的均方误差为: 17.4959695065
使用Ridge Regression模型的均方根误差为: 4.18281836882

我们还可以使用一下交叉验证的方式来看一看：
cv=10，即将数据集分为10组(一般均分)，然后每次选择一组作为验证集，其余九组作为训练集。这样的交叉验证被称为k折交叉验证，这里k取10。

predicted = cross_val_predict(model, data_X, data_y, cv=10)
print("使用交叉验证的均方误差为:",metrics.mean_squared_error(data_y, predicted))

输出为：
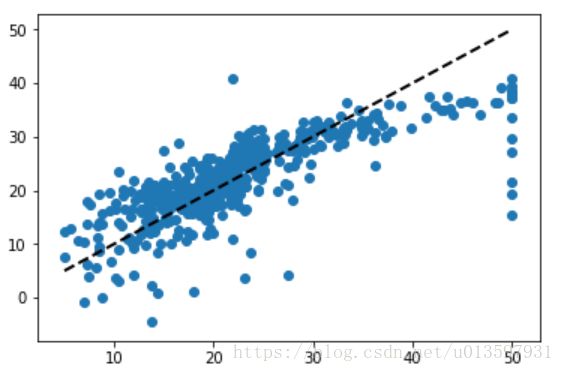
使用交叉验证的均方误差为: 33.0604706773

我们可以发现这里的均方误差比上面的大，那是因为上面只针对那10%的测试集求了MSE，而这里对每一折的测试集都求了MSE。

最后我们可以用图像来直观表示预测值与真实值的关系。

plt.figure('model')
plt.plot(data_y,predicted,'.')
plt.plot([data_y.min(),data_y.max()],[data_y.min(),data_y.max()],'k--',lw=2)
plt.scatter(data_y,predicted)
plt.show()

输出为：

离虚线越近的点误差越小。

参考：
http://scikit-learn.org/stable/modules/linear_model.html#ordinary-least-squares-complexity
http://www.cnblogs.com/pinard/p/6016029.html