算法导论——分治法——最大子数组问题
好久没有写博客了。以后我会不定期地写一些算法的博客,分享一些算法的感想。以下的说法很多都是我自己的感想,肯定有很多不足的地方,希望大家指正。
今天把算法导论里面分治法这一章里面的第一个问题——最大子数组问题写出来。另外这个问题的线性时间复杂度算法我也写了,在这里:http://blog.csdn.net/songxueyu/article/details/47005557
分治法,分而治之。对于一些问题,如果使用穷举法,时间复杂度可能不能接受,如n平方的时间复杂度。这时候使用分治法的话将会大大减少时间(尤其是在n比较大的情况下)。分有很多种分法,有的是二路,有的是三路。其实我觉得分治法的思想不难理解,想要为一个问题找出分治的解法,关键在于两个方面:1.怎么分,2.分了之后怎么找出一个时间复杂度可以接受的算法。这两个方面解决好了一个方面,一般就能得到一个可以接受的算法了。
比如说快速排序。它关注的是怎么分,它每次按照一个数组中的数为中心来分,然后再递归地对分好的子数组进行递归。
而归并排序关注的是分完了找出一个线性时间复杂度的算法。它的第一方面就只是简单地进行二路或者多路的划分,而对于这些划分进行归并才是这个算法中要解决的问题。因为对于很多问题我们都可以分,但是如何在分后进行治就比较难了。
最大子数组问题的分治法和归并排序一样,最重要地是在分了之后找到一个线性时间复杂度的算法来进行处理从而加快算法。这个算法在书中有说明,我这里就不再提了。
下面是JAVA代码:
package com.song.algorithm;
import java.util.Arrays;
public class FindMaxSubDoubleArray {
public static double MIN_VALUE = -10000000;
private static double[] work;
public static class Result{
public int start;
public int end;
public double max;
}
private static void generate_work(double[] a){
work = new double[a.length - 1];
for(int i = 1; i < a.length; i++){
work[i - 1] = a[i] - a[i-1];
}
System.out.println(Arrays.toString(work));
}
public static Result find(double[] a){
generate_work(a);
Result res = do_rec_find(0, work.length - 1);
res.end++;
return res;
}
private static Result do_rec_find(int start, int end){
if(start < end){
int mid = (start + end) / 2;
Result rl = do_rec_find(start, mid);
Result rh = do_rec_find(mid + 1, end);
Result rc = do_cross_find(start, mid, end);
if(rl.max >= rh.max && rl.max >= rc.max){
return rl;
}
if(rh.max >= rl.max && rh.max >= rc.max){
return rh;
}
if(rc.max >= rl.max && rc.max >= rh.max){
return rc;
}
}
Result res = new Result();
res.start = start;
res.end = start;
res.max = work[start];
return res;
}
private static Result do_cross_find(int start, int mid, int end){
double add = 0;
Result res = new Result();
double maxl = MIN_VALUE;
for(int i = mid; i >= start; i--){
add += work[i];
if(add > maxl){
res.start = i;
maxl = add;
}
}
double maxh = MIN_VALUE;
add = 0;
for(int i = mid + 1; i <= end; i++){
add += work[i];
if(add > maxh){
res.end = i;
maxh = add;
}
}
res.max = maxl + maxh;
return res;
}
/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
double[] a = {9,10,8,12,6,10,12,11,9,1};
//double[] a = {9,10,8,12,10,6,12,11,9,1};
System.out.println(Arrays.toString(a));
Result res = find(a);
System.out.println(res.start + " " + res.end + " " + res.max);
}
}
接下来递归调用do_rec_find。基本上和书上的一样。
但是在实现do_cross_find的时候我碰到了问题。一开始我没有按照书上的那样——第一个for循环从mid到start,而是第一个for循环从mid-1到start,然后在最后加上work[mid]。因为我觉得是要找出start到mid-1(包括)中最大的一段,再找出mid+1到end最大的一段,然后加上mid的值。OK,出错了,对于这样的数组
[1.0, -2.0, 4.0, -6.0, 4.0, 2.0, -1.0, -2.0, -8.0](生成的work数组)
得到的结果是4.0,开始位置是2,结束位置是2.为什么找不到6.0呢
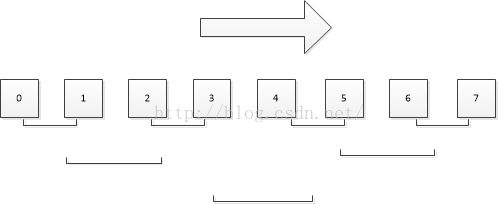
跟踪代码之后,发现分成0到4和5到8.
当0到4和5到8分别计算得到最大子数组后该计算cross了,如果按照我最先的实现,那么必须在0到3之间找到一个最大值然后在5到8找到一个最大值最后再加上4的值。而最终结果应该是4和5相加得到最大值,并不包括0到3中的值.
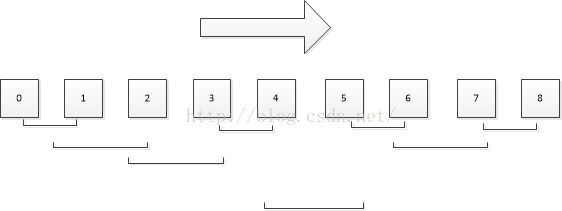
所以说第一个for应该从mid到start,这样可以允许不包括 好吧,那么第二个for呢?为什么就一定需要包括>mid的值呢? 这个问题确实值得思考,如果一个算法中不理解一些比较细的地方就根本不算是理解了。 首先如果n是偶数,由于索引从0开始,(n-1)/2是奇数(因为Java中是下取整的) 比如 我们看一下这个算法运行的过程,第一次分的时候mid是3. 首先是0,然后是1,然后是0和1,。 然后是2,是3,是2和3. 然后是4,是5,是4和5. 是6,是7,是6和7. 然后是0/1的结果和2/3的结果 然后是4/5的结果和6/7的结果 最后结果。 发现了什么? 这个算法是从左到右的。当算右边的最大子数组的时候左边的已经算好了。如果最大子数组是2和3,那么在算cross之前就已经算好了,如果是3和4,那么在cross的时候会算出来。 如果n是奇数。如 所以因为下取整的原因,mid总是位于左边,而算法是从左到右的,所以在算cross的时候,左边的情况(即 欢迎指正