第六章 -查找
1.下列叙述中,不符合m阶B树定义要求的是(D)。
-
根结点最多有m棵子树 -
所有叶结点都在同一层上 -
各结点内关键字均升序或降序排列 -
叶结点之间通过指针链接
解析:
选项A、B和C都是B-树的特点,而选项D则是B+树的特点。注意区别B-树和B+树各自的特点。
2.已知一个长度为16的顺序表L,其元素按关键字有序排列,若采用折半查找法查找一个 L中 不存在的元素,则 关键字的 比较次数最多是(B)
-
4 -
5 -
6 -
7
解析:16个二叉排序树的深度为5,查找一个不存在的最多查到最后一层,即5
3.为提高散列(Hash)表的查找效率,可以采取的正确措施是()。
Ⅰ.增大装填(载)因子
Ⅱ.设计冲突(碰撞)少的散列函数
Ⅲ.处理冲突(碰撞)时避免产生聚集(堆积)现象
-
仅Ⅰ -
仅Ⅱ -
仅Ⅰ、Ⅱ -
仅Ⅱ、Ⅲ
解析:
Hash表的查找效率取决于散列函数、处理冲突的方法和装填因子。显然,冲突的产生概率与装填因子(表中记录数与表长之比)的大小成正比,即装填得越满越容易发生冲突,Ⅰ错误。Ⅱ显然正确。采用合适的处理冲突的方式避免产生聚集现象,也将提高查找效率,例如用拉链法解决冲突时就不存在聚集现象,用线性探测法解决冲突时易引起聚集现象,Ⅲ正确。
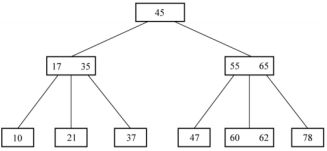
4.设有一棵3 阶 B 树,如下图所示。删除关键字 78 得到一棵新 B 树,其最右叶结点所含的关键字是( D)。
-
60 -
60, 62 -
62, 65 -
65
解析:详解:https://blog.csdn.net/v_JULY_v/article/details/6530142
在B-树叶结点上删除一个关键字的方法是:
首先将要删除的关键字 k直接从该叶子结点中删除。然后根据不同情况分别作相应的处理,共有三种可能情况:
(1)如果被删关键字所在结点的原关键字个数n>=ceil(m/2)(即向上取整),说明删去该关键字后该结点仍满足B-树的定义。这种情况最为简单,只需从该结点中直接删去关键字即可。
(2)如果被删关键字所在结点的关键字个数n等于ceil(m/2)-1,说明删去该关键字后该结点将不满足B-树的定义,需要调整。
调整过程为:如果其左右兄弟结点中有“多余”的关键字,即与该结点相邻的右(左)兄弟结点中的关键字数目大于ceil(m/2)-1。则可将右(左)兄弟结点中最小(大)关键字上移至双亲结点。而将双亲结点中小(大)于该上移关键字的关键字下移至被删关键字所在结点中。
对于本题,n=ceil(3/2)-1 。所以将做节点最大关键字62上移,同时将双亲结点中大于62的关键字(65)下移至删除结点位置。
5.用哈希(散列)方法处理冲突(碰撞)时可能出现堆积(聚集)现象,下列选项中,会受堆积现象直接影响的是 。
-
存储效率
-
散列函数
-
装填(装载)因子
-
平均查找长度
解析:产生堆积现象,即产生了冲突,它对存储效率、散列函数和装填因子均不会有影响,而平均查找长度会因为堆积现象而增大,选D 这题拉链法对存储没影响
6.在一棵具有15个关键字的4阶B树中,含关键字的结点个数最多是 。
-
5
-
6
-
10
-
15
解析:
关键字数量不变,要求结点数量最多,那么即每个结点中含关键字的数量最少。根据4阶B树的定义,根结点最少含1个关键字,非根结点中最少含⌈4/2⌉-1=1个关键字,所以每个结点中,关键字数量最少都为1个,即每个结点都有2个分支,类似与排序二叉树,而15个结点正好可以构造一个4层的4阶B树,使得叶结点全在第四层,符合B树定义,因此选D
7.下列选项中,不能构成折半查找中关键字比较序列的是 ()。
-
500,200,450,180
-
500,450,200,180
-
180,500,200,450
-
180,200,500,450
解析:注意是关键字比较序列,关键字的比较应该满足逻辑性
500,200,450,180
500
说明第一次比较结果是选择500之前的区间
200
说明第二次比较结果是选择200之后的区间
450
此时一定错了,因为只能在200-450的区间找数
180
8.已知字符串S为“abaabaabacacaabaabcc”,模式串t为“abaabc”。采用KMP算法进行匹配,第一次出现“失配”(s[i]≠t[j]) 时,i=j=5,则下次开始匹配时,i和j的值分别是
解析: 通过KMP算法知,i不变,j回退到首字母第一次相同的时候
9.在有n(n>1000)个元素的升序数组A中查找关键字x。查找算法的伪代码如下所示。
k=0;
while(k本算法与折半查找算法相比,有可能具有更少比较次数的情形是 。 B
-
当x不在数组中
-
当x接近数组开头处
-
当x接近数组结尾处
-
当x位于数组中间位置
解析:送分题。该程序采用跳跃式的顺利查找法查找升序数组中的x,显然是x越靠前,比较次数才会越少。
10.B+树不同于B树的特点之一是 。
-
能支持顺序查找
-
结点中含有关键字
-
根结点至少有两个分支
-
所有叶结点都在同一层上
解析:
由于B+树的所有叶结点中包含了全部的关键字信息,且叶结点本身依关键字从小到大顺序链接,可以进行顺序查找,而B树不支持顺序查找(只支持多路查找)
11.将关键字序列(7、8、30、11、18、9、14)散列存储到散列表中。散列表的存储空间是一个下标从0开始的一维数组,散列函数为H(key)=(key×3) mod 7,处理冲突采用线性探测再散列法,要求装填(载)因子为0.7。
1)请画出所构造的散列表。
2)分别计算等概率情况下查找成功和查找不成功的平均查找长度
解析:
1)由装载因子为0.7,数据总数为7,得一维数组大小为7/0.7=10,数组下标为0~9。所构造的散列函数值见表B-3。
表B-3
| key |
7 |
8 |
30 |
11 |
18 |
9 |
14 |
| H(key) |
0 |
3 |
6 |
5 |
5 |
6 |
0 |
采用线性探测再散列法处理冲突,所构造的散列表见表B-4。
表B-4
| 地址 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 关键字 |
7 |
14 |
|
8 |
|
11 |
30 |
18 |
9 |
|
表B-5
| key |
7 |
8 |
30 |
11 |
18 |
9 |
14 |
| 次数 |
1 |
1 |
1 |
1 |
3 |
3 |
2 |
故ASL成功=查找次数/元素个数=(1+2+1+1+1+3+3)/7=12/7。
这里要特别防止惯性思维。查找失败时,是根据查找失败位置计算平均次数,根据散列函数mod 7,初始只可能在0~6的位置。等概率情况下,查找0~6位置查找失败的查找次数见表B-6。
表B-6
| H(key) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
| 次数 |
3 |
2 |
1 |
2 |
1 |
5 |
4 |
故ASL不成功=查找次数/散列后的地址个数=(3+2+1+2+1+5+4)/7=18/7。
12. 设包含 4 个数据元素的集合 S={ "do", "for", " repeat", " while"},各元素的查找概率依次为: p1=0.35, p2 = 0.15, p3=0. 15, p4=0.35。将 S 保存在一个长度为 4 的顺序表中,采用折半查找法,查找成功时的平均查找长度为 2.2。请回答:
(1)若采用顺序存储结构保存 S,且要求平均查找长度更短, 则元素应如何排列? 应使用何种查找方法? 查找成功时的平均查找长度是多少?
(2)若采用链式存储结构保存 S,且要求平均查找长度更短,则元素应如何排列?应使用何种查找方法?查找成功时的平均查找长度是多少?
解析:
1)采用顺序存储结构,数据元素按其查找概率降序排列。
采用顺序查找方法。
查找成功时的平均查找长度= 0.35×1+0.35×2+0.15×3+0.15×4=2.1。
(2)【 答案一】
采用链式存储结构,数据元素按其查找概率降序排列,构成单链表。
采用顺序查找方法。
查找成功时的平均查找长度=0.35×1+0.35×2+0.15×3+0.15×4=2.1。
【答案二】
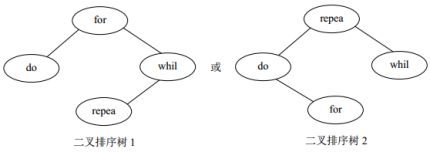
采用二叉链表存储结构,构造二叉排序树,元素存储方式见下图。
采用二叉排序树的查找方法。
查找成功时的平均查找长度=0.15×1+0.35×2+0.35×2+0.15×3=2.0