笔记-编译原理-第一章-第三章
编译原理学习笔记
第一章 引论
课程内容: 介绍程序设计语言 编译程序构造 的 基本原理 和 基本实现技术 。
1.1 什么是编译程序
翻译程序(Translator)
把某一种语言程序(称为 源语言程序) 等价 的转换成另一种语言程序(称为 目标语言程序) 的程序。
编译程序(Complier)
把某一种 高级语言程序 等价的转化成另一种 低级语言程序 (如汇编语言或机器语言程序)的程序。
编译程序可分为: 诊断编译程序、优化编译程序、交叉编译程序、可变目标编译程序 。
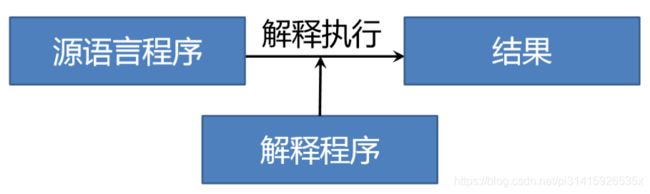
解释程序(Interpretor)
把 源语言 写的源程序作为输入,但不产生目标 程序,而是 边解释边执行 源程序。
1.2 为什么学习编译原理
从计算机科学与技术可以学到什么:
- 理解计算系统
- 设计计算系统
- 训练计算思维(Computational Thinking)
计算思维是什么:
计算思维是运用计算集科学的基础概念去求解问题,设计系统和理解人类行为。
计算思维的广泛方法:
抽象、自动化、问题分解、递归、权衡、保护、冗余、容错、纠错、和恢复、启发式等等。
1.3 编译过程
编译程序工作的五个阶段: 词法分析 、 语法分析 、 中间代码生成 、 优化 、 目标代码产生 。
词法分析
- 任务: 输入源程序,对构成源程序的字符串进行 扫描和分解,识别出单词符号
- 依循的原则:
构词规则 - 描述工具:
有限自动机
语法分析
- 任务:在词法分析的基础上,根据语法规则把 单词符号串分解成各类
语法单位(语法范畴) - 依循的原则:
语法规则 - 描述工具:
上下文无关文法
中间代码产生
- 任务:对各类语法单位按语言的语义进行初步翻译
- 依循的原则:
语义规则 - 描述工具:
属性文法 - 中间代码:
三元式,四元式,树,...
优化
- 任务:对前阶段产生的中间代码进行加工变换, 以期在最后阶段产生更高效的目标代码
- 依循的原则:
程序的等价变换规则
目标代码产生
- 任务: 把中间代码变换成特定机器上的目标代码
- 依赖于硬件系统结构和机器指令的含义
目标代码三种形式
- 汇编指令代码: 需要进行汇编
- 绝对指令代码: 可直接运行
- 可重新定位指令代码: 需要连接
可以直接运行的目标代码是绝对指令代码。
1.4 编译程序的结构
编译程序总框
出错处理
- 出错处理程序:发现源程序中的错误,把有关错误信息报告给用户
- 语法错误: 源程序中不符合语法(或词法)规则的错误;非法字符、括号不匹配、缺少;、…
- 语义错误: 源程序中不符合语义规则的错误 ;说明错误、作用域错误、类型不一致、…
遍(pass)
遍: 对源程序或源程序的中间表示 从头到尾扫描一次
阶段与遍是不同的概念
- 一遍可以由若干段组成
- 一个阶段也可以分若干遍来完成
编译前端与后端
- 与源语言有关,如词法分析,语法分析,语义分析与 中间代码产生,与机器无关的优化
编译后端
- 与目标机有关,与目标机有关的优化,目标代码产生
带来的好处
- 程序逻辑结构清晰
- 优化更充分,有利于移植
1.5 编译程序生成
以汇编语言和机器语言为工具
- 优点: 可以针对具体的机器,充分发挥计算机的系统 功能;生成的程序效率高
- 缺点: 程序难读、难写、易出错、难维护、生产的效 率低
高级语言书写
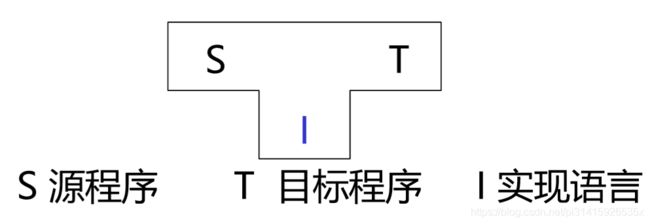
一个高级语言编写的编译器:
利用已有的某种语言的编译程序实现另一语言的编译程序
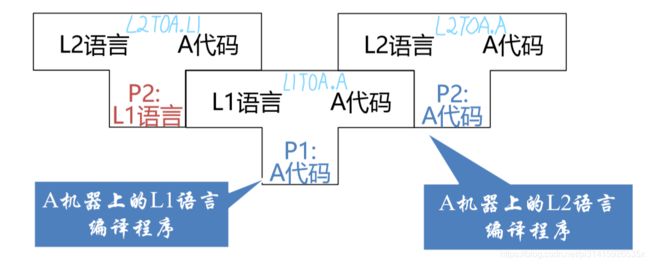
P1是一个可以在A机器上运行的编译程序(类似gcc.exe)即 L1ToA.A,可以将一个L1语言的代码编译成一个可以在A上运行的程序
这时我们用L1语言写一个编译L2语言的编译器P2,即 L2ToA.L1 为了能够在A机器上运行,所以我们需要上面的编译器来编译这个代码,得到 L2ToA.A 这样就得到了一个L2语言的编译器(例如我们用C++语言编写一个Python的编译器python.cpp,然后用g++.exe 编译链接得到一个可以运行的Python的编译器 python.exe)
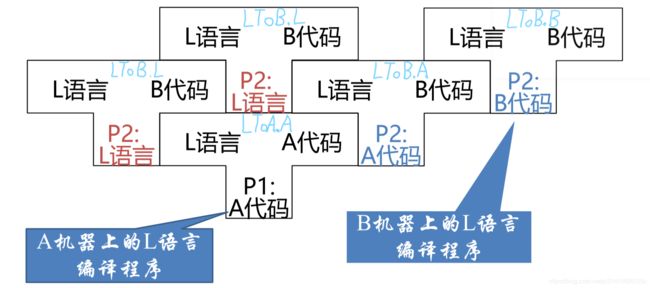
移植方法:把一种机器上的编译程序移植到另一种机器上
例如现在有一个在A平台(例如Windows)下的L语言(例如c++)的编译器,要移植这个编译器到B平台(Linux)下,我们拥有A平台下的一个L语言的编译器(例如g++.exe)即 LToA.A ,,
我们可以用L语言写一个针对B平台下的L语言的编译器(例如Linux中的g++.cpp)即 LToB.L ,
在A平台下编译即可得到一个在A平台下运行并可以编译出在B平台的下运行的L语言的编译器(P2: LToB.A)
然后再用这个A平台下的编译器编译我们的代码( LToB.L)就可以得到一个在B平台下运行的编译器 LToB.B
打个比方:
我们用c++ 编写一个 g++ForLinux.cpp 然后用 g++.exe 编译,得到 g++ForLinux.exe 然后用 g++ForLinux.exe 编译 g++ForLinux.cpp 就可以得到在Linux下运行的 g++ForLinux c++编译器了。
自编译方式
就是编写L的编译器就用L的一小部分 L 1 L_1 L1 写一个编译器,然后编译 L 1 + L 2 L_1 + L_2 L1+L2 得到一个较大的编译器,这样不断的重复下去,利用语言自己来写完整的编译器。
编译程序自动产生
编译程序-编译程序,编译程序产生器,编译程序书 写系统
LEX:词法分析程序产生器
YACC:语法分析程序产生器
第二章 高级程序设计语言概述
2.1 常用的高级程序设计语言
高级程序设计语言的优点
相对机器语言或汇编语言,高级程序设计语言
- 更接近于数学语言和工程语言,更直观、自然和易 于理解
- 更容易验证其正确性、改错
- 编写程序的效率更高
- 更容易移植
2.2 程序设计语言的定义
标识符是语法概念,名字是语义概念
程序语言的定义: 语法 、语义 、语用
语法
程序本质上是一定字符集上的字符串
语法:一组规则,用它可以形成和产生一个 合式(well-formed) 的程序。
词法规则 :单词符号的形成规则。
- 单词符号是语言中具有独立意义的最基本结构
- 一般包括:常数、标识符、基本字、算符、界符等
- 描述工具:有限自动机
语法规则 :语法单位的形成规则。
- 语法单位通常包括:表达式、语句、分程序、过程、 函数、程序等;
- 描述工具:上下文无关文法
语法规则 和 词法规则 定义了程序的形式结构。
定义语法单位的意义属于 语义 问题。
语义
语义 :一组规则,用它可以定义一个程序的意义 。
描述方法 :
- 自然语言描述:二义性、隐藏错误和不完整性
- 形式描述:操作语义 、指称语义 、代数语义
程序语言的基本功能和层次结构
程序,本质上说是描述一定数据的处理过程 。
程序语言的基本功能 :描述数据 和 对数据的运算 。
程序的层次结构
程序语言成分的逻辑和实现意义
- 抽象的逻辑的意义:数学意义
- 计算机实现的意义:具体实现
2.3 高级程序设计语言的一般特性
高级语言的分类
- 强制式语言(Imperative Languge)/过程式语言:命令驱动,面向语句,C、Pascal
- 应用式语言(Applicative Language): 注重程序所表示的功能,而不是一个语句接一个语 句地执行 LISP、ML
- 基于规则的语言( Rule-based Language): 检查一定的条件,当它满足值,则执行适当的动作 Prolog
- 面向对象语言(Object-Oriented Language): 封装、继承和多态性 Smalltalk,C++,Java
程序结构
- FORTRAN : 主程序段+辅程序段、没有嵌套和递归==> 模块化的特点
- PASCAL :程序本身可以看成是一个操作系统调用的过 程,过程可以嵌套和递归
- 作用域:一个名字能被使用的区域范围。
- 名字作用域规则—— "最近嵌套原则"
- JAVA :面向对象
数据结构与操作
数据类型 通常包括三要素:
- 用于区别这种类型数据对象的 属性
- 这种类型的数据对象可以具有的 值
- 可以作用于这种类型的数据对象的 操作
初等数据类型 : 数值类型 、逻辑类型 、字符类型、指针类型。
标识符与名字
标识符是语法概念,名字是语义概念
- 标识符:以字母开头的,由字母数字组成的字符串
- 名字:标识程序中的对象
名字的意义和属性 :
- 值:单元中的内容
- 属性:类型和作用域
名字的说明方式:
- 由说明语句来明确规定的
- 隐含说明
- 动态确定
数据结构
数组
n维矩形结构、长度可变和不可变、存放方式:按行存放、案列存放
数组元素地址计算:
记录
由已知类型的数据组合在一起的一种结构 (就是结构体。。。)
其中内部的元素也称为 域(field)
字符串、表格、栈
抽象数据类型
其内容包括:
- 数据对象集合
- 作用于这些数据对象的抽象运算的集合
- 这种类型对象的封装,即,除了使用类型中所定义 的运算外,用户不能对这些对象进行操作
程序设计语言对抽象数据类型的支持
语句与控制结构
表达式
- 表达式由 运算量(也称操作数,即数据引用或函数 调用) 和 算符(运算符,操作符) 组成 。
- 形式:中缀、前缀、后缀
- 表达式形成规则
算符的优先次序
一般的规定 :
- PASCAL:左结合A+B+C=(A+B)+C
- FORTRAN: 对于满足左、右结合的算符可任取一种
注意:
- 代数性质能引用到什么程度视具体的语言而定
- 在数学上成立的代数性质在计算机上未必完全成立(多个函数间的返回值的运算)
语句
- 赋值语句:左值->地址、右值->内容
- 控制语句 :无条件转移语句、条件语句 、循环语句、过程调用语句 、返回语句
语句的分类:
1.按功能:
- 执行语句:描述程序的动作
- 说明语句:定义各种不同数据类型的变量或运算, 定义名字的性质
2.按形式 :
- 简单句:不包含其他语句成分的基本句
- 复合句:句中有句的语句
第三章 高级程序设计语言的语法描述
3.1 上下文无关文法
文法
文法 :描述语言的语法结构的形式规则。
以英文句子: He gave me a book 举例:
语法描述的几个基本概念
- 字母表: 一个有穷字符集,记为 ∑ \sum ∑
- 字母表中每个元素称为 字符
- ∑ \sum ∑上的 字 (也叫 字符串) 是指由 ∑ \sum ∑ 中的字符所构成 的一个有穷序列
- 不包含任何字符的序列称为 空字 ,记为 ϵ \epsilon ϵ
- 用 ∑ ∗ \sum^* ∑∗ 表示 ∑ \sum ∑ 上的所有字的全体,包含空字 ϵ \epsilon ϵ
- 例如: 设 ∑ = { a , b } \sum = \{a, b\} ∑={a,b} ,则 ∑ ∗ = { ϵ , a , b , a a , a b , b a , b b , a a a , . . . } \sum^* = \{\epsilon,a,b,aa,ab,ba,bb,aaa,...\} ∑∗={ϵ,a,b,aa,ab,ba,bb,aaa,...}
- ∑ ∗ \sum^* ∑∗ 的子集 U U U 和 V V V 的
连接(积)定义为: U V = { α β ∣ α ∈ U & β ∈ V } UV = \{\alpha \beta|\alpha \in U \& \beta \in V \} UV={αβ∣α∈U&β∈V} ( α β \alpha \beta αβ 的连接有顺序) - V V V 自身的n次积为: V n = V V V ⋯ V ⏟ n V^n = \underbrace{VVV \cdots V}_{n} Vn=n VVV⋯V ,其中 V 0 = { ϵ } V^0 = \{\epsilon\} V0={ϵ};
- V ∗ V^* V∗ 是 V V V 的
闭包: V ∗ = V 0 ⋃ V 1 ⋃ V 2 ⋃ V 3 ⋯ V^*= V^0 \bigcup V^1 \bigcup V^2 \bigcup V^3 \cdots V∗=V0⋃V1⋃V2⋃V3⋯ - V + V^+ V+ 是 V V V 的
正规(则)闭包: V + = V V ∗ V^+=VV^* V+=VV∗
eg: 设 U = { α , α α } U=\{\alpha , \alpha \alpha\} U={α,αα} ,显然 U ∗ = { ϵ , a , a a , a a a , a a a a , … } U^*= \{ \epsilon, a, aa, aaa, aaaa, \ldots \} U∗={ϵ,a,aa,aaa,aaaa,…}
U + = { a , a a , a a a , a a a a , … } U^+=\{ a, aa, aaa, aaaa, \ldots \} U+={a,aa,aaa,aaaa,…}
闭包与正规闭包的区别: V V V 若无空字, V ∗ V^* V∗ 中有空字、而 V + V^+ V+ 无空字。
上下文无关文法
上下文无关文法 G G G 是一个四元组 G = ( V T , V N , S , P ) G=(V_T,V_N,S,P) G=(VT,VN,S,P),其中:
- V T V_T VT:
终结符(Terminal)集合(非空) - V N V_N VN:
非终结符(Noterminal)集合(非空),且 V T ⋂ V N = ∅ V_T \bigcap V_N= \emptyset VT⋂VN=∅ - S S S:文法的
开始符号, S ∈ V N S∈V_N S∈VN - P P P:
产生式集合(有限),每个产生式形式为 P 定 义 为 → α , P ∈ V N , α ∈ ( V T ⋃ V N ) ∗ P \underrightarrow{定义为} \alpha , P \in V_N, \alpha \in (V_T \bigcup V_N)^* P定义为α,P∈VN,α∈(VT⋃VN)∗ - 开始符S至少必须在某个产生式的左部出现一次
eg: 定义只含 + , ∗ +,* +,∗ 的算术表达式的文法 G = < { i , + , ∗ , ( , ) } , { E } , E , P > G=< \color{#F0A}{ \{i,+,*,(,)\} },\color{#0F5}{ \{E\} },\color{#08F}{E},\color{black}{P}> G=<{i,+,∗,(,)},{E},E,P>,其中,P 由下列产生式组成:
- E → i E \to i E→i ,
- E → E + E E \to E+E E→E+E
- E → E ∗ E E \to E*E E→E∗E
- E → ( E ) E →(E) E→(E)
巴科斯范式(BNF)
- “ → \to →” 用 “ : : = ::= ::=” 表示。
- 约定 { P → α 1 P → α 2 … p → α n 可 缩 写 为 ⟹ p → α 1 ∣ α 2 ∣ ⋯ ∣ α n \begin{cases} P \to \alpha_1 \\ P \to \alpha_2 \\ \ldots \\ p \to \alpha_ n \end{cases} 可缩写为\implies p \to \alpha_1 | \alpha_2 | \cdots | \alpha_n ⎩⎪⎪⎪⎨⎪⎪⎪⎧P→α1P→α2…p→αn可缩写为⟹p→α1∣α2∣⋯∣αn 其中 “ ∣ | ∣” 读成 ”或“ ,称 α i \alpha_i αi 为 P P P 的一个候选式, 故给出一个文法时将只给出
开始符号和产生式:如图:
G ( E ) G(E) G(E)里的 E E E 是指开始符号。
3.2 文法与语言
推导
定义: 称 α A β \alpha A \beta αAβ直接推出 α γ β αγβ αγβ,即 α A β ⟹ α γ β α \color{#F08}{A} \color{black}{β} \implies α \color{#F08}{γ} \color{black}{β} αAβ⟹αγβ 仅当 A → γ \color{#F08}{A→γ} A→γ 是一个产生式,且 α , β ∈ ( V T ∪ V N ) ∗ α,β∈(V_T ∪V_N)^* α,β∈(VT∪VN)∗。
如果 α 1 ⟹ α 2 ⟹ ⋯ ⟹ α n α_1 \implies α_2 \implies \cdots \implies α_n α1⟹α2⟹⋯⟹αn,则我们称这个序列是 从α1到αn的一个 推导 。若存在一个从 α 1 α_1 α1 到 α n α_n αn 的 推导,则称 α 1 α_1 α1 可以 推导 出 α n α_n αn。
对文法 G ( E ) : E → i ∣ E + E ∣ E ∗ E ∣ ( E ) G(E):E →i| E+E | E*E | (E) G(E):E→i∣E+E∣E∗E∣(E)
E ⟹ ( E ) ⟹ ( E + E ) ⟹ ( i + E ) ⟹ E ( i + i ) E \implies (E) \implies (E+E) \implies(i+E) \implies E(i+i) E⟹(E)⟹(E+E)⟹(i+E)⟹E(i+i)
句型、句子和语言
我们定义:
α 1 ⇒ ∗ α n \alpha_1 ⇒^* \alpha_n α1⇒∗αn 从 α 1 α_1 α1 出发,经过0步或若干步推出 α n α_n αn
α 1 ⇒ + α n \alpha_1 ⇒^+ \alpha_n α1⇒+αn 从 α 1 α_1 α1 出发,经过1步或若干步推出 α n α_n αn
因此, α ⇒ ∗ β \alpha ⇒^* \beta α⇒∗β 即为 α = β \alpha = \beta α=β 以及 α ⇒ + β \alpha ⇒^+ \beta α⇒+β
(这里的 + ∗ + * +∗ 都是在 ⇒ ⇒ ⇒ 的上面)
所以可以得到这样的关系,(理解一下即可):
< 句 子 > ⇒ ∗ He gave me a book < 句子>⇒^* \text{He gave me a book} <句子>⇒∗He gave me a book
< 句 子 > ⇒ + He gave me a book < 句子> ⇒^+ \text{He gave me a book} <句子>⇒+He gave me a book
He gave < 间接宾语><直接宾语> ⇒ + He gave me <冠词><名词> \text{He gave < 间接宾语><直接宾语>} ⇒^+ \text{He gave me <冠词><名词>} He gave < 间接宾语><直接宾语>⇒+He gave me <冠词><名词>
由以上定义可以得出句型、句子和语言的定义:
假定G是一个文法,S 是它的开始符号。
- 如果 S ⇒ ∗ α S⇒^* \alpha S⇒∗α,则称 α α α 是一个
句型 - 仅含终结符号的句型是一个
句子。 - 文法G所产生的句子的全体是一个
语言,记为 L ( G ) : L ( G ) = { α ∣ S ⇒ + α , α ∈ V T ∗ } L(G): L(G) = \{ \alpha | S ⇒^+ \alpha , \alpha \in V_T^* \} L(G):L(G)={α∣S⇒+α,α∈VT∗}
句型和句子练习
(这里为了排版更加的整齐(其实是打公式太懒)就贴图片了):
从文法到语言
从语言到文法
请给出产生语言为 { a n b n ∣ n ≥ 1 } \{a^nb^n|n≥1\} {anbn∣n≥1} 的文法:
G 3 ( S ) : G3(S): G3(S):
- S → a S b S →aSb S→aSb
- S → a b S →ab S→ab
3.3 语法树与二义性
推导与语法树
左推导和右推导
从一个句型到另一个句型的推导往往不唯一,从推导的方向看有两种:
- 最左推导:任何一步 α ⇒ β α⇒β α⇒β 都是对 α α α 中的中的左非 终结符进行替换
- 最右推导:任何一步 α ⇒ β α⇒β α⇒β 都是对 α α α 中的中的右非 终结符进行替换
语法树
- 用一张图表示一个句型的推导,称为
语法树 - 一棵语法树是不同推导过程的共性抽象
注意:
- 树中间,父子结点
可以同名 - 语法树不反应结点的产生先后顺序,只反映语法符号的定义或者说是构成关系
二义性(ambiguity)
文法的二义性:如果一个 文法 存在 某个句子 对应 两棵不同的语法树 ,则说这个文法是二义的 G ( E ) : E → i ∣ E + E ∣ E ∗ E ∣ ( E ) G(E):E →i|E+E|E*E|(E) G(E):E→i∣E+E∣E∗E∣(E) 是二义文法语言的二义性:一个语言是二义的,如果(那么) 对它不存在无二义的文法 。对于语言L,可能存在G和G’,使得 L ( G ) = L ( G ’ ) = L L(G)=L(G’)=L L(G)=L(G’)=L ,有可能其中一个文法为二义的, 另一个为无二义的
二义性问题是 不可判定问题 ,即不存在一个算法,它能在有限步骤内,确切地判定一个文法
对于是否是二义的 ,可以找到一组无二义文法的充分条件
3.4 形式语言鸟瞰
乔姆斯基于1956年建立形式语言体系,他把文 法分成四种类型:0,1,2,3型 。
- 0型(短语文法,图灵机):产生式形如: α → β α→β α→β ,其中: α ∈ ( V T ∪ V N ) ∗ α∈(V_T∪V_N)^* α∈(VT∪VN)∗且至少含有一个非终结符; β ∈ ( V T ∪ V N ) ∗ β∈ (V_T∪V_N)^* β∈(VT∪VN)∗
- 1型(上下文有关文法,线性界限自动机) :产生式形如: α → β α→β α→β ,其中: ∣ α ∣ ≤ ∣ β ∣ |α| ≤|β| ∣α∣≤∣β∣ ,仅 S → ε S→ε S→ε 例外
- 2型(上下文无关文法,非确定下推自动机) : 产生式形如: A → β A →β A→β ,其中: A ∈ V N ; β ∈ ( V T ∪ V N ) ∗ A∈V_N;β∈(V_T∪V_N)^* A∈VN;β∈(VT∪VN)∗ (可以利用栈分析)
- 3型(正规文法,有限自动机): 产生式形如: A → α B A →αB A→αB 或 A → α A →α A→α (右线性文法)其中:α∈VT*;A,B∈VN ;(左线性文法:产生式形如: A → B α A →Bα A→Bα 或 A → α A →α A→α )
四种类型文法描述能力比较
上下文无关文法
上下文有关文法
0型语言
程序设计语言不是上下文无关语言,甚至不是上下文有关语言,只能由0型语言产生,如:
习题
(end)