统计学习方法 第二章习题答案
文章目录
- 习题2.1
- 习题2.2
- 习题2.3
- 参考
习题2.1
题目:Minsky与Papert指出:感知机因为是线性模型,所以不能表示复杂的函数,如异或(XOR),验证感知机为什么不能表示异或。
答:即证明异或逻辑是线性不可分的
异或逻辑表
| x 1 x_{1} x1 | x 2 x_{2} x2 | y | label |
|---|---|---|---|
| 1 | 1 | 0 | -1 |
| 1 | 0 | 1 | +1 |
| 0 | 1 | 1 | +1 |
| 0 | 0 | 0 | -1 |
直观观察法:
将4个点投射到直角坐标系中

直观上可以发现,不能找到一条直线将两类点准确无误地分开,换言之,异或逻辑是线性不可分的。
数学证明(反证法):
当前训练集中含有4个点,其中正实例点为 x 1 = ( 1 , 0 ) T x_{1} = (1,0)^T x1=(1,0)T, x 2 = ( 0 , 1 ) T x_{2} = (0,1)^T x2=(0,1)T,负实例点为 x 3 = ( 1 , 1 ) T x_{3} = (1,1)^T x3=(1,1)T, x 4 = ( 0 , 0 ) T x_{4} = (0,0)^T x4=(0,0)T。
假设存在感知机模型 f ( x ) = sign ( w ⋅ x + b ) f(x)=\operatorname{sign}(w \cdot x+b) f(x)=sign(w⋅x+b)可以将两类点准确分类,其中 w = ( u , v ) T w = (u, v)^T w=(u,v)T,将 x 1 , x 2 , x 3 , x 4 x_{1}, x_{2}, x_{3}, x_{4} x1,x2,x3,x4代入,得:
{ 1 ∗ u + v ∗ 0 + b > 0 0 ∗ u + v ∗ 1 + b > 0 − ( 1 ∗ u + v ∗ 1 + b ) > 0 − ( 0 ∗ u + v ∗ 0 + b ) > 0 \left\{\begin{matrix} 1 * u+v*0+b >0\\ 0*u+v*1+b>0\\ -(1*u+v*1+b)>0\\ -(0*u+v*0+b)>0 \end{matrix}\right. ⎩⎪⎪⎨⎪⎪⎧1∗u+v∗0+b>00∗u+v∗1+b>0−(1∗u+v∗1+b)>0−(0∗u+v∗0+b)>0
化简得
{ u + b > 0 ① v + b > 0 ② u + v + b < 0 ③ − b > 0 ④ \left\{\begin{matrix} u+b>0\space\space①\\ v+b>0\space\space②\\ u+v+b<0\space\space③\\ -b>0\space\space④ \end{matrix}\right. ⎩⎪⎪⎨⎪⎪⎧u+b>0 ①v+b>0 ②u+v+b<0 ③−b>0 ④
①+②+④为 u + v + b > 0 u+v+b > 0 u+v+b>0,与③矛盾,所以不存在符合条件的感知机模型。
数学证明(迭代计算):
当前训练集中含有4个点,其中正实例点为 x 1 = ( 1 , 0 ) T x_{1} = (1,0)^T x1=(1,0)T, x 2 = ( 0 , 1 ) T x_{2} = (0,1)^T x2=(0,1)T,负实例点为 x 3 = ( 1 , 1 ) T x_{3} = (1,1)^T x3=(1,1)T, x 4 = ( 0 , 0 ) T x_{4} = (0,0)^T x4=(0,0)T。利用感知机学习算法的原始形式求感知机模型 f ( x ) = sign ( w ⋅ x + b ) f(x)=\operatorname{sign}(w \cdot x+b) f(x)=sign(w⋅x+b)。
利用 w ← w + η y i x i w \leftarrow w+\eta y_{i} x_{i} w←w+ηyixi, b ← b + η y i b \leftarrow b+\eta y_{i} b←b+ηyi进行迭代,其中取学习率 η = 1 \eta = 1 η=1。
取初值 w 0 = ( 0 , 0 ) T , b 0 = 0 w_{0} = (0,0)^T, b_{0} = 0 w0=(0,0)T,b0=0
| 迭代次数 | 误分类点 | w w w | b b b |
|---|---|---|---|
| 0 | - | ( 0 , 0 ) T (0,0)^T (0,0)T | 0 |
| 1 | x 1 x_{1} x1 | ( 1 , 0 ) T (1,0)^T (1,0)T | 1 |
| 2 | x 3 x_{3} x3 | ( 0 , − 1 ) T (0,-1)^T (0,−1)T | 0 |
| 3 | x 1 x_{1} x1 | ( 1 , − 1 ) T (1,-1)^T (1,−1)T | 1 |
| 4 | x 2 x_{2} x2 | ( 1 , 0 ) T (1,0)^T (1,0)T | 2 |
| 5 | x 3 x_{3} x3 | ( 0 , − 1 ) T (0,-1)^T (0,−1)T | 1 |
| 6 | x 2 x_{2} x2 | ( 0 , 0 ) T (0,0)^T (0,0)T | 2 |
| 7 | x 3 x_{3} x3 | ( − 1 , − 1 ) T (-1,-1)^T (−1,−1)T | 1 |
| 8 | x 1 x_{1} x1 | ( 1 , 0 ) T (1,0)^T (1,0)T | 2 |
| … | … | … | … |
迭代过程发生震荡(第8次的迭代结果与第4次一样,循环),因而不存在超平面可以将四类点准确分开。
习题2.2
题目:模仿例题2.1,构建从训练数据集求解感知机模型的例子。
答:习题2.1中的迭代计算的证明方法也是一个例子。
这里把例题2.1的实现代码写一下叭
# coding : utf-8
import numpy as np
def loadData():
X = np.mat([[3,3], [4,3], [1,1]]) #训练集X
Y = np.array([1,1,-1]) #对应的训练集标签
return X, Y
def train(X, Y, iter=15):
w = np.array([0 for i in range(X.shape[1])]) #设置w初值
b = 0 #设置b初值
eta = 1 #设置学习率
for i in range(15):
print("第%d次迭代, w="%i, w, "b=%d"%b)
flag = True #记录是否有数据误判
for j in range(len(Y)):
x = X[j]
y = Y[j]
#若有误判的数据
if y * (w*x.T + b) <= 0:
w = w + eta*y*x #更新w
b = b + eta*y #更新 b
flag = False
break
if flag:
break
return w, b
if __name__ == "__main__":
X, Y = loadData()
w, b = train(X, Y)
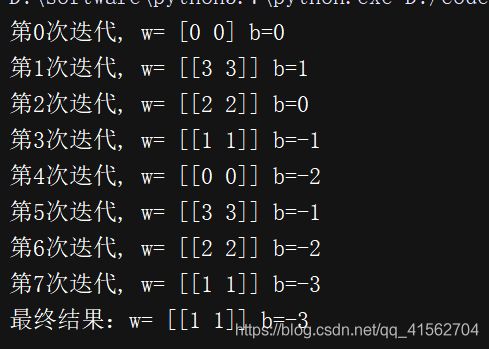
print("最终结果:w=", w, "b=%d"%b)
运行结果:
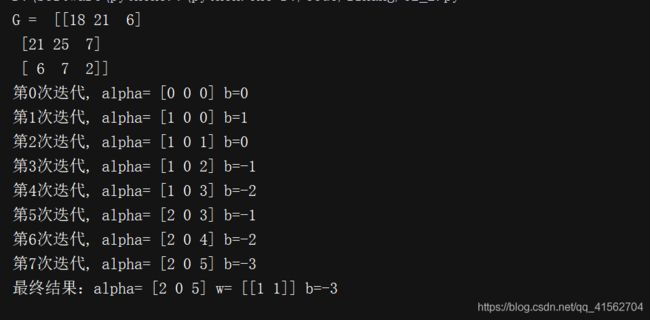
算法2.2是感知机学习的对偶形式,这里也实现一下
# coding : utf-8
import numpy as np
def loadData():
X = np.mat([[3,3], [4,3], [1,1]]) #训练集X
Y = np.array([1,1,-1]) #对应的训练集标签
return X, Y
def train(X, Y, iter=15):
N = X.shape[0]
#设置初值
alpha = np.array([0 for i in range(N)])
b = 0
eta = 1
#计算Gram矩阵
G = [[0] * N for i in range(N)]
for i in range(N):
for j in range(N):
G[i][j] = np.asarray(X[i]*X[j].T)[0][0]
G = np.mat(G)
print("G = ",G)
#迭代
for k in range(iter):
print("第%d次迭代, alpha="%k, alpha, "b=%d"%b)
flag = True
for i in range(N):
xi = X[i]
yi = Y[i]
#若有误判的数据
sum = np.sum(alpha*Y*np.asarray(G[i])) + b
if Y[i] * sum <= 0:
alpha[i] = alpha[i] + eta
b = b + eta*Y[i]
flag = False
break
if flag:
break
return alpha, b
if __name__ == "__main__":
X, Y = loadData()
alpha, b = train(X, Y)
w = Y * alpha * X
print("最终结果:alpha=", alpha, "w=", w, "b=%d" % b)
习题2.3
题目:证明以下定理:样本集线性可分的充分必要条件是正实例点集所构成的凸壳与负实例点集所构成的凸壳互不相交。
答:本题难点在于充分性的证明,尤其是如何根据已有的凸集构造超平面,充分性的证明也有一个凸集分离定理,对该定理证明感兴趣的可以参考文末的链接。先理解一下概念。
线性可分是指可以找到一个超平面将数据集中正实例点和负实例点准确地划分到超平面两侧。即对所有的正实例点有, w ⋅ x i + b > 0 w\cdot x_{i}+b > 0 w⋅xi+b>0,对所有的负实例点有 w ⋅ x i + b < 0 w\cdot x_{i}+b < 0 w⋅xi+b<0。
凸壳是指由范围内的点构成的多边形围成的区域。n维欧式空间中k个点的凸组合式一个凸集 { x = ∑ i = 1 k λ i x i ∣ x i ∈ R n , λ i ≥ 0 , ∑ i = 1 k λ i = 1 } \left\{x=\sum_{i=1}^{k} \lambda_{i} x_{i} | x_{i} \in \mathcal{R}^{n}, \lambda_{i} \geq 0, \sum_{i=1}^{k} \lambda_{i}=1\right\} {x=∑i=1kλixi∣xi∈Rn,λi≥0,∑i=1kλi=1}
必要性(线性可分->凸壳不相交):
假设样本集T线性可分,则存在一个超平面 w o p t w_{opt} wopt将数据集的正实例点和负实例点完全正确地划分到 w o p t w_{opt} wopt的两侧。
所有的正实例点满足 w ⋅ x i + b ≥ ε w \cdot x_{i}+b \geq \varepsilon w⋅xi+b≥ε,负实例点满足 w ⋅ x i + b ≤ ε w \cdot x_{i}+b \leq \varepsilon w⋅xi+b≤ε,其中 ε \varepsilon ε为无穷小量。
对正实例点构成的凸集中元素 x + x_{+} x+满足 w ⋅ x + + b = w ⋅ ∑ y i = 1 λ i x i + b = ∑ y i = 1 λ i ( w ⋅ x i + b ) = ε ∑ y i = 1 λ i > 0 \mathrm{w} \cdot x_{+}+b=\mathrm{w} \cdot \sum_{y_{i}=1} \lambda_{i} x_{i}+b=\sum_{y_{i}=1} \lambda_{i}\left(w \cdot x_{i}+b\right)=\varepsilon \sum_{y_{i}=1} \lambda_{i}>0 w⋅x++b=w⋅∑yi=1λixi+b=∑yi=1λi(w⋅xi+b)=ε∑yi=1λi>0,而对所有的负实例点构成的凸集中的元素 x − x_{-} x−满足 w ⋅ x − + b = w ⋅ ∑ y i = − 1 λ i x i + b = ∑ y i = − 1 λ i ( w ⋅ x i + b ) = ε ∑ y i = − 1 λ i < 0 \mathrm{w} \cdot x_{-}+b=\mathrm{w} \cdot \sum_{y_{i}=-1} \lambda_{i} x_{i}+b=\sum_{y_{i}=-1} \lambda_{i}\left(w \cdot x_{i}+b\right)=\varepsilon \sum_{y_{i}=-1} \lambda_{i}<0 w⋅x−+b=w⋅∑yi=−1λixi+b=∑yi=−1λi(w⋅xi+b)=ε∑yi=−1λi<0,显然正副凸集不相交。
充分性(凸壳不相交->线性可分):
凸壳不相交则根据凸集分离定理(在很弱的条件下,两个不相交的凸集总可用超平面分离),可以用超平面将两类点分离。
参考
第2章学习笔记
感知机:从原理到训练(包含第3题的证明)
凸壳与线性可分