几种AutoEncoder原理
AutoEncoder属于无监督学习的技术,其思想影响深远。
文章目录
- 1.经典 AutoEncoder
- 2.Denoising AutoEncoder
- 3.Sparse AutoEncoder
- 4.VAE
- 5. 卷积AutoEncoder
1.经典 AutoEncoder
Ref:Reducing the Dimensionality of Data with Neural Networks
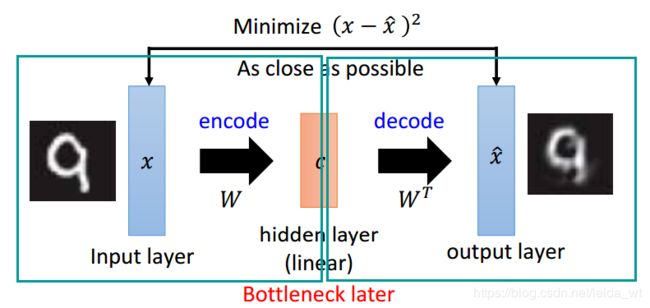
简单采用背靠背的全连接层,形成一个瓶颈neck就为经典AutoEncoder的架构核心,层数一般不多,以1或2层隐含层为主。其是与PCA做了相似的事情。
Hinton提出也可Deep起来
这里有趣之处是以RBM逐层初始化,然后穿起来Fine-tune。
此外这里的Encoder Decoder权重是共享的(仅取了转置),不过并不很重要。
结构如下所示
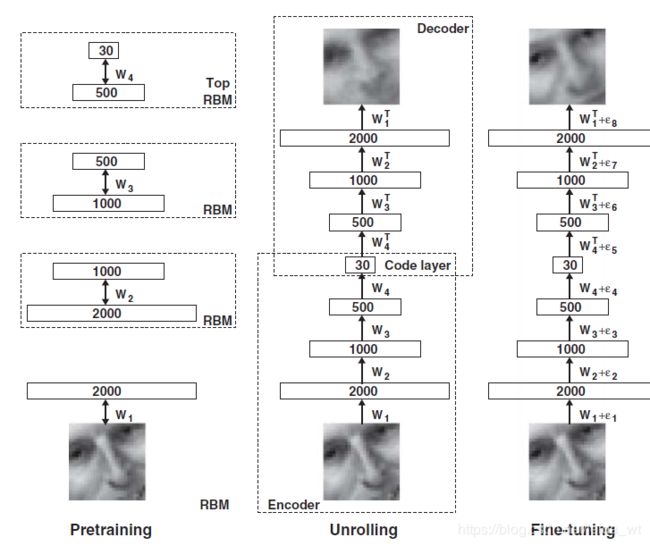
我实验发现直接使用relu激活加adam优化,在50000个MNIST数据集上跑,经10epochs就可达到较好的重建精度。
原图
重建
n.b. RBM及其训练
上述文章里训练每一层作为初始化时用到的RBM是一种经典的能量模型,(能量模型通俗解释https://www.zhihu.com/question/59264464),RBM很像但隐含层神经网络,但训练上区别很大,采用一种CD-K方法。
ref:https://wenku.baidu.com/view/7b9634e56bec0975f565e240.html
过程有点类似train一个单隐层AutoEncoder,参数有两个偏置项和一个链接权重项W,其目标函数F是依据能量背景提出的,优化目标是降低F,方法是梯度下降。比较有趣的地方是其是把概率p算出来后又取了采样(一般伯努利即可),使其变为0-1二值的。
RBM在relu,batchnorm等改善深度NN训练难题的技术普遍应用后,已经不再是必要的,而在06年左右,必需通过RBM逐层per-train才能train起来深度网路结构,故论文中还是应用了RBM。
通过可视化隐含层,可以证明AutoEncoder确实学到了表征
2.Denoising AutoEncoder
ref: Extracting and Composing Robust Features with Denoising Autoencoders
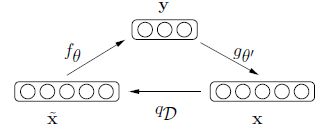
其思想很朴素,仅改动了一点:将输入数据加噪声(具体方法是随机把某些像素从0->1)后送进模型,然后期望恢复没有噪声的原始图像。通过这样的方法,作者认为能提取到更好更鲁棒性的表征。解释如下。
1.从流型学习角度解释
下图直观可认为,我们期望算法能把红圈内加噪声的x(由此偏离了原位置)推回去,这样的能力就有可能在处理与x的相似样本时有更好的泛化能力
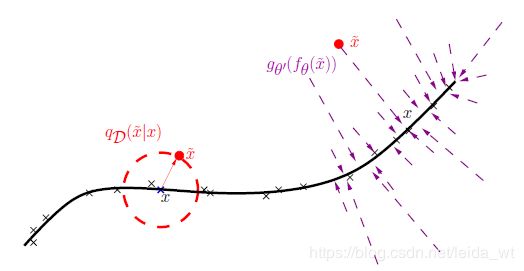
2.信息论观点解释(interesting)
这个AutoEncoder的工作可看做它把有噪声的的数据‘滤波’成了无噪声数据,使得信息量增加,这个增加正是来自‘滤波器’的注入,因此在训练时候隐含层参数就会保留(学习)到一些信息。因此最终的优化目标就可理解为在保留信息和尽可能最优化重建结果之间的权衡。
3.Sparse AutoEncoder
ref:
An Analysis of Single-Layer Networks in Unsupervised Feature Learning
http://deeplearning.stanford.edu/wiki/index.php/UFLDL教程
这个工作使用了新的Loss函数,在经典AE的Loss上加了稀疏惩罚项(sparsity penalty),即下图第二项

第二项展开为
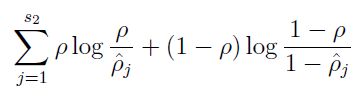
其中s2为隐含层s2的神经元个数,ρ为一个固定的超参数,表达稀疏程度,ρ_head为
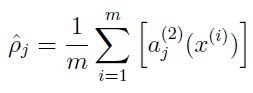
即在整个数据集上的平均激活度。
为了了解算法学到的特征,我们可以进行可视化,即寻找能最大化激活隐含层的输入图像(需要建立在某些约束条件下,比如约束图像像素和)。这里通过约束![]()
给出了能最佳激活第i个神经元的输入的解(其中xj是输入图像展开后的第j个像素)

具体的代码如下:
SAE稀疏自编码在MNIST数据集表现,进行10*10随机切割,不然可视化效果不明显。
import numpy as np
import matplotlib.pyplot as plt
import torch as t
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
from BasicModule import BasicModule
from tensorboardX import SummaryWriter
from sklearn.decomposition import PCA
writer = SummaryWriter('./runs/exp1')
t.manual_seed(1)
root = './AI/DataSets/MNIST'
batch_size = 32
data_spilt = 50000 # 截取的数据集大小,以减小计算量
inshape = (10, 10)
trainData = datasets.MNIST(root, transform=transforms.Compose([
transforms.RandomCrop(10),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)),
]))
trainData = t.utils.data.random_split(
trainData, [data_spilt, len(trainData)-data_spilt])[0]
train_loader = t.utils.data.DataLoader(
trainData, batch_size=batch_size, shuffle=True)
class SparseAutoEncoder(BasicModule):
def __init__(self, BETA=1, ROU=0.01, hiddenshape=300, USE_P=False):
super(SparseAutoEncoder, self).__init__()
self.model_name = 'SparseAutoEncoder'
self.BETA = BETA # 稀疏项考虑程度
self.ROU = ROU # 稀疏度
self.USE_P = USE_P
self.inshape = inshape[0]*inshape[1]
self.hiddenshape = hiddenshape
self.encoder = nn.Linear(self.inshape, self.hiddenshape)
self.decoder = nn.Linear(self.hiddenshape, self.inshape)
def forward(self, x):
encode = t.sigmoid(self.encoder(x))
decode = t.sigmoid(self.decoder(encode))
return encode, decode
def display_hidden(self, index):
with t.no_grad():
paras = [each for name,
each in self.encoder.named_parameters()] # w,b
w = paras[0]
num = w[index, :]
den = ((w[index, :]**2).sum())**0.5
plt.imshow((num/den).view(inshape).numpy())
plt.show()
def cal_hidden(self):
with t.no_grad():
paras = [each for name,
each in self.encoder.named_parameters()] # w,b
w = paras[0]
out = t.Tensor(w.shape[0], 1, inshape[0], inshape[1])
for i in range(w.shape[0]):
num = w[i, :]
den = ((w[i, :]**2).sum())**0.5
out[i, 0] = (num/den).view(inshape)
return out
def predict(self, x, load=None):
'''输入单张图片预测dataset元组(Tensor[1,28,28],class)
'''
self.eval()
with t.no_grad():
if load is not None:
self.load(load)
x, c = x
x = x.view(1, -1)
result = self(x)[1]
result = result.detach()
return x.view(inshape).numpy(), result.view(inshape).numpy()
def trainNN(self, lr=1, weight_decay=1e-5, epochs=5):
self.train()
optimizer = optim.Adam(
self.parameters(),
lr=lr,
weight_decay=weight_decay
)
batch_loss = 0
for epoch in range(epochs):
for i, (bx, by) in enumerate(train_loader):
bx = bx.view(bx.shape[0], -1)
optimizer.zero_grad()
criterion = nn.MSELoss() # mse损失
encode, decode = self(bx)
p_head = encode.sum(dim=0, keepdim=True)/encode.shape[0]
p = t.ones(p_head.shape)*self.ROU
penalty = (p*t.log(p/p_head)+(1-p) *
t.log((1-p)/(1-p_head))).sum()/p.shape[1]
if self.USE_P:
loss = criterion(decode, bx) + \
self.BETA*penalty
else:
loss = criterion(decode, bx)
loss.backward()
batch_loss += loss.item()
optimizer.step()
if epoch % 1 == 0:
print('batch loss={}@epoch={}'.format(batch_loss, epoch))
batch_loss = 0
为方便,训练和可视化部分代码在jupyter进行,代码如下
%load_ext autoreload
%autoreload 2
import SparseAutoEncoder2
from SparseAutoEncoder2 import SparseAutoEncoder as SAE
t.manual_seed(1)
model = SAE(BETA=5.0, ROU=0.01, hiddenshape=100,USE_P=True)
model.trainNN(lr=0.001, weight_decay=0, epochs=15)
from torchvision.utils import make_grid,save_image
hidden=model.cal_hidden()
res=make_grid(hidden,normalize=True, scale_each=False)
model.show(res)
save_image(hidden,normalize=True,filename='./hidden.png')
不加稀疏约束的隐含层激活状态,可看到很混乱,不含有明显的分工

加入稀疏约束项后明显改善,可看到隐含层较好的提取到了各个笔画的特征

接下来我试着在输入图片加一点噪声看看是否稀疏约束对降噪性能会有帮助。因为注意到不加约束的时候,算法对抹去大面积空白处的盐粒噪声很积极,反而对有数字区域不敏感,感觉加一点稀疏约束会有帮助,因为稀疏约束让隐含层更有效的捕获有价值信息,而非仅有白噪声区域。实验证明确实会略好一些,能恢复更多些的细节,进一步体现了稀疏约束的有效。

4.VAE
原文:
Auto-Encoding Variational Bayes
解读:
https://zhuanlan.zhihu.com/p/22464764
https://zhuanlan.zhihu.com/p/34998569
近期进展:
https://zhuanlan.zhihu.com/p/52676826?utm_source=qq&utm_medium=social
VAE相对较新,是一种生成模型,常用于生成图片。核心优势是其生成图片可控性好,可通过code控制,缺点是生成的图像较为模糊,内容不清晰,相比之下GAN能生成更清晰的图像。
其核心架构仍是Encode-Decode,但在中间加了code模糊化的环节。
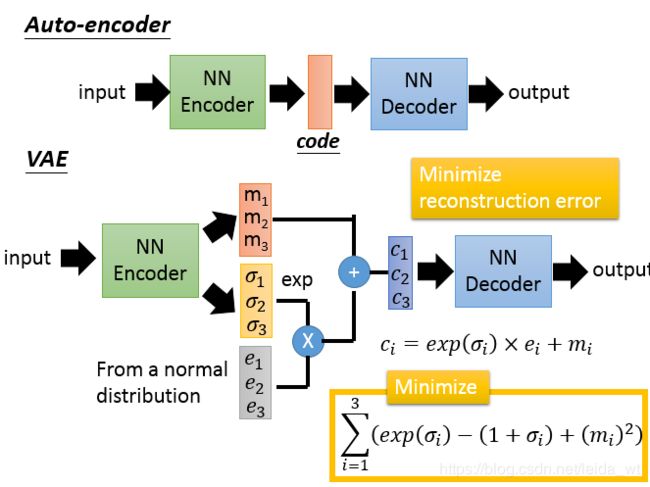
直觉上可如下理解:code有一定噪声区域时,就有更大的机会产生基于训练样本的新图片。如下:

故,虽然VAE推导较为复杂,但其最终实现是及其简洁的,两个NN,以重构精度和约束(结构图黄色框内,显然若无约束,NN会为了重构精度将所有噪声都设为0)为优化目标,然后进行标准的SGD即可训练。至于约束目标的来历,是较为精彩和复杂的。下面描述之
首先,有两大类学习模型:生成模型(Generative Model)和判别模型(Discriminative Model)
直接学习决策函数Y=f(X)或者条件概率分布P(Y|X)作为预测的模型
而生成模型基本思想是首先建立样本的联合概率概率密度模型P(X,Y),然后通过P(Y|X)= P(X,Y)/ P(X)得到P(Y|X)
故VAE的核心是:
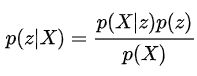
z是一些隐含变量,这在生成模型里经常出现,表达着一系列抽象特征。
这个式子在有些情况下是很好求解的,如在朴素贝叶斯分类器中,实现的是下式:

其中p(ci)是i类在数据集的占比,(数一下就可,易),p(x|ci)是从数据集所有的标记为i的数据中,抽出x的概率(假想为多元高斯的概率密度函数(PDF)),p(ci|x)即x属于ci的概率(求解目标)
但这里,由于p(X)是连续的,即有无穷多class,故加法变为下面的积分,并不好求

为此,提出了一种方法直接近似出p(z|X),这里的解决方法很经典,称之为Variational Inference。
可参考 http://blog.huajh7.com/2013/03/06/variational-bayes/
这里提出q(z)逼近之,以KL散度为判断标准
不难整理出下式(代入贝叶斯公式,KL散度公式):
![]()
接下来的大部分工作就是处理右边来转换这个优化目标。
观察之,为使得KL(q|p)最小,考虑到log(p(X))是个未知的常数,故,期望右一小,右二大。
至此都是相对常规化的内容,下面进入VAE论文的核心Reparameterization Trick,解释见 https://zhuanlan.zhihu.com/p/22464768 通过此技巧换z=g(X+e),e为随机变量,同时有q(z)=p(e),带入有
![]()
这一步前进了一大步,可以看到q(z|X)出现了。进一步,对右边第二项KL散度里两个分布均假设为标准高斯分布,即令q(…)=N(miu,sigma),p(z)=N(0,I)便可化简为
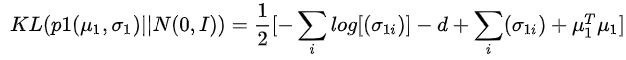
用NN吐出这个复杂的q的均值和方差,这就是ENCODER(重要思想,用NN代替难以计算和表达的复杂函数),其优化loss就是上面式子。实际实现有个细节就是吐出 logσ^2 而不是方差,因为方差只有正。同时注意到正是假设了p(z)为标准高斯,形成先验分布,才保证了优化中不会产生方差都变0的退化。
至此就给出了q的具体计算和其loss目标。
右边第一项即表达的是p(X|z)的对数似然,即DECODER的loss目标。VAE没有对DECODER进行假设,实现上直接由NN进行z->X_head的重建,以X X_head之间的BCE loss进行优化,与其他AutoEncoder一样。
实现:
pytorch官方有实现 https://github.com/pytorch/examples/tree/master/vae
其核心model为:
class VAE(nn.Module):
def __init__(self):
super(VAE, self).__init__()
self.fc1 = nn.Linear(784, 400)
self.fc21 = nn.Linear(400, 20)
self.fc22 = nn.Linear(400, 20)
self.fc3 = nn.Linear(20, 400)
self.fc4 = nn.Linear(400, 784)
def encode(self, x):
h1 = F.relu(self.fc1(x))
return self.fc21(h1), self.fc22(h1)
def reparameterize(self, mu, logvar):
std = torch.exp(0.5*logvar)
eps = torch.randn_like(std)
return eps.mul(std).add_(mu)
def decode(self, z):
h3 = F.relu(self.fc3(z))
return torch.sigmoid(self.fc4(h3))
def forward(self, x):
mu, logvar = self.encode(x.view(-1, 784))
z = self.reparameterize(mu, logvar)
return self.decode(z), mu, logvar
def loss_function(recon_x, x, mu, logvar):
BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784), reduction='sum')
KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
return BCE + KLD
大致运行情况:
重建情况

decoder对随机输入的输出,可看到VAE的特点,大概意思对,但并不清晰

5. 卷积AutoEncoder
ref: Stacked Convolutional Auto-Encoders for Hierarchical Feature Extraction
https://github.com/L1aoXingyu/pytorch-beginner/blob/master/08-AutoEncoder/conv_autoencoder.py
思路是将卷积加到AE架构中,改善了解决图像问题的性能,利用了CNN不会权重爆炸等一系列优点。核心是 反卷积 和 反池化怎么实现。(原论文通过使用发现maxpooling池化效果较好,其解释是max起到一种稀疏约束)
反池化很简单,非最大的部分全置零即可
pytorch实现有maxunpool层,但其需要maxpool层额外返回记录最大值索引的矩阵,比较麻烦,故这里就不采用,直接用反卷积卷回去也不错

反卷积实际就是再做一次卷积即可(通过补零,信号与系统典型套路)
pytorch实现有ConvTranspose2d层

实现
用MNIST_FASHION来做实验,MNIST_FASHION细节更丰富,同时计算量较小
import numpy as np
import matplotlib.pyplot as plt
import torch as t
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
from BasicModule import BasicModule
from torchvision.utils import make_grid, save_image
# 加噪声的SAE
t.manual_seed(1)
# root = ./AI/DataSets/MNIST'
root = './AI/DataSets/MNIST_FASHION'
batch_size = 32
data_spilt = 50000 # 截取的数据集大小,以减小计算量
inshape = (28, 28)
trainData = datasets.FashionMNIST(root, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
]))
trainData = t.utils.data.random_split(
trainData, [data_spilt, len(trainData)-data_spilt])[0]
train_loader = t.utils.data.DataLoader(
trainData, batch_size=batch_size, shuffle=True)
class ConvAutoEncoder(BasicModule):
def __init__(self):
super(ConvAutoEncoder, self).__init__()
self.model_name = 'ConvAutoEncoder'
self.encoder = nn.Sequential(
nn.Conv2d(1, 16, 3, stride=3, padding=1), # b, 16, 10, 10
nn.ReLU(True),
nn.MaxPool2d(2, stride=2), # b, 16, 5, 5
nn.Conv2d(16, 8, 3, stride=2, padding=1), # b, 8, 3, 3
nn.ReLU(True),
nn.MaxPool2d(2, stride=1) # b, 8, 2, 2
)
self.decoder = nn.Sequential(
nn.ConvTranspose2d(8, 16, 3, stride=2), # b, 16, 5, 5
nn.ReLU(True),
nn.ConvTranspose2d(16, 8, 5, stride=3, padding=1), # b, 8, 15, 15
nn.ReLU(True),
nn.ConvTranspose2d(8, 1, 2, stride=2, padding=1), # b, 1, 28, 28
nn.Tanh()
)
def forward(self, x):
encode = self.encoder(x)
decode = self.decoder(encode)
return encode, decode
def predict(self, x, load=None):
'''输入单张图片预测dataset元组(Tensor[1,28,28],class)
'''
self.eval()
with t.no_grad():
if load is not None:
self.load(load)
x, c = x
x = t.unsqueeze(x, 0) # (1,28,28) ->(1,1,28,28)
result = self(x)[1]
result = result.detach()
return x.view(inshape).numpy(), result.view(inshape).numpy()
def show(self):
def showim(img):
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)), interpolation='nearest')
plt.show()
for i, (bx, by) in enumerate(train_loader):
img_in = make_grid(bx, normalize=True)
showim(img_in)
self.eval()
with t.no_grad():
img_out = (self(bx)[1]).detach()
img_out = make_grid(img_out, normalize=True)
showim(img_out)
break
def trainNN(self, lr=1, weight_decay=1e-5, epochs=10):
self.train()
optimizer = optim.Adam(
self.parameters(),
lr=lr,
weight_decay=weight_decay
)
batch_loss = 0
for epoch in range(epochs):
for i, (bx, by) in enumerate(train_loader):
optimizer.zero_grad()
criterion = nn.MSELoss() # mse损失
encode, decode = self(bx)
loss = criterion(decode, bx)
loss.backward()
batch_loss += loss.item()
optimizer.step()
if epoch % 1 == 0:
print('batch loss={}@epoch={}'.format(batch_loss, epoch))
batch_loss = 0
训练
import numpy as np
import matplotlib.pyplot as plt
import ConvAutoEncoder
from ConvAutoEncoder import ConvAutoEncoder as CAE
model=CAE()
model.trainNN(lr=0.003, weight_decay=1e-5, epochs=18)
x,y=model.predict(ConvAutoEncoder.trainData[0])
plt.imshow(x)
plt.show()
plt.imshow(y)
plt.show()
model.show()

