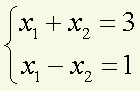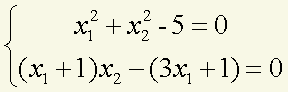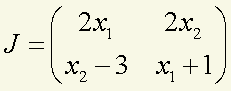R语言解线性方程组和求极值
1、R语言矩阵函数
t(x) 转置
diag(x) 对角阵
x %*% y 矩阵运算
solve(a,b) 运算a%*%x=b得到x
solve(a) 矩阵的逆
rowsum(x) 行加和
colsum(x) 列加和
rowMeans(x) 行平均
colMeans(x) 列平均2、求解线性方程组
分析:使用函数solve(a,b),运算a%*%x=b得到x。
a<-matrix(c(1,1,1,-1),2,2);
b<-c(3,1);
solve(a,b)
运行结果
> a<-matrix(c(1,1,1,-1),2,2);b<-c(3,1);solve(a,b)
[1] 2 1
a<-matrix(c(1,1,1,-1),2,2);
b<-c(3,1);
solve(a,b)
运行结果
> a<-matrix(c(1,1,1,-1),2,2);b<-c(3,1);solve(a,b)
[1] 2 1
注:这里矩阵a从数组读数是按照列读数
3、求解非线性方程组
解:先求Jacob行列式(求偏导)
相应的程序(程序名为:Newtons.R)为
Newtons<-function(fun,x,ep=1e-5,it_max=100){
index<-0;k<-1;
while(k编写求方程的程序(程序名为:funs.R)为
funs<-function(x){
f<-c(x[1]^2+ x[2]^2-5, (x[1]+1)*x[2]-(3*x[1]+1))
J<-matrix(c(2*x[1], 2*x[2],x[2]-3, x[1]+1),nrow=2,byrow=T)
list(f=f,J=J)
}
在这个函数中,输入变量是x,函数内部,f表示所有方程左边的函数,J是相应的Jacob矩阵.
输出变量有:函数值和相应的Jacob矩阵。
下面求解方程。
>Newtons(funs,c(0,1))
$root
[1] 1 2
$it
[1] 6
$index
[1] 1
$FunVal
[1] 1.598721e-14 6.217249e-15
即方程的解x*=(1,2)T,总共迭代了6次。
4、一元函数求极值
极大似然估计可以通过求对数似然方程的根得到,也可以直接求(对数)似然函数的极值得到。
loglike<-function(p)sum(log(1+(x-p)^2));
out<-optimize(loglike,c(0,5))
out
$minimum 极小点的近似解
[1] 0.9941774
$objective 目标函数在近似解处的函数值
[1] 1345.523
optimize(f, interval, ..., lower = min(interval),
upper = max(interval), maximum = FALSE, tol = .Machine$double.eps^0.25)
f----目标函数
interval=c()包含极小值区间
maximum = FALSE 表示求函数的极小值;TRUE表示求极大值
tol=精度
当未知参数是多元变量时,函数求极值的数值方法要采用多变量函数方法。
(1)可以用Newtons方法求解导函数方程;
(2)可以用nlm()函数直接求解无约束问题。
学出目标函数(程序名:Rosenbrock.R)
obj<-function(x){
f<-c(100*(x[2]-x[1]^2),1-x[1]);sum(f^2)
}
#source(“Rosenbrock.R")
x0<-c(-1.2,1);nlm(obj,x0)
输出结果:
$minimum
[1] 3.973766e-12
$estimate
[1] 0.999998 0.999996
$gradient
[1] -6.539256e-07 3.335987e-07
$code
[1] 1
$iterations
[1] 23
$minimum是函数的最优目标值
[1] 3.973766e-12
$estimate是最优点的估计值
[1] 0.999998 0.999996
$gradient是最优点处目标函数梯度值
[1] -6.539256e-07 3.335987e-07
$code是指示值,1表示迭代成功
[1] 1
$iterations是迭代次数
[1] 23