ACM6月月赛题解

（题解均为C++代码，建议大家用codeblocks运行。）
A
斐波那契数列，寻找规律即可，后一项为前两项之和。因为数据量不大所以递推即可。
AC代码如下：

#include
#include
#include 
#include
#include
#include
#include
#include
#include
#include
#include 
#define ll long long
using namespace std;
const int mod=1e9+7;
int main()
{
    int n;
    ll a=1,b=1,c=1;
    cin>>n;
    for(int i=2;i<n;i++)
    {
        c=(a+b)%mod;//中间mod防止爆int
        a=b%mod;
        b=c;
    }
    cout<<c<<endl;
    return 0;
}

B
此题简化后，求的是：从1~n中取k个数，使这k个数的最大公约数最大
因为两个数成倍数关系时，它们的最大公因数是两数中的较小数，也就是相对来说最大公因数较大
返回题目，这k个数其实就是：x1,x2…xk，及x的1~k倍，但必须保证xk小于n，在上述条件下，能知道，符合条件的最大的x就是答案，为了找出最大的x，必须使x*k尽量接近n，因为c++的整数除法有自动取整的功能，所以所有情况下，n/k都是最终答案（注意数据范围需要开long long ）
AC代码如下：

#include
#include
#include 
#include
#include
#include
#include
#include
#include
#include
#include 
#define ll long long //宏定义long long 
using namespace std;
int main()
{
    ll n,k;
    cin>>n>>k;
    cout<<n/k<<endl;
    return 0;
}

C
每个地方修复的时间，只要是比前面一个区域修复时间短，在修复前面一个区间的时候就能顺手把此区间修复，如果比前面区间修复时间长，在修复前面区间的时候也能修复后面一个区间，那么修复此区间的时间只需要d[i]-d[i-1]，以此来算出最短修复时间，跟TT获取驾照的时间一比结果就出来了。
AC代码为：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
int main()
{
    //priority_queuea;
    int n,a,b=0,c;
    int sum=0;
    scanf("%d",&n);
    while(n--)
    {
        scanf("%d",&a);
        if(a>b)
        {
            sum+=(a-b);
        }
        b=a;
    }
    scanf("%d",&c);
    if(c>=sum)
        printf("YES\n");
    else
        printf("NO\n");
    return 0;
}

D
此题考查的是对于2进制的掌握，
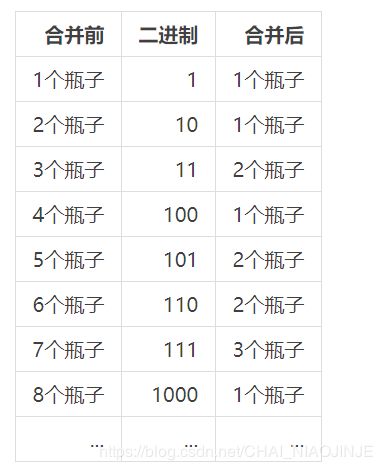由此图可知求合并后瓶子的个数可以直接转化为求该数2进制上1的个数
AC代码为：

#include
#include
#include 
#include
#include
#include
#include
#include
#include
#include
#include 
#define ll long long
using namespace std;
int main()
{
    int n,sum=0,k;
    cin>>n;
    while(n)
    {
        if(n%2==1)
        {
            sum++;
        }
        n/=2;
    }
    cout<<sum<<endl;
    return 0;
}

E
思路
模拟题。主要考察对三角函数的运用。
观察发现三角形在数轴上运动时，o点运动距离为s1,s2,0,s1,s2,0…交替。
算出s1,s2即可。
AC代码为：

#include//C++万能头文件
typedef long long ll;
const double pi=3.141592654;//定义PI
ll mod=998244353;
const ll inf=0x3f3f3f3f3f3f;//定义无穷大
using namespace std;
struct point
{
    double x,y;
}p[4];//保存O,A,B点的坐标
int main()
{
    double a,b,c;//OB,OA,AB的距离
    for (int i = 0; i < 3; i++)
        cin>>p[i].x>>p[i].y;
    b=sqrt(pow((p[0].x-p[1].x),2)+pow(p[0].y-p[1].y,2));//OA
    a=sqrt(pow((p[0].x-p[2].x),2)+pow(p[0].y-p[2].y,2));//OB
    c=sqrt(pow((p[2].x-p[1].x),2)+pow(p[2].y-p[1].y,2));//AB
    double A,B;
    A=acos((c*c+b*b-a*a)/(2*b*c));//∠A 的值
    B=acos((a*a+c*c-b*b)/(2*a*c));//∠B 的值
    double s1,s2;
    s1=a*(pi-B);//第一段的距离
    s2=b*(pi-A);//第二段的距离
    int n;cin>>n;
    double sum=0;
    int m=n%3;
    if(m==1) sum+=s1;//如果余数为1,加上第一段
    else if(m==2) sum+=s1+s2;//为2第一段和第二段都要
    printf("%.0f",(n/3)*(s1+s2)+sum);//四舍五入保留整数位并输出

}

F
本题属于防AK题型与上面的题目难度差距较大，没有接触过的人不太能够想出来。
斐波拉契 （hard version） 知识点 （矩阵快速幂）
注意到与easy version的区别在与n的范围，因为n<=1e9，故递推式o(n)会超时。
对于加速递推式的通用方法是矩阵快速幂，这能使得该问题在o(log2n）解决。
矩阵快速幂的最重要一步是构造常数矩阵，从而得到转移矩阵。
AC代码如下：

#include 

using namespace std;
typedef long long ll;
typedef vector<vector<ll>> mat;
int mod=1e9+7;
mat mul(mat &A,mat &B) //矩阵乘法
{
    mat C(A.size(),vector<ll>(B[0].size()));
    for(int i=0;i<A.size();i++){
        for(int j=0;j<B[0].size();j++){
            for(int k=0;k<A[0].size();k++){
                C[i][j]=(C[i][j]+A[i][k]*B[k][j])%mod;
            }
        }
    }
    return C;
}
mat qpow(mat &A,int n) //矩阵快速幂
{
    mat B(A.size(),vector<ll>(A[0].size()));
    for(int i=0;i<A.size();i++)
     for(int j=0;j<B.size();j++){
        if(i==j) B[i][j]=1;
        else B[i][j]=0;
    }
   //构造单位矩阵，相当普通的快速幂中的1
    while(n){
        if(n&1) B=mul(B,A);
        A=mul(A,A);
        n>>=1;
    }
    return B;
}
int main()
{
    int n;
    scanf("%d",&n);
    mat A{{1,1},{1,0}};  // 斐波拉契的常数矩阵。（构造方法可以自行百度，这里就不介绍了）
    A=qpow(A,n-1);
   cout<<A[0][0]<<endl;
    return 0;
}