【讨论_图论】DFS问题(一)
原问题(算法概论P99 3.22)Give an efficient algorithm that takes as input a directed acyclic graph G = {V, E}, and determines whether or not there is a vertex s ∈ V from which all other vertices are reachable.
简单理解问题的要求,即给出一个有向图G,判断G中是否存在一个点,使得这个点与任意其他点连通。
算法一
当然此处还是从最直接暴力的方法开始。首先对所有点进行遍历,然后对于所有点采用DFS,如果存在一个点的DFS搜索树包含所有点,那么这个点就是题目所求的点s。这种算法的缺点就是太过复杂,很明显在搜索过程中会出现很多重复的搜索,这也为算法的改进提供了理论基础。
算法二
在算法一中我们明确了问题所要求到的,是以某个点s ∈ V为根节点所形成的包含所有 V 中点的 DFS 树,如果找到了,那么就存在这样一个点s满足条件。
那么我们从答案出发,假设存在这样的DFS树,我们要怎么把它找出来呢?
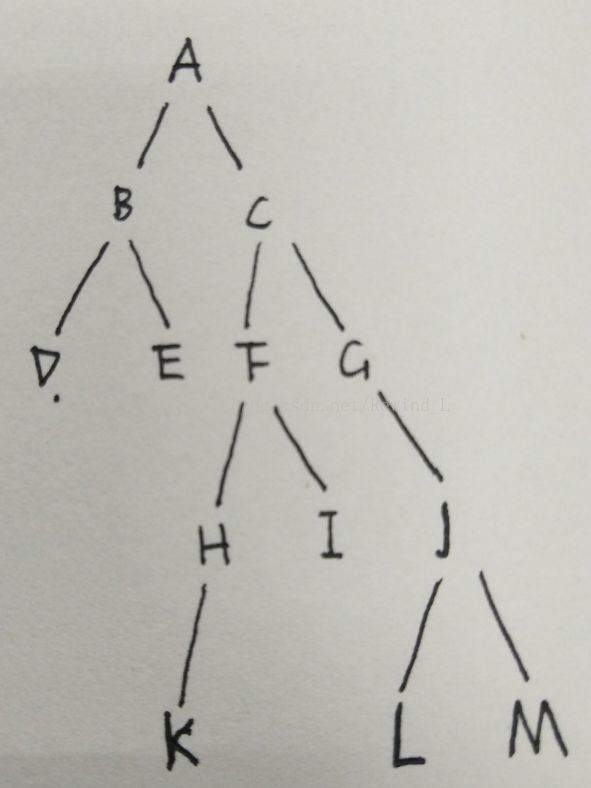
如下图所示:
假设V={A, B, C, D, E, F, G, H, I, J, K, L, M},图中就是以A为定点的 DFS 树,那么A即为所求点。现在如果有这样一颗树了,我们应该怎么去得到它呢?
这里提出一种想法,也就是利用DFS的思想,如果对于每个取到的顶点S1,我都把这个顶点S1当作答案DFS树的根节点进行DFS。如果经过了所有顶点,那么找到了答案;反之,我把以它为根节点的DFS树当作答案树的子数,那么此时相当于已经找到了答案DFS树的一部分。下一步要做的就是找出答案树剩余的部分,只需要对剩下的顶点选出一个S2继续进行DFS,如果S2的DFS树经过刚才取出的顶点S1,那么就相当于找到了更大一部分的答案树,将新增的部分填充上去,继续对剩下的点进行DFS,直到最后一个点。当然如果最后剩下的点已经无法与之前的DFS树建立联系了,则不存在这样一个点。
刚才的想法是从答案反推而来的,现在尝试从正面去推导这个算法。
依然从顶点集V中取出一点S1,并对集合V中的点进行DFS搜索,生成DFS搜索树T1,如果T1没有包含V中所有的点,那么我们可以得到一个结论:T1中所有的点都不是我们所要求的点S,因为它们不论谁进行DFS搜索都不能经过T1以外的点(DFS树的性质),那么所求的答案点只能在剩下的点中找。将T1中的点从V中剔除,得到新的子点集V1,从V1中随意取出一个点S2对【V1所有的点加上S1】进行DFS搜索,如果生成的DFS搜索树T1A能经过S1,那么将T1A和T1合并生成T2。如果T2能够包含V中所有点,那么S2即为所求点。反之继续将新增入DFS树的点从V1中剔除,生成更小的子集V2。对V2重复以上操作,直到能够找出包含V中所有店的DFS树(找到s)或者已经无法向DFS树中新增点(不存在s)为止。这样就完成了对一个图G的判断。
这里解释一下上述算法递归的过程中为什么新DFS树TkA只需要经过之前DFS树Tk的的根节点呢?我们直到如果答案点存在,那么它如果要有通路到达Tk中的所有结点,只需要检验它是否有到达其根节点Sk的通路即可【原因很简单,如果它能有到达Sk的通路,那么它一定能经过Sk的子节点;反之如果不存在到达Sk的通路,那么它已经被淘汰掉了】。这就是为什么只需要将之前树的根节点进行DFS的原因。
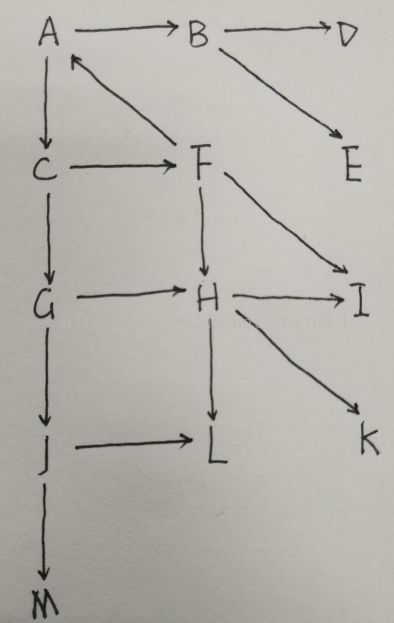
下面再举出一道实例:
对于这个图而言,V={A, B, C, D, E, F, G, H, I, J, K, L ,M}。现在开始我们的算法步骤。
①随机取出一个点H,从H开始进行DFS,得到的一个DFS搜索树T1(H, I, L, K)(这里只标注出顶点),那么去除这些顶点并加入H后得到V1 = {A, B, C, D, F, G, J, M,H};
②从V1中随机取点D,明显以D为根节点的DFS树D→E并不能包含①中根节点H,此点暂时淘汰;
从V1中继续随机取点G,此时对V1中的点进行DFS,以G点为根节点生成的DFS树为(G, J, M, H),合并①中的得到的搜索树生成T2(G, J, M, H, I, L, K),从V1中继续剔除DFS树中新增的点并加入G得到V2 = {A, B, C, D, E, G};
③从V2中随机取点A,此时可以看到:以A为顶点的DFS树已经包含了V2中所有的点,这样合并②中的T2,得到包含V中所有点的DFS树,这个树的根节点为A。明显点A是满足条件的(因为它是根节点)。
这样我们就求出了满足条件的点A。
总结:(1)这个算法避免了暴力搜索中的大量重复现象,保证了每个结点只会遍历一次,很大程度提高了效率,降低了复杂度;
(2)当然这个算法仍然有有待改进的地方:①过程略复杂;②随机取点在最坏的情况下仍然存在大量运算。