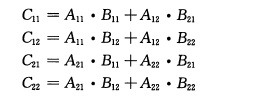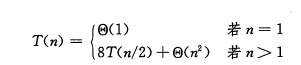分治策略之矩阵乘法的几种实现
欢迎关注,定期更新算法问题
今天介绍一下分治算法的一个典型例子——矩阵乘法
如果以前了解过矩阵,应该知道矩阵的乘法公式C(m,n)=A(m,k)*B(k,n),在这里我们只讨论方阵,假设A是n*n阶,B也是n*n阶,那么要计算乘积需要进行n^2个元素,看《算法导论》给出的伪码:
上边这个过程进行三次循环,每次循环执行n步,故花费时间是O(n^3),下边是代码实现:
void Squre_Multiplay(int A[][n],int B[][n],int C[][n])
{
int i,j;
for(i=0;i当然我们学习了分治算法后可以考虑能否利用递归来降低时间复杂度,先来看一个简单的分治算法:
假设A,B,C都是n*n阶,n是2的幂,乘法公式C=A*B,我们可以将这三个矩阵分别化成4个(n/2)*(n/2)阶的矩阵,即
然后可以将乘法公式写成4个递归式:
有了递归式就可以设计算法了,思路即是进行分解,求解,合并这几个步骤,将大矩阵化为4个小矩阵直到足够小,然后进行简单的二阶矩阵的计算,以下是《算法导论》上的伪码:
这段伪码理解起来很简单,但是实现起来比较复杂,因为它隐藏了一个重要的细节,即如何划分矩阵的问题,我们常规做法可能是新建几个新的矩阵,然后在从原矩阵特定位置赋值过来,但这样实现起来复杂并且很容易出错,这里本人利用下标来进行划分和计算,代码看起来清晰:
void Squre_Multiplay_recursive(int A[][n],int B[][n],int C[][n],int A_flag[],int B_flag[])
{
if(N==2)
{
C[A_flag[2]][B_flag[0]]=A[A_flag[2]][A_flag[0]]*B[B_flag[2]][B_flag[0]]+A[A_flag[2]][A_flag[1]]*B[B_flag[3]][B_flag[0]]+C[A_flag[2]][B_flag[0]];
C[A_flag[2]][B_flag[1]]=A[A_flag[2]][A_flag[0]]*B[B_flag[2]][B_flag[1]]+A[A_flag[2]][A_flag[1]]*B[B_flag[3]][B_flag[1]]+C[A_flag[2]][B_flag[1]];
C[A_flag[3]][B_flag[0]]=A[A_flag[3]][A_flag[0]]*B[B_flag[2]][B_flag[0]]+A[A_flag[3]][A_flag[1]]*B[B_flag[3]][B_flag[0]]+C[A_flag[3]][B_flag[0]];
C[A_flag[3]][B_flag[1]]=A[A_flag[3]][A_flag[0]]*B[B_flag[2]][B_flag[1]]+A[A_flag[3]][A_flag[1]]*B[B_flag[3]][B_flag[1]]+C[A_flag[3]][B_flag[1]];
}
else
{
// int one[4],two[4],three[4],four[4];
N=N/2;
cout<<"N value:"<上述算法运行时间的递归式:
通过求解,可以看出T(n)=O(n^3),与一般算法比较,并没有任何提高,反而增加了递归带来的开销。
下一篇介绍Strassen算法。
此篇全部源码如下:
#include
#define n 4
int N=n;
using namespace std;
void divide_array(int Array[][n],int flag[],int one[],int two[],int three[],int four[]);
//一般方法,时间复杂度为O(n^3),
void Squre_Multiplay(int A[][n],int B[][n],int C[][n]);
//普通分治算法,时间复杂度为O(n^2);
void Squre_Multiplay_recursive(int A[][n],int B[][n],int C[][n],int A_flag[],int B_flag[]);
//Stassen算法
int main()
{
int A[4][4]={1,2,3,4,1,2,3,4,1,2,3,4,1,2,3,4};
int B[4][4]={1,2,3,4,1,2,3,4,1,2,3,4,1,2,3,4};
int C[4][4]={0};
int A_flag[4]={0,3,0,3};
int B_flag[4]={0,3,0,3};
//Squre_Multiplay(A,B,C);
Squre_Multiplay_recursive(A,B,C,A_flag,B_flag);
for(int i=0;i